今回はデータ処理の一つの要である最小二乗法について学ぶ.
2つの変数間の関係が理論やモデル等で判明しているものを実験などで数値データを計測し,その係数を求めたい場合がある.
(例えば比例関係となるばね係数や,1次遅れ系の時定数の決定など)
例えば,比例関係であれば最小で2点の計測データから直線を1つ決めることができるが,計測データなどには「測定誤差」が含まれるため,より正確な係数を求めたい場合は必要なデータ数よりも多めに計測し,
それらを全て用いて最もよくあてはまる直線を決めると良いとされている.
この際,得られたデータ群をもとに客観的な方法で最もよく当てはまる関数の係数を決める方法の代表例が,最小二乗法である.
最小二乗法で決定できる関数の形は様々であり,工学でよく用いられる関数は1次関数の他に,2次関数,高次の多項式,指数関数,周期関数など,様々な場面で用いられる.
補間法が「制御点を滑らかな曲線で繋ぐ」ことで,制御点以外の関数値を求めるための手法であるのに対し, 最小二乗法は関数形をあらかじめ与えて,計測などにより得られた点群に最もよく当てはまる関数の係数を決定することを目的としており,その目的が大きく異なる.
いま,比例関係にある計測データとして $N$ 個の点群 ($x_i , y_i$) が得られたとする.
これらをもとに,もっともよく当てはまる関数(この例では直線)の係数を決定する方法が,最小二乗法である.
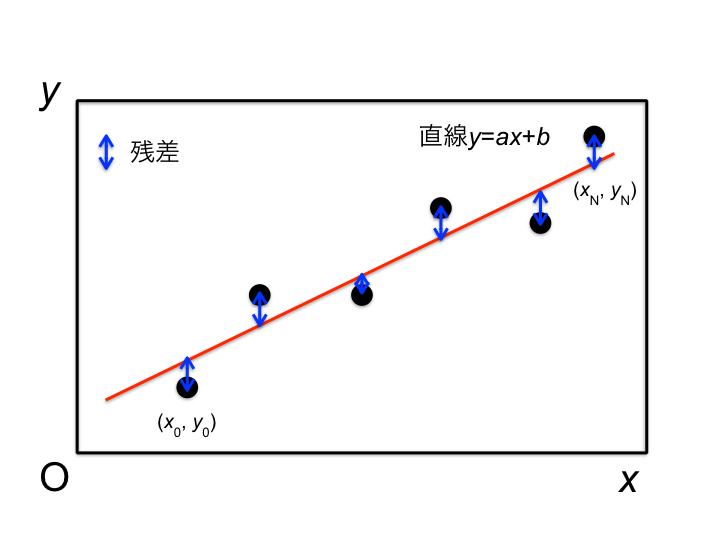
ここで,求めたい直線の式を $y=ax+b$ とする. 最小二乗法は,この $a, b$ の値を決定することが目的である.
直線と計測点との差(図中の青色矢印の部分)は,当てはめの度合いを示しており,残差と呼ばれる.
残差の合計が小さいほど,直線が点群の傾向をよく表していると言える.
各点における残差の値は正にも負にもなるので,そのまま足すと正負でキャンセルされてしまうためよろしくない.
そこで,残差の二乗の和を最小化することを考える.
残差の二乗和を $e$ とすると,$e$ は直線の傾きと切片 $(a,b)$ の関数となる.
以下の式で表される.
\begin{align} e(a,b) = \sum_{i=0}^{N-1}\left( y_i - (ax_i+b)\right)^2 \end{align}
$e$ は $ a, b$ の2次関数となるので,これが最小となる必要条件は,
\begin{align} \dfrac{\partial e}{\partial a} &= \sum_{i} 2\left( y_i - (ax_i+b)\right)(-x_i)=0 \notag\\ \dfrac{\partial e}{\partial b} &= \sum_{i} 2\left( y_i - (ax_i+b)\right)(-1)=0 \end{align}
である. 式を展開して整理すると,
\begin{align} \sum x_iy_i - a\sum x_i^2 - b\sum x_i=0 \notag\\ \sum y_i -a\sum x_i -b\sum 1=0 \end{align}
となる. これを$a,b$ に関する連立一次方程式として,$a, b$ について解くと
\begin{align} a &= \dfrac{\sum x_i\sum y_i - N\sum x_iy_i}{\left(\sum x_i\right)^2-N\sum x_i^2} \notag\\ b &= \dfrac{\sum x_iy_i\sum x_i - \sum x_i^2\sum y_i}{\left(\sum x_i\right)^2-N\sum x_i^2}\\ \end{align}
となる.
一見複雑に見えるが,それぞれ右辺は既知の点 $(x_i, y_i)$ の算術演算のみで表されるから,
簡単な代数計算により係数 $a, b$ が求まる.
計算のヒント:2乗の和と,和の2乗,の違いに注意.
ここでは,簡単な直線の例で示したが,2次関数や指数関数の最小二乗法も,残差を最小にするという考え方は同じである.
実験で,あるばねの変位と荷重に関するデータを得たとする.
以下のソースコード内の配列 x[], y[] はそれぞれバネの変位と荷重のデータである.
荷重と変位の間には比例関係があるとして,この比例係数(ばね定数)を求めよ.
参考ソースコード:
#include <iostream>
using namespace std;
double sum(double x[], int n)
/* 配列の合計 Σ を計算する関数 */
{
...
}
double sum2(double x[], int n)
/* 配列の2乗の合計 Σ を計算する関数 */
{
...
}
double inner_product(double x[], double y[], int n)
/* 二つの配列 x,y の内積を計算する関数 */
{
...
}
int main(void)
{
const int N = 10;
// あるばねにおける変位 x[mm] に対する荷重 y[N]
// 値を少し変化させてみて,各自で結果の変化を確認せよ.
// 動的配列を使用してもよい.
double x[N]={0, 1.1, 2.1, 3.0, 3.9, 5.0, 5.9, 7.1, 7.8, 8.9};
double y[N]={0, 2.4, 4.2, 5.7, 8.2, 9.2, 11.9, 14.0, 16.2, 17.4};
double a, b; // 一次関数の係数
// 以下にコードを記述
// 結果の出力
cout << "a = " << a << ", b = " << b << endl;
return 0;
}
実行例:(値が正しいとは限らない) a = 0.977565 b = 0.063278
ソースコード 153r000000-??-1.cpp を提出せよ.
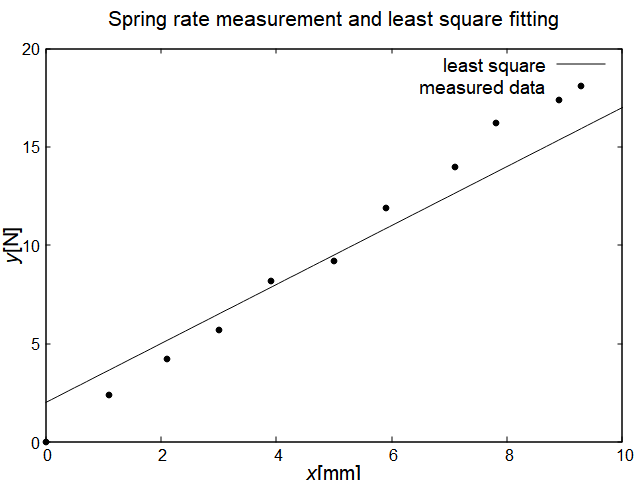
上記の計算コードを利用して,計算により以下のようなグラフを描け.
(この図では,直線と点群の最適なフィッティングができていない.)
グラフの作成には,Excelやグラフ作図ソフトを使用しても良い.または,gnuplotを使用することもできる.
参考までに,gnuplotで作図するテンプレート springrate.cpp を利用してもよい.
Gnuplotによる作図方法についての詳細は,本ページ末尾を参照.
ソースコード 153r000000-??-2.cpp およびグラフを画像形式(jpg, png, pdfなど)で保存したもの 153r000000-??-2.jpg, png, pdf を提出せよ.
プログラムによる計算やデータ処理の結果は,数値の羅列であるため,視覚的に表示することはとても重要となる.
それだけでなく,実験レポートや学術論文では,グラフの書式について一定のルールがある.
グラフの作成にあたっては,表計算ソフトではなく専用のツールを用いた方が容易であり,作業効率も良い.
gnuplot(グニュープロット,グヌー? ヌー?)は,昔から利用されているグラフを描くためのソフトウエアであり,無料で利用できる.
情報処理教室のPCには既にインストールされている.
自分のPCにインストールしたい場合は,公式サイト http://www.gnuplot.info/などからソース・バイナリをダウンロードできる.
Windows版のほかに,Mac OS版,Linux版などが利用できる.
Macで利用する場合は,各種設定や別途インストール(Homebrew, XQuartxなど)などの環境設定が必要となる.
授業ではまず情報処理教室のPCで試してみよう.
このように,簡単なコマンド入力で様々なグラフを描画することができる.
もちろん,関数形だけでなく,プログラムで出力した数値データのグラフ化もできる.
自作プログラムで何かの計算を行い,データファイルとして一旦 .txt や .csv ファイルに配列データなどを保存したのち,gnuplot を起動してコマンドからファイルを読み込ませる方法である.
この方法は,データファイルを保存しておくことができるため,データ処理プログラムとグラフ作成(可視化)過程を分けることができるメリットがある.
例えば,データファイル data.csv を出力したとする.
これは,さきのバネの試験データとする.
これをgnuplotで読み込んでグラフ化する.
(先頭の # の行は gnuplot ではコメントとして無視される.)
# Result by some experiment 0, 0 1.1, 2.4 2.1, 4.2 3.0, 5.7 3.9, 8.2 5.0, 9.2 5.9, 11.9 7.1, 14.0 7.8, 16.2 8.9, 17.4
まず,作業フォルダに,data.csv をダウンロードし,[File][Change Directory]で.csvファイルのあるフォルダを指定する.
次に,gnuplot の入力プロンプトで,以下のように打ち込んでみよう.
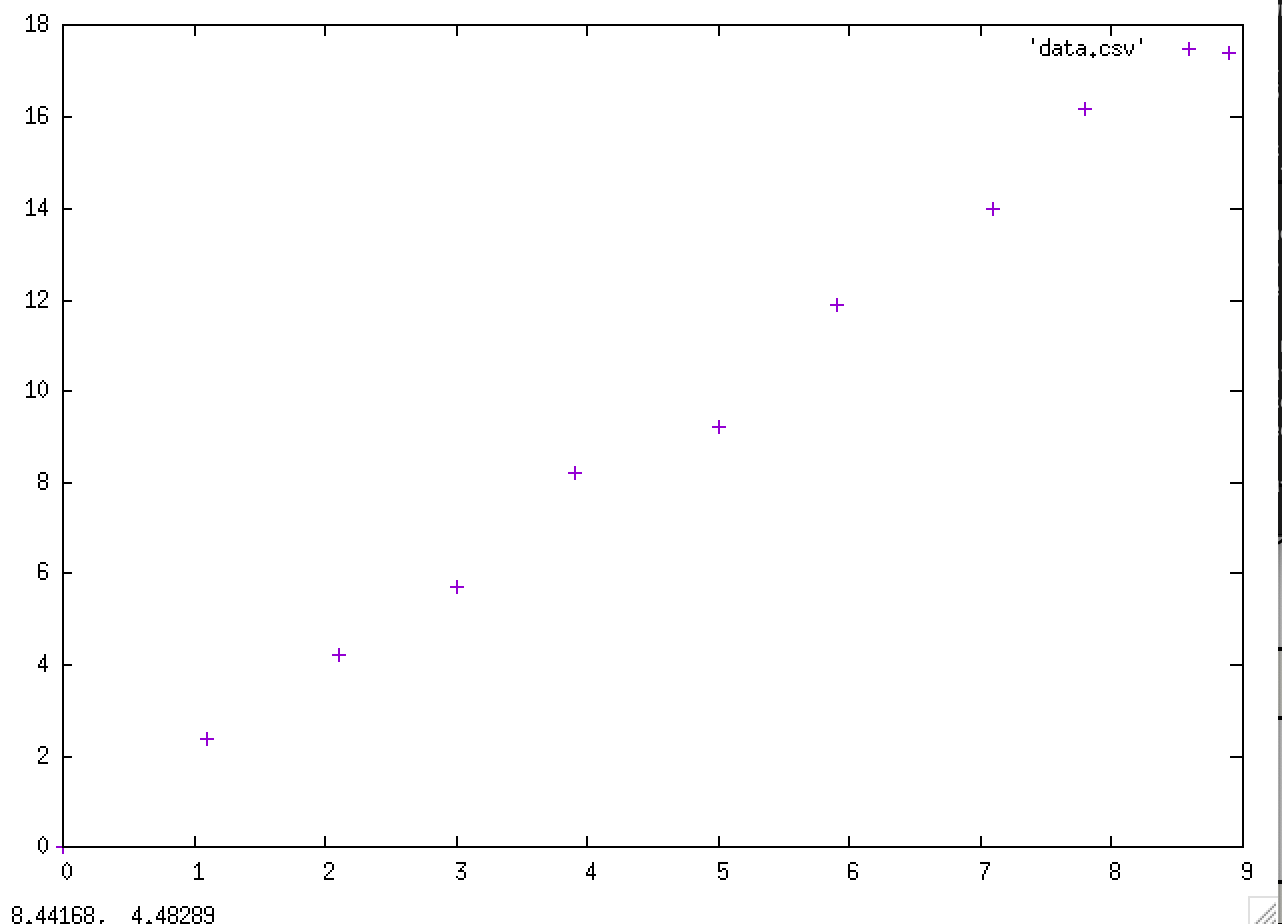
gnuplot> set datafile separator ',' gnuplot> plot 'data.csv'
たったこれだけで,.csv ファイル内に書かれた x,y 値の散布図グラフを書くことができた.
さらに,gnuplotに与えるコマンド(この2行)をあらかじめ .plt ファイル(例えば,ex1.plt)に保存しておくと,
gnuplot> load "ex1.plt"
とするだけで,プログラムのように呼び出すことができる.
set title 'Springrate experiment'
set xlabel '{/Consolas:Italic x}'
set ylabel '{/Consolas:Italic y}'
set xrange [0:10]
set yrange [0:20]
set datafile separator ','
set xzeroaxis linetype 3 linewidth 1 linecolor 'black'
set yzeroaxis linetype 3 linewidth 1 linecolor 'black'
plot 'data.csv' with points pt 7 linecolor 'black'
上記の.plt ファイル:dataread.plt
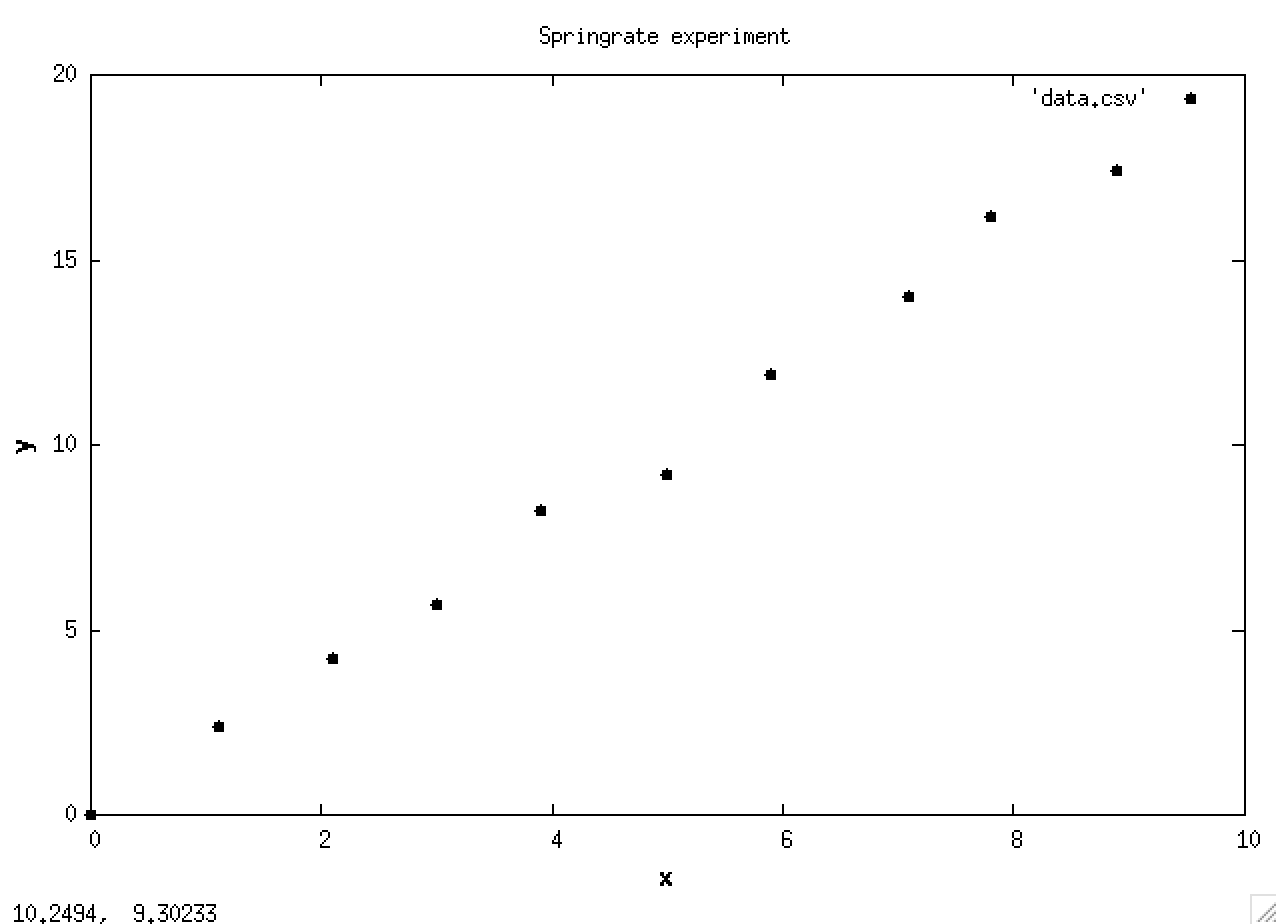
これらの設定は,最初に .plt ファイルに記述しておけば,データファイルを変えるだけで多くの同じ書式のグラフを作成でき,
gnuplot> load "dataread.plt"
のコマンド一発で,同じ設定のグラフが作成できる.
これ以外にも多種多様な種類のグラフが描けるので,詳しくは公式サイトのサンプルグラフやドキュメントを参照.
この方法はCプログラム中から直接 gnuplot を起動し,作図コマンドを直接送信することでグラフをリアルタイムに表示する方法である.
計算中のデータをダイレクトに可視化できるため,時間のかかる計算処理の途中結果を逐一チェックしたり,また,データ保存が必要なくグラフだけあれば良い場合に効率が良く,便利である.
Windows OS やUNIX には,あるプログラムから,外部の別のプログラムを呼び出し(実行し),データの受け渡しをする便利な「パイプ」と呼ばれる機能がある.
これを使えば,自分の作成したプログラムから gnuplot を実行し,計算データと各種設定を文字列として gnuplot に送信し,瞬時にグラフを描くことができる.
C言語で他のアプリケーション( = .exeファイル)を呼び出すには,popen()を使う.
見た目・使い方は,ファイル操作の fopen() に瓜二つである.
popen() で開いたパイプにfprintf()などを使って数値や文字を書き込めば,あたかもキーボードから入力しているかのように数値・文字を他のアプリケーションに送信できる.
// ptest.cpp
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
FILE *fp;
fp = popen("sayhello.exe", "w"); // sayhello.exeを実行し,パイプを開く
if(fp == NULL) {
printf("Pipe open error");
exit(1);
}
fprintf(fp, "Meiji Taro"); // sayhello.exe に文字列を送る
fflush(fp); // バッファをフラッシュ(書き出す)
pclose(fp); // 閉じる
return 0;
}
呼び出される sayhello.cpp のソースは以下のとおりである.
gcc等でコンパイルした場合は,実行ファイル名をa.exeからsayhello.exeに変更する.
// 文字列を受けとって,Hello と名前を出力する
#include <stdio.h>
int main(void)
{
char buf[100];
scanf("%s", buf);
printf("Hello %s!", buf);
return 0;
}
ptest.cppをコンパイルして実行すると,以下のように sayhello.exe に渡された文字列にHello が追加されて,画面に表示される.
実行例:Hello Meiji Taro
具体的には,Cプログラムから popen() 関数を使って gnuplot 実行ファイルを呼び出し(=実行),グラフ作画に必要なコマンドとデータをパイプ経由で送信する.
//
// 情報処理実習2 最小二乗法課題用テンプレート
//
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void draw_graph(
const double x[],
const double y[],
const int N,
const double a,
const double b
)
//
// gnuplot を呼び出して,散布図(x,y) および 直線 y=ax+b を描画する関数
//
{
// gnuplot の実行ファイルのパスを正しく設定しないと動作しない!
const char gp_cmd[] = "\"C:/Program Files/gnuplot/bin/gnuplot\" -persist"; // for windows(情報処理教室)
// const char gp_cmd[] = "/usr/local/bin/gnuplot -persist"; // for Mac(一例.)
FILE *fp;
fp = popen(gp_cmd, "w");
if(fp == NULL) {
printf("popen() error\n");
exit(1);
}
fprintf(fp, "set title 'Spring rate measurement and least square fitting'\n");
fprintf(fp, "set xrange [0 : 10.0]\n"); // x 軸の値の範囲
fprintf(fp, "set yrange [0 : 20.0]\n"); // y 軸の値の範囲
fprintf(fp, "set xlabel '{/Arial:Italic x}[mm]'\n"); // x 軸ラベル
fprintf(fp, "set ylabel '{/Arial:Italic y}[N]'\n"); // y 軸ラベル
// フォントの変更
fprintf(fp, "set title font 'Arial, 20'\n"); // タイトル
fprintf(fp, "set xlabel font 'Arial,16'\n"); // 横軸ラベル
fprintf(fp, "set ylabel font 'Arial,16'\n"); // 縦軸ラベル
fprintf(fp, "set key font 'Arial, 12'\n"); // 凡例
fprintf(fp, "set tics font 'Arial, 12'\n"); // 目盛
// plotコマンド用文字列バッファ
char buf[200];
snprintf(buf, 200, "plot (%lf*x+%lf) linecolor black title 'least square'", a, b); // 文字列bufに変数の値をセット
strcat(buf, ", '-' with points pt 7 linecolor black title 'measured data'\n");
fprintf(fp, buf); // gnuplotにplotコマンドを送信
// 散布図の座標値をgnuplotに送信
int i;
for(int i=0; i<N; i++) {
fprintf(fp,"%f\t%f\n", x[i], y[i]); // データの書き込み
}
fprintf(fp, "e\n");
fflush(fp);
pclose(fp);
}
int main(void)
{
// 計測されたデータ
const int N = 10;
double x[N]={0, 1.1, 2.1, 3.0, 3.9, 5.0, 5.9, 7.1, 7.8, 8.9};
double y[N]={0, 2.4, 4.2, 5.7, 8.2, 9.2, 11.9, 14.0, 16.2, 17.4};
// y = ax + b
// この a,b の値は,説明用の適当な値!
double a = 2.2;
double b = 1.5;
// *** ここで最小二乗法により a, b を計算 ***
// gnuplotでグラフを描く
draw_graph(x, y, N, a, b);
return 0;
}
popen() を _popen() に,(_ を追加)pclose() を _pclose() に,(_ を追加)const char gp_cmd[] = "/Applications/gnuplot.app/bin/gnuplot -persist";など