グラフィック表示処理やCADソフトウエアなどにおいては,物体や人物の表示に多くの座標データを扱う必要があるが,その全てを記憶しておくのは効率が悪い.
そこで,少ない数個の座標値などをもとに,その点を通る滑らかな曲線を得る手法でデータ数を削減している.
一般的に,少数の座標値からその他の複数の座標値を計算により求める手法を補間と呼ぶ.
(漢字の間違いに注意.「あいだ,間を補う」という意味で,○補間 ×補完)
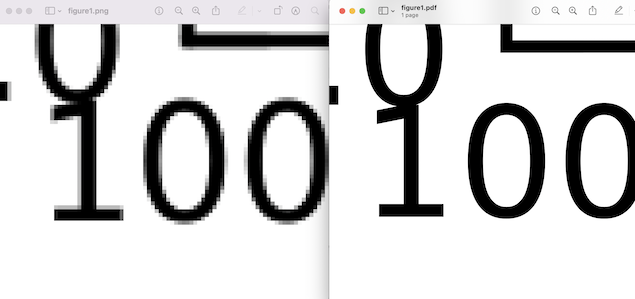
例えば,ワープロソフトのフォントのうち,アウトラインフォント(TrueTypeフォントなど)は,どれだけ拡大しても滑らかに表示できるが,ビットマップフォントは拡大するとギザギザが目立ってくる.
また,画像ファイル形式ではカメラで撮影した画像はビットマップ(bmp, jpeg,, png)であり,拡大すると画素,ドットが目立ってくるが,
一方,作図ソフトでベクター形式を用いて描いた図(svg, eps, PDF)は,制御点を補間により滑らかに繋いで表示するため,どれだけ拡大しても滑らかに表示できる.

補間では,制御点と呼ばれる既知の座標値数点を,何らかの関数(一般には低次の多項式)で滑らかに繋ぐ.
多項式は各次数の係数を決定すれば,関数の任意の値(=任意の $x$ に対する $y=f(x)$ の値)を計算することができる.
ところが,ここで学ぶ著名な補間法は,関数の係数を求めることなく,制御点の座標値から,他の任意の点の座標値を求める方法である.
補間法には多くの種類があるが,ここで学ぶ基本的な手法を以下に示す.
もっとも単純な補間法は線形補間である.
線形補間では,2点から関数を決定することができるため,その区間内外の任意の点に対する関数値を決定することができる.
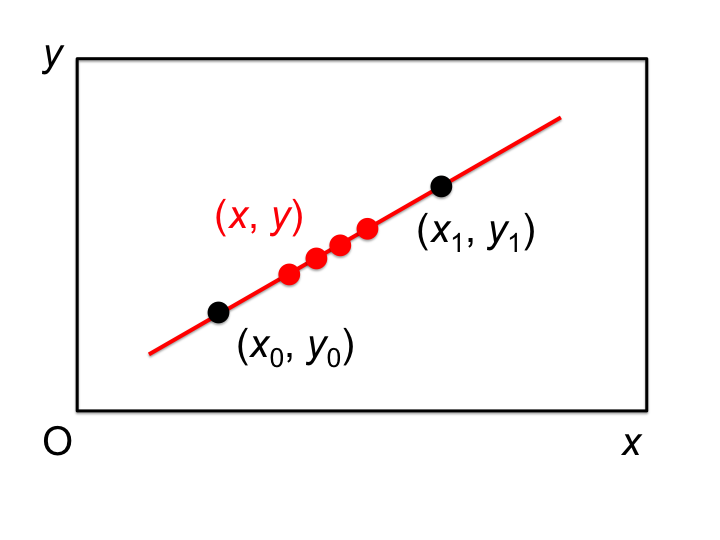
任意の2点に対する線形補間の式は以下のように表される. \begin{align} y - y_0 &= \dfrac{(y_1-y_0)}{(x_1-x_0)} (x-x_0) x_0\neq x_1 \end{align}
これを用いて,任意の $x$ にたいする $y$ を計算することができる.(注:$x_0, x_1, y_0, y_1$ はすべて定数)
より高次の関数についても,多項式の各係数を決めることにより関数が決定できる.
点群から補間により関数を決定すれば,任意の場所の関数値を計算できるが,どの位置の値を得るかにより内挿と外挿とに分けられる.
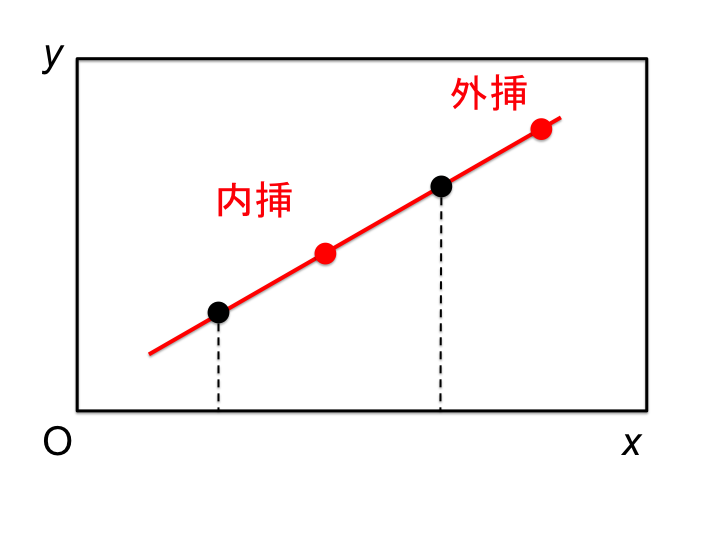
内挿 (interpolation)
外挿 (extrapolation)
一般的に,単純な補間法では,内挿に比べて外挿はその値の信頼性を担保することが難しいことが知られている.
線形補間では1次関数を使用するが,実用的には2次関数,3次関数など,より高次の関数を用いて補間を行う場合も多い.
一般に,独立した $N+1$ 個の座標値 $(x_0, y_0), (x_1, y_1), (x_2, y_2), ... , (x_N, y_N)$, ($x_i$は,すべて異なる) が与えられると,これらの点を全て通る $N$ 次多項式が決定できる.
例えば,多項式の係数 $y= a_0+ a_1 x+ a_2 x^2+ ...+ a_N x^N, a_N\neq 0$ による補間を考える.
$N+1$個の係数 $a_i$ をすべて決めれば,関数が一意に決まる.
関数の形が決まれば,あらゆる $x$ に対する $y$ の値が得られる.
この係数は,$N+1$ 元の連立1次方程式を解くことにより求めることができる.
例えば,$N=2$ の場合,3個の既知の点群 ($x_0, y_0$), ($x_1, y_1$), ($x_2, y_2$)を上式に代入することにより,以下の3本の方程式が得られる.
\begin{align*} a_0 + a_1 x_0 + a_2 x_0^2 = y_0\\ a_0 + a_1 x_1 + a_2 x_1^2 = y_1 \\ a_0 + a_1 x_2 + a_2 x_2^2 = y_2 \end{align*}
記号が多くあるが,$x_i, y_i$, $(i= 0,1,2)$ は既知の点群の座標値なので,ここでは未知の係数 $a_0, a_1,a_2$ を求める問題となる.
未知数が3個で,(独立な)方程式が3個あるので,係数 $a_i$ が一意に決まる.
補間に用いる点群の個数が増えるほど方程式の数が増えるため,逆行列や反復法を用いてまともに解くのは手間がかかる.
連立方程式を解くことなく,点群の座標値から $y = f(x)$ の値を得る手法が考案されており,ラグランジュ補間はその1つである.
この方法では,計算したい関数値$f(x)$を「数値的に」求めるだけであり,具体的に関数の形(=多項式の係数)を求めているわけではない.
例として,以下の図中に示された5つの点(制御点)を補間により滑らかに繋ぐ方法を考える.
即ち,この5点以外の任意の点の座標値 ($x,y$) の組み合わせを求めたいとする.
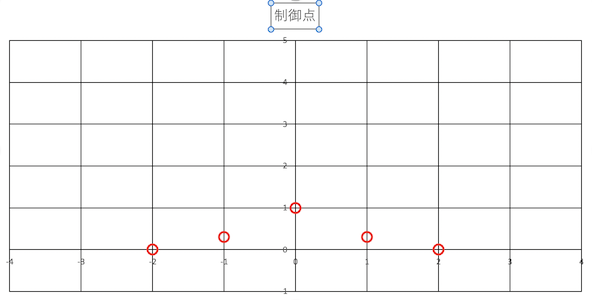
ラグランジュ補間法では,以下の式を用いて,$N+1$ 個の値 ($x_i, y_i$) を元に,任意の $x$ に対する $y=f(x)$ の値を計算することができる.
ここでは,$N=4$ である.
展開して書くと,以下の通りとなる.
\begin{align*} y &= f(x) \\ &= \frac{(x-x_1)(x-x_2)\cdot\cdot\cdot(x-x_N)}{(x_0-x_1)(x_0-x_2)\cdot\cdot\cdot(x_0-x_N)} y_0 \\ &+ \frac{(x-x_0)(x-x_2)\cdot\cdot\cdot(x-x_N)}{(x_1-x_0)(x_1-x_2)\cdot\cdot\cdot(x_1-x_N)} y_1 \\ &+ \cdot\cdot\cdot \\ &+ \frac{(x-x_0)(x-x_1)\cdot\cdot\cdot(x-x_{N-1})}{(x_N-x_0)(x_N-x_2)\cdot\cdot\cdot(x_{N}-x_{N-1})} y_N \\ \end{align*}
上の式を見ればわかる通り,既知の値を代入して計算するだけで,任意の $x$ にたいする値 $y$ が四則演算だけで計算できる.
一例として以下にラグランジ補間の関数例を示す.(三角印をクリックすると開く)
実習課題にあたっては,これらの関数がどのような処理をしているのかを充分に理解した後に,各自でプログラムを組み立てて使用すること.
この関数および main() 関数を含むサンプルソースコード Lagrange.cpp をダウンロードして使用しても良い.
#include<stdio.h>
struct Point2D // 点の座標を表す構造体
{
double x;
double y;
};
// データ数を表すグローバル変数
const int N = 5;
double Lagrange(const Point2D pnt[], const double x)
/*
* pnt : 点群を表す配列
* x : 求めたい x の値(点群以外の任意の値でもOK)
* 戻り値 : xに対応する関数値 y
*/
{
int i,j;
/* 計算用変数の初期化 */
double p, s = 0.0;
for (i = 0; i < N; i++) {
p = pnt[i].y; /* 積の計算 */
for (j = 0; j < N; j++) {
if (i != j) {
p *= (x - pnt[j].x) / (pnt[i].x - pnt[j].x);
}
}
s += p;
}
return s;
}
式で見ると複雑に見えるが,プログラムにすると意外とシンプルである.
実行例.値は正しいとは限らない x=? 0.1 (KBD入力) y= 0.27364 (出力)
出力例(画面またはファイルに出力)
-3.000000 , -0.300000
-2.900000 , -0.233357
-2.800000 , -0.178286
.
.
.
2.800000 , -0.178286
2.900000 , -0.233357
3.000000 , -0.300000
ヒント:まず,座標データをカンマ区切りテキストファイル(.csv)に出力する.
その後,.csvファイルをExcelで開き,グラフを作成する.
(ページの後方に手順の概略を記す.)
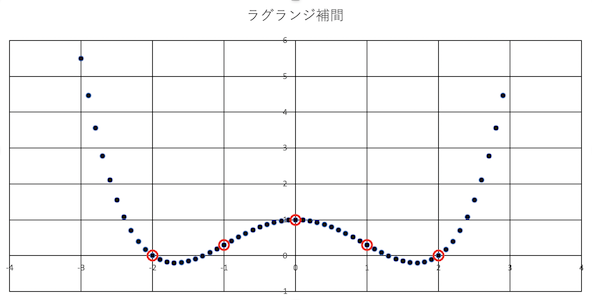
ラグランジュ補間では,制御点によっては意図しない形状になることがあり,
例えば,周期関数や指数関数,正規分布など,必ずしも多項式での近似がふさわしくない場合に発生する.
そこで,ラグランジュ補間のようにすべての点群を使って単一の関数を決定するのではなく,連続する数点のみを使って局所の関数(曲線)を決定し,かつ,その曲線を全体として滑らかに接続させる補間法が広く利用されている. その代表例がスプライン補間(スプライン曲線による補間)である.
「各区間」を近似する多項式にはいろいろ考えられるが,ここでは3次式を用いる「3次のスプライン補間,cubic spline」を行う.
\begin{align*} z_i(x) = p_i + q_i(x - x_i) + r_i(x - x_i)^2 + s_i(x - x_i)^3, \ \ \ i = 0,1, ... , n-1 \end{align*}
スプライン補間では,
ように,係数 $p_i,q_i,r_i,s_i$ を決める. (一般に,両端の2乗の係数は $r_0 = r_{n-1} = 0$ とする).
こちらも main() 関数を含むサンプルソースコード
をダウンロードして使用しても良い.
実習課題にあたっては,これらの関数がどのような処理をしているのかを充分に理解した後に,各自でプログラムを組み立てて使用すること.
#include <stdio.h>
struct Point2D
{
double x;
double y;
};
const int N = 5; /* データ個数 */
double spline(const Point2D pnt[], const double x)
/*
* スプライン補間関数
* pnt : 点群を表す配列
* x : 求めたい x の値(点群以外の任意の値でもOK)
* 戻り値 : xに対応する関数の値 y = f(x)
*/
{
int idx = -1, k;
double h[N-1], b[N-1], d[N-1], g[N-1], u[N-1], r[N];
int i;
for (i=1; i<N-1 && idx<0; i++) {
if (x < pnt[i].x )
idx = i - 1;
}
if (idx < 0)
idx = N-2;
for(i=0; i<N-1; i++) {
h[i] = pnt[i+1].x - pnt[i].x;
}
for (i=1; i<N-1; i++) {
b[i] = 2.0 * (h[i] + h[i-1]);
d[i] = 3.0 * ((pnt[i+1].y - pnt[i ].y) / h[i ]
- (pnt[i ].y - pnt[i-1].y) / h[i-1]);
}
g[1] = h[1] / b[1];
for (i=2; i<N-2; i++) {
g[i] = h[i] / (b[i] - h[i-1] * g[i-1]);
}
u[1] = d[1] / b[1];
for(i=2; i<N-1; i++) {
u[i] = (d[i]-h[i-1] * u[i-1]) / (b[i] - h[i-1] * g[i-1]);
}
if(idx > 1) {
k = idx;
} else {
k = 1;
}
r[0] = 0.0;
r[N-1] = 0.0;
r[N-2] = u[N-2];
for (i=N-3; i>=k; i--) {
r[i] = u[i] - g[i] * r[i+1];
}
double dx = x - pnt[idx].x;
double q = (pnt[idx+1].y - pnt[idx].y) / h[idx] - h[idx] * (r[idx+1] + 2.0 * r[idx]) / 3.0;
double s = (r[idx+1] - r[idx]) / (3.0 * h[idx]);
return pnt[idx].y + dx * (q + dx * (r[idx] + s * dx));
}
先ほどと同様,$x$ 値にたいする $y$ の値をスプライン補間で計算し,値を表示するプログラムを作成してみよう.
また,$-3.0<x<3.0$ の区間について 0.1 または 0.01 刻みで $y$ の値を計算し,グラフを作成してみよう.
注:使用中のPCやMacに,Microsoft Excelがインストールされていない場合は,無償の各種Office互換ソフト(Apache OpenOffice,LibreOfficeなど)や,Numbers などを用いても良い. その場合は,提出時に .xls 形式,まかは .xlsx 形式にエクスポートして提出すればOK.
計算した点群の座標を画面またはファイルに出力する.
ファイルの拡張子を .csv(カンマ区切りファイル)とする.
csv ファイルは「テキストファイル」で,各行に,カンマ区切りで x , y の座標値を格納する.
(.csvファイルの中身.値は正しいとは限らない) -3.00000 , -2.200000 -2.900000 , -0.300000 . . . 2.900000 , 2.300000 3.000000 , 2.200000
その他,Excelの詳しい操作方法,グラフの書き方については,Excelのヘルプを参照.
Windows 10(情報処理教室):リダイレクトによるcsvファイル生成と,Excelによるグラフ作成
Mac OS:リダイレクトによるcsvファイル生成と,Excelによるグラフ作成