微分方程式の数値解法2
Eular法では時間刻みを細かくしないと精度が低下する問題があった.
ここでは,大きな時間刻みでも正確な計算ができるより高度な方法を実験してみよう.
Runge-Kutta法
Eular(オイラー)法による数値積分は,勾配が大きな場面において,刻み幅を非常に小さく設定しないと計算誤差が大きくなることが予想される.
そこで,比較的大きな刻み幅(=少ない計算回数)でも精度のよいRunge–Kutta(ルンゲ・クッタ)法について学ぶ.
関数 $x=x(t)$ にたいして,微分方程式 $dx/dt = f(t, x)$ が定義されているとする.
$t$ の刻み幅を $h$ とし,
現在の時刻を $t_i$,次の時刻を $t_{i+1}= t_i+h$ とする.
Runge-Kutta法では,微小時間 $h$ 経過後の関数の値 $x_{i+1}$ を次のように算出する.
$x_{i+1}=x_i+k$, $k=(h/6) (k_0+2k_1+2k_2+k_3)$
ただし,係数 $k_0$ から $k_3$ はそれぞれ,
$k_0= f(t_i , x_i )$
$k_1= f(t_i+h/2, x_i+k_0 h/2)$
$k_2= f(t_i+h/2, x_i+k_1 h/2)$
$k_3= f(t_i+h , x_i+k_2 h )$
とする.
複雑な計算をしているように見えるが,$t$ や $x$ の異なる位置での微係数を計算し,重みを付けて次の時刻の関数値を計算しているだけである.
計算手順をまとめると,
- 初期値 $t_0$, $x_0$,時間刻み $h$ を設定.
- $k_0, k_1, k_2, k_3$ を計算.
- $k = (h/6)(k_0 + 2k_1 + 2k_2 + k_3$)を計算,
- $x_{i+1} = x_i + k$ より,時間刻み $h$ 後の値を算出
- 時刻を次の時間ステップ $t_{i+1} = t_i + h$ に進め,手順2に戻る.
となり,これをを繰り返すことによって任意の時刻まで値を順次求める(=数値積分する)ことができる.
ルンゲ・クッタ法以外にも,ルンゲ・クッタ・ギル法,ミルンの方法,アダムス法など,様々な手法が研究されている.
また,大規模な連立方程式を用いて安定的に計算を進める陰解法などがある.興味がある人は,各自で調べても良い.
参考:微分方程式の数値解法いろいろ(外部サイト)
2階微分方程式
機械工学で利用する微分方程式は,二階,もしくはそれ以上の高階の方程式が頻繁に登場する.
Runge-Kutta法は基本的に一階の微分方程式を解くための方法だが,少し工夫すれば,二階微分方程式を解くことができる.
具体的にどうするかと言うと,一階微分方程式を連立して解く方法を利用する.
いま,計算用に新しい変数 $z = dx/dt$ を導入する.(時間微分を「'」で表して,$x'= z$ とする)
これをもう一回微分すると, $x '' = z'$ が得られる.
これらを使って,
\begin{align*}
x' &= \frac{dx}{dt} = f(t, x, z)\\
z' &= \frac{d^2x}{dt^2} = g(t, x, z)
\end{align*}
の2つの方程式を同時に計算すれば良い.
具体的には,時間刻みを $h$ として,$x$, $z$ それぞれについて
\begin{align}
t_{i+1}&=t_i+h \notag\\
x_{i+1}&=x_i+k, \ \ \ \ k = (h/6) (k_0+2k_1+2k_2+k_3)\notag\\
z_{i+1}&=z_i+l, \ \ \ \ l = (h/6) (l_0+2l_1+2l_2+l_3)
\label{eqn:runge1}
\end{align}
となる計算を進める.
ただし
\begin{align}
k_0 &= f (t_i, x_i, z_i)\notag\\
l_0 &= g (t_i, x_i, z_i)\notag\\
k_1 &= f (t_i + h/2, x_i + k_0 h/2, z_i + l_0 h/2)\notag\\
l_1 &= g (t_i + h/2, x_i + k_0 h/2, z_i + l_0 h/2)\notag\\
k_2 &= f (t_i + h/2, x_i + k_1 h/2, z_i + l_1 h/2)\notag\\
l_2 &= g (t_i + h/2, x_i + k_1 h/2, z_i + l_1 h/2)\notag\\
k_3 &= f (t_i + h , x_i + k_2 h , z_i + l_2 h )\notag\\
l_3 &= g (t_i + h , x_i + k_2 h , z_i + l_2 h )
\label{eqn:runge2}
\end{align}
である.
Runge-Kutta法は Eular法に比べて計算式が増えており一見すると煩雑に見えるが,基本的にある時点での関数値に数点の勾配(=微係数)を重み付けして加算し,次の時刻の値を計算する考え方は同じである.
実習課題
以下の課題について,それぞれソースファイルおよび結果のグラフ(Excel, .jpeg, .png等)を提出すること.
課題1
前回の「課題1」の微分方程式を,Runge-Kutta法によって解き,Eular法による解と同じグラフに書いて,比較してみよう.
特に,時間刻み幅が大きな場合に,精度がどの程度向上するかを比較してみるとよい.
速度を $u=u(t)$ として,
$ u' = - bu^2 - au + g $
- $a,b,g$ は定数,例として
$a = 0.1~\mathrm{s^{-1}}$,
$b = 0.02~\mathrm{m^{-1}}$,
$g = 9.81~\mathrm{m/s^2}$
とする.任意に変更してよい.
- 初速は 時刻 $t=0~\mathrm{s}$ において $u(0)=0~\mathrm{m/s}$ とする.
この授業用の github 内の rktest.cpp を参照してもよい.
または,直リンク:rktest.cpp
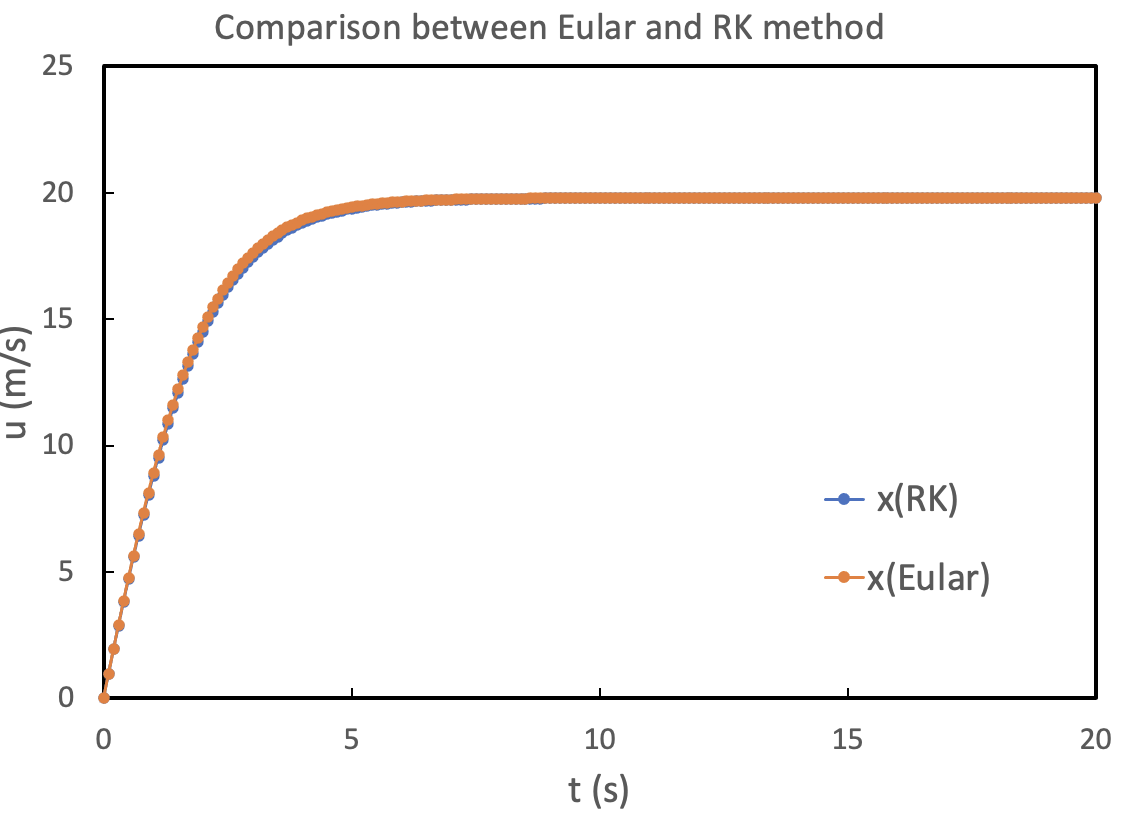 計算結果の比較.時間刻みは,0.1 s.
計算結果の比較.時間刻みは,0.1 s.
課題2
以下の関数は,ばね-マス-ダンパー系における運動方程式(2階の微分方程式)であり,定数次第で減衰振動となる.
このシミュレーションを行ってみよう.
以下の運動方程式について,様々な定数の下で,Runge-Kutta法を用いて数値的に解くことにより,振動の様子を比較しよう.
$x = x(t)$ は変位(位置)を表すものとし,$x'$, $x''$は速度,加速度である.
$x'' = - (c/m)x' - (k/m)x + u/m$
右辺の各項は,減衰項,ばね,外力に相当する.
定数については,例えば,
- $c/m = 0.02~\mathrm{N\cdot s/(m\cdot kg)}$
- $k/m=0.1~\mathrm{N/(m\cdot kg)}$
- $u/m=1~\mathrm{N/kg}$
としてみよう.
この値を用いて結果を確認したのち,値を変更すると結果がどう変化するか確かめてみよう.
初期条件は
- $x'(0) = 2~\mathrm{m/s}$ (初速)
- $x(t) = 0~\mathrm{m}$ (初期変位)
とし,計算時間は $t$ = 0~数百秒程度とする.
初期値や係数の値は変えてもかまわない.
ヒント:新しい変数 $z$ を用意し $z = x' = dx/dt$ とおくとき,
- $f(t, x, z) = x'$
- $g(t, x, z) = x''$
の形がそれぞれどうなるかを考えてみよう.
元の方程式の右辺が,関数 $g$ に相当します.
double f(double t, double x, double z)
{
return ????;
}
double g(double t, double x, double z)
{
return ????;
}
これらの関数を使用して,式\eqref{eqn:runge1}および式\eqref{eqn:runge2}を用いて $x$,$z$ の時間進行を計算してみよう.
参考:github 内の 2階の Runge-Kutta 法のサンプルコードrktest2_tmp.cppを使用しても良い.
このソースコードは未完成であるので,必要な箇所を追加,訂正すること.
以下に計算結果の一例を示す.この通りとならなくても良い.
減衰係数 $c$ の値を変えると減衰の程度が変化し,ばね定数 $k$ を変えると振動数が変化する.
また,初期条件の値も結果に影響するので,いろいろ値を変えて,3つの条件程度でシミュレーションを行ってみよう.
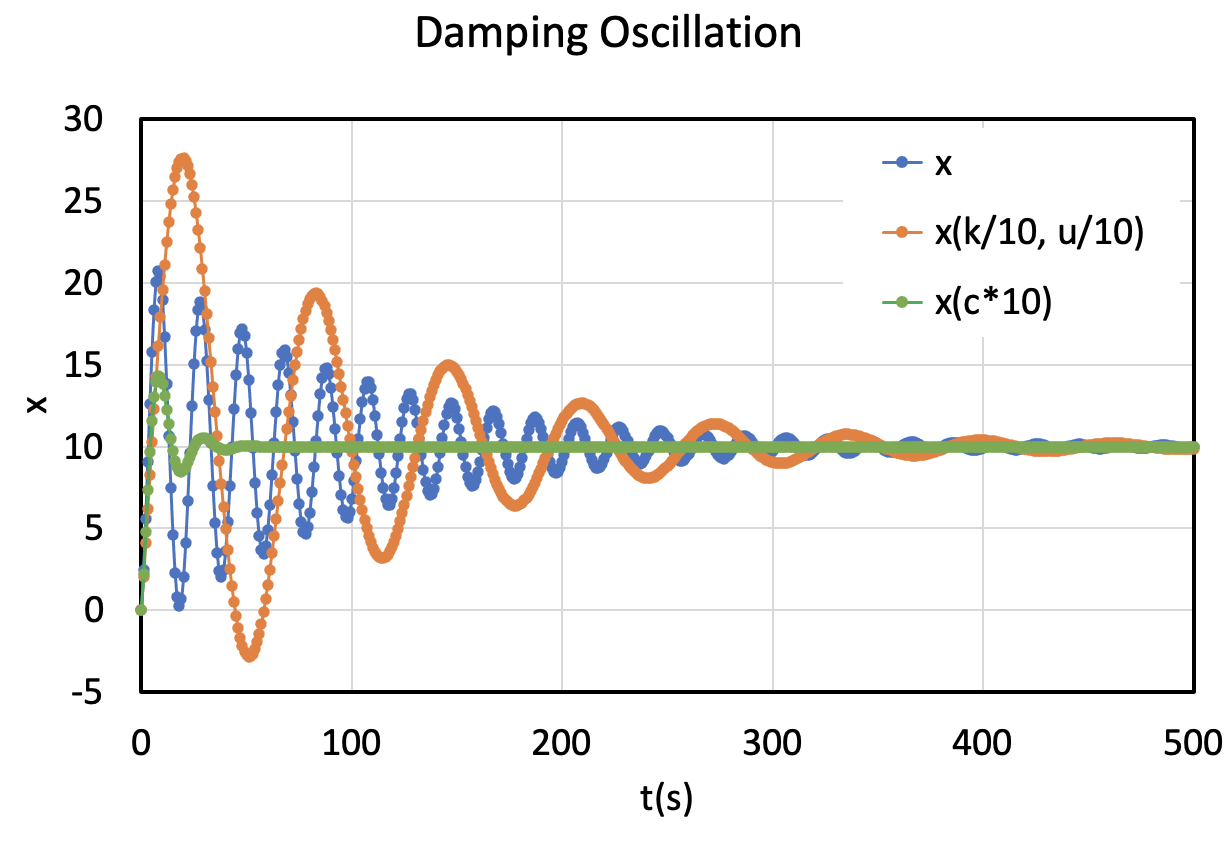
減衰振動の計算例,500秒間.ばね定数や減衰係数を変化させてみよう.

