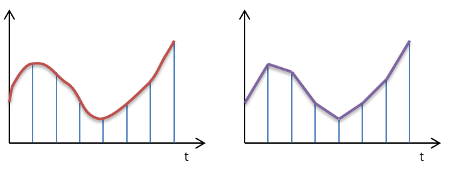
左:まず関数を区間に分割 右:各区間を台形で近似
機械工学の分野では,質点・剛体や連続体(流体)の運動や,材料の変形,熱物質移動,波動方程式など,多くの「微分方程式」が登場する.
これらの微分方程式のうち,ごく簡単な条件下では,紙と鉛筆を使って解ける場合(解析解という)があるが,一般的には解析解を得ることは容易ではない.
微分方程式には大きく分けて常微分方程式と偏微分方程式がある.
例えば,以下は二次元の熱エネルギーの移動を表す「熱伝導方程式」と呼ばれ,時間微分と空間微分を含む2階の偏微分方程式である.
\begin{align*} \rho c \dfrac{\partial T}{\partial t} = k\left(\dfrac{\partial^2 T}{\partial x^2} + \dfrac{\partial^2 T}{\partial y^2} \right) + \dot{q} \end{align*}
$x,y$ は空間座標,$t$ は時刻,$T$ は温度,$\rho$ は密度,$k$ は熱伝導率,$c$ は比熱,$\dot{q}$ は内部発熱である.
この式を解くことによって,例えばスマートフォンや家電製品の温度管理,エンジンの冷却,EVバッテリの熱管理や,建築物壁の断熱などの解析などができる.
(詳しくは熱力学,伝熱工学で学ぶ.)
熱の移動のほかにも,流体力学では流体の挙動,電気工学では電磁波・光波の進行(アンテナの設計やレンズの設計),機械力学では運動解析,材料力学では構造の強度や変形の計算,分子動力学による物性の推定など,工学では様々な多くの微分方程式が扱われる.
これら工学の応用分野においては,解析解が得られなくとも,ある一定の精度で数値解が得られれば良い場合が多い.
また,流体の支配方程式のように,そもそも解の存在の有無すら判明していない場合もある.
このような場面では,コンピュータを用いた微分方程式の解法 = 数値解法が有力なツールとなる.
ここで数値的に微分方程式を解くということは,現象を支配する方程式を満足する位置や温度,圧力,速度,加速度など物理量の時間変化や空間分布,またはそれらの両方を求めることに相当する.
これらはそれぞれ初期値問題,境界値問題と呼ばれている.
ここでは直感的にわかりやすい常微分方程式の初期値問題に対する数値計算法について学ぼう.
コンピュータによる数値積分は,計算機上では四則演算の繰り返し(面積の和)で近似的に表すことができる.
例えば「台形則」では,下図の通り,対象とする関数の曲線をある区間ごとに短冊状に区切り,
区切られた点を結んだ直線による台形の面積を足し合わせていく.

台形則では,区切りが粗いと直線と曲線の軌跡の違いが大きくなるが,区切りを充分に細かくすれば,
それぞれの台形の面積は元の関数の面積(積分)に近づくと考えられる.
一方で,計算機では非常に多くの小さな値の乗算・加算を繰り返すと,計算による誤差(丸め誤差・打切り誤差)が累積するため,短冊の刻みをやたら小さくすれば良いというわけではない.
こうした計算誤差を減らしつつ計算時間の短縮を実現するために,様々な計算手法(アルゴリズム)が提案・改良されている.
コンピュータによる計算において,非常に小さな数を多く足したり,非常に近い数同士を引き算すると,計算誤差が発生しやすい.
下の例では,1/NをN回加算している.当然,1になるはずであるが,処理系によっては計算誤差が発生する.
#include <stdio.h>
int main(void)
{
int N = 1000*1000*1000;
double dx = 1.0/N;
// 1/N を N回加算する.
double s=0.0;
for(int i=0; i<N; i++) {
s += dx;
}
printf("%.15lf\n", s); // 答えは当然 1.0000... となるべき
return 0;
}
出力例(処理系により異なる.)
0.999999992539933
まず,最も単純な Eular 法(オイラー法)を試そう.
いま,時刻 $t$ にたいして,関数 $f(t)$ は微分可能で,その導関数 $f'(t)$ が存在するとする.
微分方程式を差分にすると以下のように「近似」できる.
導関数は微小区間 $\Delta t$ の勾配を表すので,この微小区間を充分小さくとれば,誤差は減少する=真値に近づくと考えられる.
($\Delta t \rightarrow 0$ とすれば,微分の定義となる)
これを変形して
\begin{align*}
f(t+\Delta t) = f(t)+\Delta t \times f'(t)
\end{align*}
とする.
これをよく見ると,時刻 $t$ から微小時間 $\Delta t$ 経過後の関数の値 $f(t+\Delta t)$ は,
$f(t)$ に $\Delta t\times f'(t)$ を次々と足せば求められることを表している.
これがEular法の基本的な計算手順である.

アルゴリズムは大変シンプルである.
計算に必要な値は,初期値,導関数の値 $f'(t)$ と,時間刻み幅 $\Delta t$
(時間ステップと言う)である.
シミュレーションにあたっては,$t=0$ から何秒まで行うのか,刻み幅はどのくらいにするのかを適切に決めて計算する.
以下の微分方程式の数値解をオイラー法による数値積分で求め,グラフに表してみよう.
可能であれば,解析解と比較してみよう.(以下の微分方程式はいずれも簡単に解析解が求まる.)
以下,「微分方程式」,「初期条件」,「区間」とする
ヒント1:まず,(数学の)導関数を表す(C言語の)関数を定義せよ.
計算に必要な変数 $t, y$ または $x, y$ などの値を渡すと,導関数 $f'$ の値を返す関数である.
#include <stdio.h>
#include <math.h>
double f_prime(double t, double y) // 方程式によっては,渡された t, y を使用しない場合もある
{
return 2*t; // y'(t)=2t の場合
}
int main(void)
{
const double t_beg = 0.0; // 計算開始
const double t_end = 1.0; // 計算終了
const double dt = 0.1; // 時間刻み幅
double t = t_beg; // 時刻.初期値を設定
double y = 0.0; // yにも初期値を設定
// Eular法による時間進行
while(t<=t_end) {
printf("%lf, %lf\n", t, y); // 計算の途中結果を出力
y += dt * f_prime(t,y); // yを計算
t += dt; // 時刻tを進める
}
return 0;
}
以下の微分方程式をEular法により数値的に解き,グラフに表せ.
速度を $u$ として,
$\dfrac{du}{dt} = u'= -bu^2 - au + g $
これは,速度に比例する抵抗と,速度の2乗に比例する抵抗を受ける物体が,重力場中を運動(落下)する物体に関する運動方程式である.
(例:雨粒の落下)
この解の値(速度)は,時間の経過とともに「落下終端速度」と呼ばれる一定値に漸近してゆく.
速度を $u=u(t)$ とすると,加速度は$\dfrac{du}{dt}$と表されるから,正確に書くと
$\dfrac{du}{dt}= u'(t) = - bu^2(t)-au(t)+g$
となる.
手順:始めに, $u$ の値を引数として取り,微係数 $u'$ を返す関数 double du_dt(double u)を作る.
次に,時刻を0から開始して,時間刻みごとの $u$ を次々と計算,出力し,グラフに描く.
$t = 0 \sim 20~\mathrm{s}$ 程度について解き,値がほぼ一定値に漸近することを確認せよ.
また,時間の刻み幅を $1~\mathrm{s}$, $0.1~\mathrm{s}$ など変化さ,どのように解(曲線)が変化するか確かめよ.