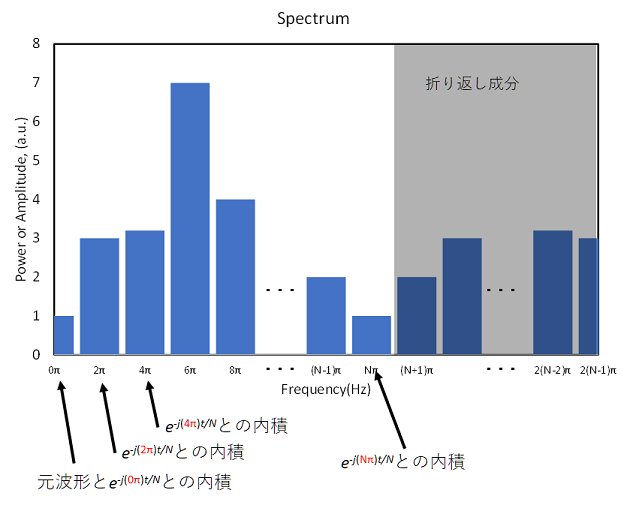
どの周波数の振動が,どのくらいの割合で含まれるかを表している.
後半の半分は折り返しのため,不要である.
離散フーリエ変換では,変換結果は一般的に複素数の配列となる.
変換後の関数の絶対値の2乗(=パワー)を縦軸に,周波数(または振動数)を横軸にとり,グラフに表したものを,パワースペクトルと呼び,どの周波数成分の波が,どのくらいの割合で含まれているかが一目でわかる.
以下に,パワースペクトル例を示す.
DFTにより計算した音声波形や画像などの実数データのパワースペクトルは,配列の前半と後半が折り返しとなる対称性の性質があり,後半の半分は不要である.
(この性質は,計算コードの検証に使うことができる.つまり,データが対称にならない場合は計算コードにバグがある可能性が高い.)

どの周波数の振動が,どのくらいの割合で含まれるかを表している.
後半の半分は折り返しのため,不要である.
離散フーリエ変換(DFT)は,データ数が大きくなると著しく計算負荷が高く(計算時間が データ数$N$ の2乗に比例)なるため,実用的には小さなデータ数しか計算できない問題があった.
1965年,James CooleyとJohn Tukeyにより,DFTの計算を劇的に高速化するアルゴリズムが開発された.
これは高速フーリエ変換(Fast Fourier Transform, FFT)と呼ばれる.
FFTは,データ数 $N$ が小さな素数の積(最も良いのは 2 の累乗の場合,$N$ = 2, 4, 8, 16, ..., 256 など)の場合,$N$ が大きくなっても計算時間がさほど増加せず($N\log N$ に比例),画像データなどの巨大なデータも短時間で変換できるため,実用性が高まった.
FFTの計算結果は,(計算誤差の範囲内で)DFTと一致する.
興味があれば,FFTのアルゴリズムや,C言語による実装についても調べ,実際に処理をしてみよう.
フーリエ変換,離散フーリエ変換,高速フーリエ変換の違いを理解しよう.
フーリエ変換に関する用語を,以下のようにまとめておく.
| 対象とする信号の長さ | 扱う周波数 | 特徴 | |
| フーリエ変換 | 無限に続く連続信号 | 無限の周波数の$\cos, \sin$の重ね合わせで表現 | 任意の連続関数に適用できるが,コンピュータでは無限個の値は扱えない |
| 離散フーリエ変換(DFT):今日の実習 | 有限長の$N$ 個の離散信号 | 周波数 $0\sim N/2$(ナイキスト周波数)の $\cos, \sin$の和で表現 | サンプリングされた有限長の信号を周波数に分解. この有限長の信号が,繰り返されることを前提とする |
| 高速(離散)フーリエ変換(FFT) | 同上 | 同上 | データ数 $N$ が小さな素数の累乗(特に $2^n$)で表される時,計算量(=計算時間)が劇的に少なくなる |
DFT と FFTの違いは,計算量(計算時間)にあり,計算結果は基本的に同じになるはずである.
DFT の計算時間は $N^2$ に比例するのに対し,FFTは $N \log_2(N/2)$ の計算時間しかかからないので,
特にデータ数 $N$ が大きくなるほど,FFTによる時間短縮効果は顕著となる.
実用的なスペクトル解析では FFT(高速フーリエ変換)が広く用いられているが,ここではフーリエ変換の原理を簡単に知るために DFT のコーディングについて学ぶ.
以下にDFTを行う関数の例を示す.
#include <stdio.h>
#include <complex>
#include <cmath>
using namespace std;
const double pi = 2.0*asin(1.0);
void dft(double in[], complex<double> out[], const int N)
// 離散フーリエ変換(DFT)
//
// in : 元データ(実数配列).
// out : 計算結果を格納.複素数配列. 呼び出しもとで確保する必要あり.
// N : in, outの要素数.複素数は(実部と虚部)で 1 個と数える
{
const double dt = 1.0 / 44100.0; // サンプリング周期(sec)を設定.44100 Hz の場合
// 出力用の配列を初期化
for(int i=0; i<N; i++) {
out[i] = complex<double>(0.0, 0.0); // ゼロに初期化
}
for(int f=0; f<N; f++) {
// 以下のループで 1個のF[omega]を計算する.
for(int t=0; t<N; t++) {
// 積分の中身の計算.
out[f] += in[t] * exp( complex<double>(0.0, -2.0 * pi * f * t/N) ) * dt;
}
}
}
グラフを作成する課題は,作成したC/C++ソースファイル(pythonは不可)に加えて,結果のグラフ (.png, .jpeg, .xlsxなど) を一緒に提出すること.
余力があれば,課題3にも取り組んでみよう.
課題3の提出は必須ではない.
以下を参考に,DFT演算を行うプログラムを作成し,
sin_waves(), square_wave() 関数で得られる波形を変換してみよう.
次に,変換結果(複素数配列)からパワーを計算し,ファイルに出力しグラフとして描いてみよう.
グラフの作成には,gnuplot, Excel, pythonなどを使用すると良い.
main() 関数内に実数配列を用意し,波形生成関数を呼び出して,配列に値をセットする.main() 関数内に複素数配列を用意し,dft() 関数に入力用配列,出力用配列と,データ数(整数)の,計3つの引数を渡す.
それぞれの波形のパワースペクトルはどのような形になったか,比較してみよう.
(信号に含まれる周波数に対応する位置に,0 でない値が出てくるはずである.)
// 処理手順のヒント
#include ...
int main(void)
{
const int N = ????; // データ数
double orig_data[N]; // 入力データ用配列
complex<double> dft_data[N]; // DFT変換後のデータ格納用配列
// 関数を呼び出して,orig_dataに値をセット
// dft関数を呼び出し
// dft_dataの絶対値の2乗を出力
return 0;
}
sin_waves(orig_data, N, 2, 4, 7);として呼び出し,DFTした結果を示す.
データ数を N=100,dt=1 としているため,各周波数に対応する行に 振幅×(N/2) の値が出てくる.
正確な振幅を求めたい場合は,計算結果を (N/2) で割れば良い.
各周波数に対するノルム(実部2+虚部2)の計算をすると,パワーの計算ができる.
i Re Im 0 0 0 1 0 0 2 0 -50 <- 周波数2のsinの振幅 3 0 0 4 107.5 0 <- 周波数4のcosの振幅 5 0 0 6 0 0 7 0 -150 <- 周波数7のsinの振幅 8 0 0 9 0 0 10 0 0 . . . (N/2+1 以降のデータは折り返しのため,本来は不要.) . . . 91 0 0 92 0 0 93 0 150 <- 周波数7のsinの振幅 の折り返し 94 0 0 95 0 0 96 107.5 0 <- 周波数4のcosの振幅 の折り返し 97 0 0 98 0 50 <- 周波数2のsinの振幅 の折り返し 99 0 0
Python のscipy には,フーリエ変換がパッケージとして用意されている.
グラフ作成のmatplotlib を用いて簡単に作画ができる.
# -*- coding: utf-8 -*-
#
# The original source code was obtained from https://docs.scipy.org/doc/scipy/tutorial/fft.html
#
from scipy.fft import fft, fftfreq
import numpy as np
import matplotlib.pyplot as plt
# Number of data points.
N = 100
# sampling interval in sec.
dt = 1.0/N
# generate waveform
x = np.linspace(0.0, N*dt, N, endpoint=False)
y = 1.0 *np.sin(2.0 * 2*np.pi * x) \
+ 2.15*np.cos(4.0 * 2*np.pi * x) \
+ 3.0 *np.sin(7.0 * 2*np.pi * x)
# Show original waveform
plt.plot(x, y)
plt.grid()
plt.show()
# Do FFT
yf = fft(y)
xf = fftfreq(N, dt)[:N//2]
# Show spectrum
plt.plot(xf, ( np.abs(yf[0:N//2])) )
plt.grid()
plt.show()
次の波形データファイルに様々な録音データがテキスト形式で含まれている.
いずれもデータ数 N=4096,サンプリング周波数 = 44100 Hz である.
まずこれらのファイルを右クリック,名前をつけて保存せよ.
以下の手順で,この波形を離散フーリエ変換し,パワースペクトルをグラフとして表示せよ.
dt = 1.0/44100.0 )とせよ.注意
// 処理手順のヒント
#include <stdio.h>
#include <stdlib.h>
#include <complex>
#include <cmath>
using namespace std;
const double pi = 2.0*asin(1.0);
// ここにDFT関数をコピー
void dft(double in[], complex out[], const int N)
...
int main(void)
{
const int N = 4096; // データ数
double orig_data[N]; // 入力データ用配列
complex<double> dft_data[N]; // DFT変換後のデータ格納用配列
const double sampling_freq = 44100; // サンプリング周波数
/////////////////////////////////////////////////////////
// 1. ファイルから配列 orig_data に値を読み込む
/////////////////////////////////////////////////////////
const char fname[] = "A_44100Hz.csv";
FILE* fp;
fp = fopen(...);
if(fp == NULL) {
...
}
for(...) {
fscanf(fp, "%lf", ...);
}
fclose(fp);
/////////////////////////////////////////////////////////
// 2. dft関数を呼び出し
/////////////////////////////////////////////////////////
dft(...);
/////////////////////////////////////////////////////////
// 3. パワー(絶対値の2乗)を出力. N/2まででOK
// csvファイルに出力すると良い.
/////////////////////////////////////////////////////////
FILE* fpo; // 出力用ファイルポインタ
fpo = fopen(...);
if(fpo == NULL) {
...
}
fprintf(fpo, "Freq(Hz), Power(-)\n");
// パワースペクトルの前半 0 から N/2+1 のみ出力.
// 周波数は,N/2+1 番目が,(サンプリング周波数)/2 となるように調整する.
for(int i=0; i<=N/2+1; i++) {
fprintf(fpo, "%lf, %lf \n", i*(sampling_freq/2)/(N/2+1), norm(dft_data[i]));
}
fclose(fpo);
return 0;
}
出力ファイルの例(周波数(Hz),パワーの順) Freq(Hz), Power(-) 0, 0.185407 10.769231, 0.19219 21.538462, 0.285634 32.307692, 0.218892 43.076923, 0.283933 53.846154, 0.793134 . . .
下の図のように横軸は周波数(Hz),縦軸はパワー(絶対値の2乗)の
(横軸も対数とする両対数グラフを使う場合もある.)
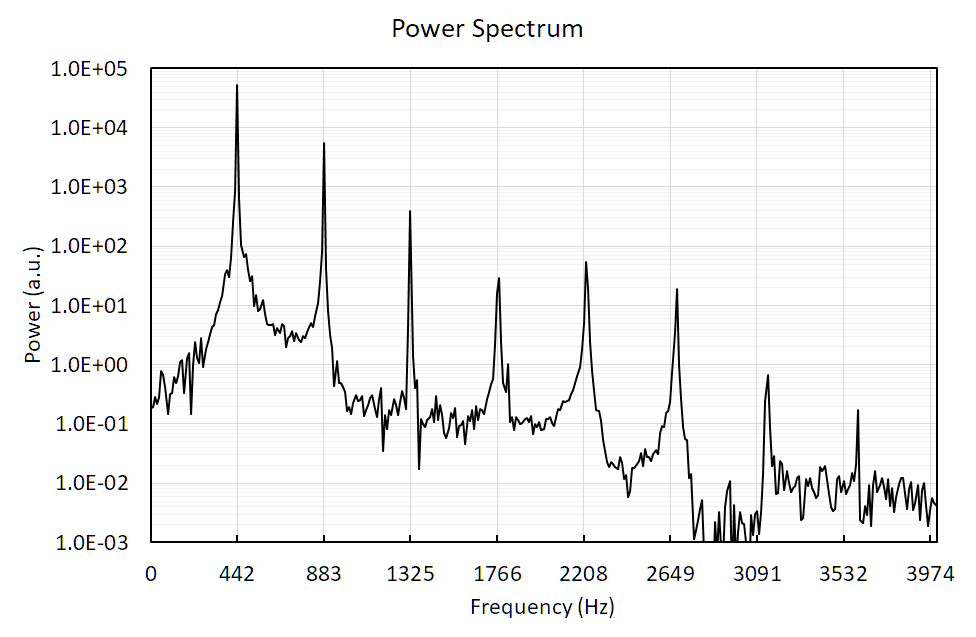
横軸は周波数の一部($0\sim4000$ Hzまで表示),縦軸はその波数の振幅の二乗(a.u.は,相対値の意).
基本周波数と,その整数倍の周波数に鋭いピークが現れる(倍音,三倍音.高調波,ハーモニックとも言う.)
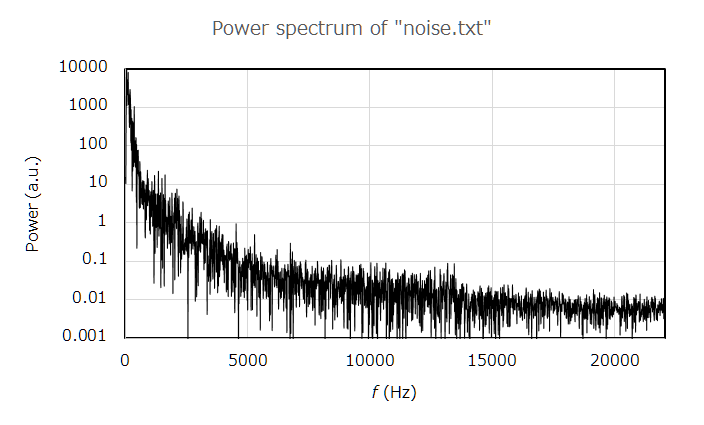
この例のように,パワーが周波数に反比例(=$1/f$に比例)するようなスペクトル特性を,ピンクノイズと呼ぶ.
また,周波数によらずパワーが一定となるようなノイズは,ホワイトノイズと呼ばれる.
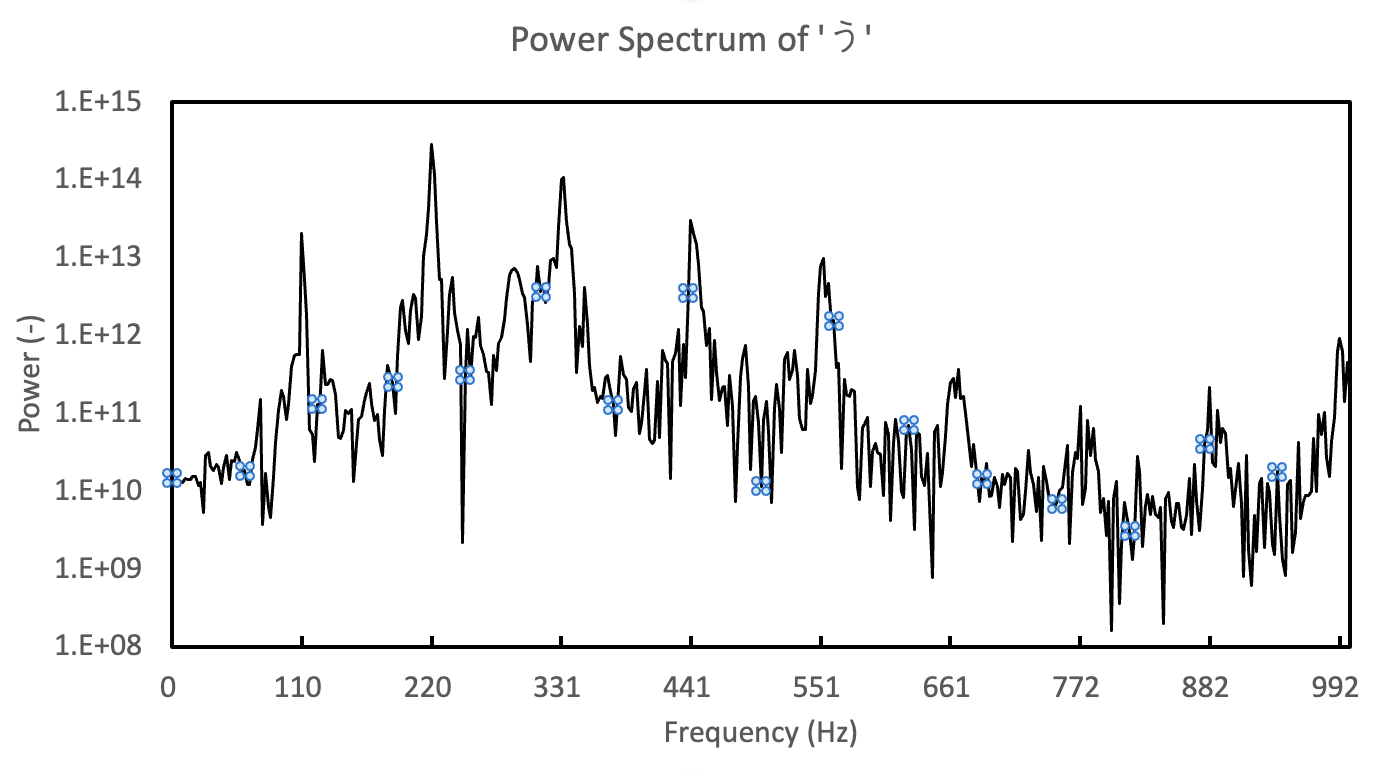
以下のファイルには発話時の音声信号波形が格納されている.
それぞれのパワースペクトルを計算し,グラフにしてみよう.何か違いが見えるでしょうか.
いずれもデータ数は N = 20000 個,サンプリング周波数は,44100Hz (dt=1/44100 sec)である.
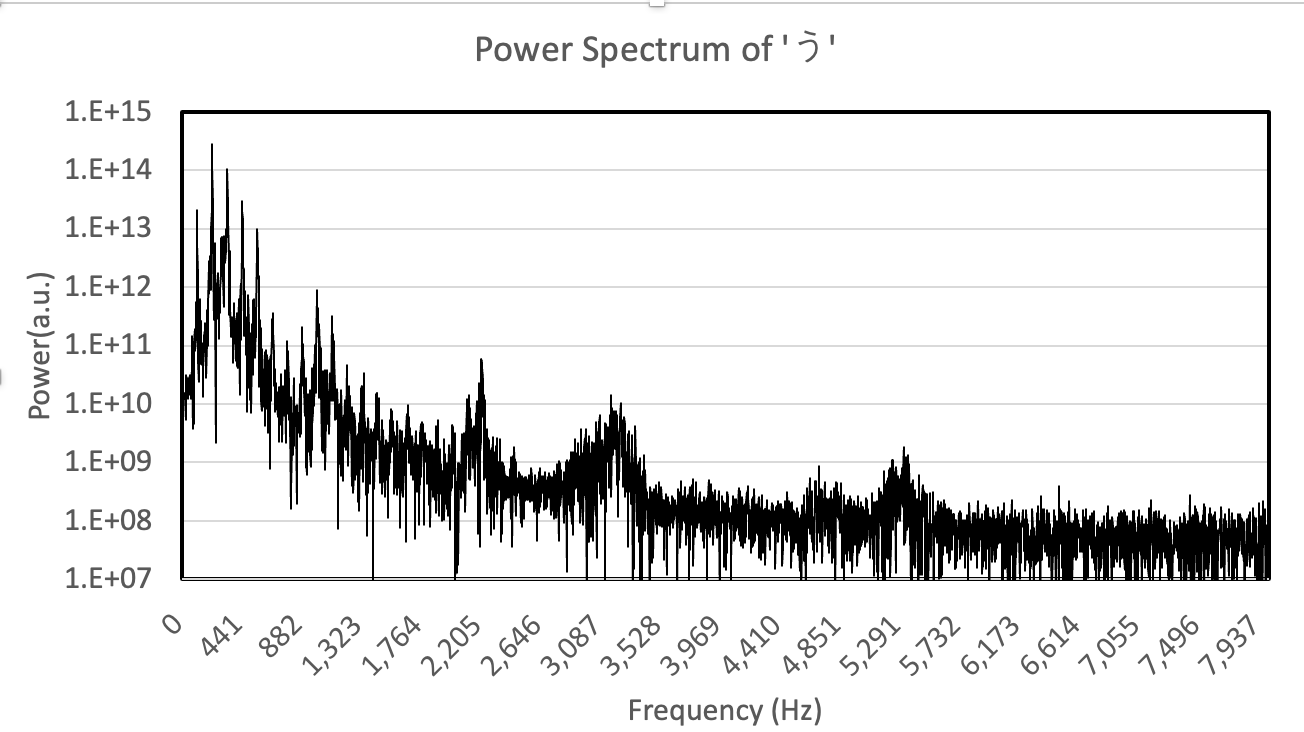
配列サイズが大きくなるので,配列宣言にstaticをつけよう.(stack overflow対策)
const int N = 20000;
static double orig_data[N];
static complex<double> dft_data[N];
コンパイル時に最適化オプション (-O2) をつけると,計算時間が短縮される場合がある.
逆に,コンパイル時間はやや増える.
c++ -O2 ????.cpp
人間の音声の周波数帯域は,せいぜい数 kHz 程度までである.
計算したスペクトルを全周波数について描く必要はなく,この例では上限周波数 $8\sim 10~\mathrm{kHz}$ 程度までで良い.