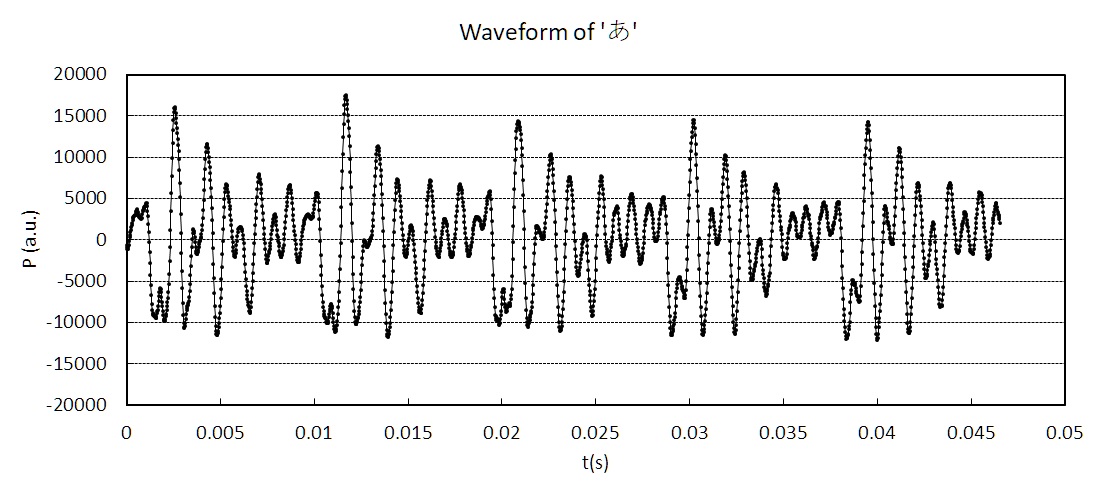
今回は,情報処理の応用の一つとして「信号処理」を扱う. 信号処理とは,実験などで得られた何らかの波形データを(数学に基づいた)方法で加工し,その特徴を抽出したり,雑音を軽減したり,必要な情報を抽出したりする手法の総称である. 広い意味では,2次元データである画像などの解析(画像処理と呼ばれ,顔認識,モザイク処理,色調変換や画像圧縮など)も信号処理に含まれる. ここでは簡単に1次元データの処理を考えよう.
ある波形データがあったとして,この波形から何か情報を抽出したり加工したいとする.
特に,周期的に変動する現象の解析は,工学のさまざまな分野において利用されている.
例えば,自動車や鉄道,船舶などの乗り物や,橋脚,建物,内燃機関など振動をなるべく抑制したい場合の解析に用いられる.
逆に楽器やスピーカー,通信アンテナなど所望の周波数でうまく振動・共振させたい場合も多くあり,その目的はさまざまである.

この例のように,実際の波形には何らかの周期性があることが予想されるが,単純な正弦波などには程遠く,それらが組み合わさった複雑な波形であるため,それ自体を眺めていてもよく分からない. そこで,信号にどのような周波数(または振動数)成分が,どのくらいの大きさ(振幅,またはその2乗のパワー)で含まれているかを数値的に解析することによって,その性質を把握することが出来る.
周波数,振動数は,どちらも単位はHzで似たようなものと考えらる.
周波数は,一般的に周期的に生ずる現象(交流電圧・電流,電波,電磁波,磁場,音など)を対象とした表現に用いられる.
「共振周波数」などの言葉の通り,積極的に振動・発振させ利用する意図を持った表現が多い.
これに対し,振動数は機械の構造物や機構の応答に用いられる表現でよく利用される.
また,原子や分子の運動に関しても振動数が用いられる.
「固有振動数」という言葉の通り,対象とする物理系の持つ特性を考える場合に用いられる.
周期的な波形は,様々な周波数の正弦波の和で表すことができると考えられる.
いま,ある区間 $[0, 2\pi]$ において時間変動する関数 $f(t)$ を,正弦関数,余弦関数($\sin, \cos$)の和で表すことを考える.
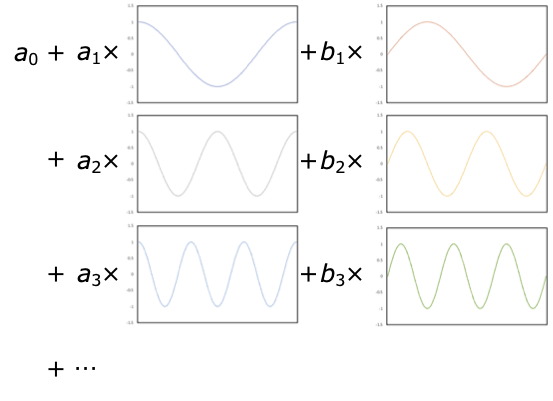
式で書くと,
\begin{align} f(t) &= \sum_{n=0}^\infty (a_n \cos nt + b_n \sin nt) \\ &= a_0 + \sum_{n=1}^\infty (a_n \cos nt + b_n \sin nt) \label{eqn:exp} \end{align}
とあらわせる.
この式は,いろいろな周波数の $\sin, \cos$ 波をある振幅で足してゆけば,任意の関数 $f$ を表すことができることを示している.
言い換えれば,任意の関数は,様々な周波数 $\omega$ にたいする振幅 $a_n, b_n$ に分解することができる.
では, $a_n, b_n$ の値は,どのような計算をすれば良いだろうか.
一つの方法として,三角関数の直交性を利用して,関数 $f$ と $\sin, \cos$ との内積を計算すれば, $a_n, b_n$ を取り出すことができる.
この性質をうまく利用して,各周波数に対応する振幅を求める方法がフーリエ変換である.
2次元のベクトルのなす角が90度の時,内積はゼロになります.
これを拡張して,一般にベクトルの内積がゼロとなる関係を「直交」という.
まず,三角関数の直交性を確認してみよう.
正弦関数において, \begin{align} \int_{0}^{2\pi} \sin mx \sin nx \ dx &= \frac{1}{2} \int_{0}^{2\pi}\cos(m-n)x\ dx - \frac{1}{2} \int_{0}^{2\pi}\cos(m+n)x\ dx \notag\\ &= 0 \ (m\neq n) \notag\\ &= \pi \ (m=n) \notag\\ \end{align} 同様に,余弦関数についても \begin{align} \int_{0}^{2\pi} \cos mx \cos nx \ dx &= 0 \ (m\neq n) \notag\\ &= \pi \ (m=n) \notag\\ \end{align} 正弦関数と余弦関数の積については \begin{align} \int_{0}^{2\pi} \sin mx \cos nx \ dx &= 0 \notag\\ \end{align} となる.
つまり,この積分値は $\sin$ 同士,$\cos$ 同士で,かつ,周期は一致する時のみ非ゼロとなる.
例えば,$n=2$,(周波数2の余弦波)の振幅 $a_2$ を求めたい場合は,式\eqref{eqn:exp}と$\cos 2t$ との積の積分を計算すると
\begin{align}
\int_{0}^{2\pi} f(t)(\cos 2t)dt &= \int_{0}^{2\pi} \left(a_0 + \sum_{n=1}^\infty (a_n \cos nt + b_n \sin nt)\right)(\cos 2t)\ dt\notag\\
&= \int_{0}^{2\pi} a_0 (\cos 2t) dt \notag\\
&+ \int_{0}^{2\pi} a_1 (\cos 1t)(\cos 2t) dt + \int_{0}^{2\pi} b_1 (\sin 1t)(\cos 2t) dt\notag\\
&+ \int_{0}^{2\pi} a_2 (\cos 2t)(\cos 2t) dt + \int_{0}^{2\pi} b_2 (\sin 2t)(\cos 2t) dt\notag\\
&+ \int_{0}^{2\pi} a_3 (\cos 3t)(\cos 2t) dt + \int_{0}^{2\pi} b_3 (\sin 3t)(\cos 2t) dt\notag\\
& + ...\notag\\
&= \int_{0}^{2\pi} a_2 (\cos 2t)(\cos 2t) dt = \pi\ a_2\notag
\end{align}
のように求められる.
同様に,$\sin 2t$ との内積の計算により,$b_2$ がもとまる.
このような考え方を一般化して,任意の関数を,様々な周波数の三角関数 $\sin, \cos$ の和で表すことができることが知られており,フーリエ変換と呼ばれる.
フーリエ変換(Fourier Transform)がどのような変換で,どのような性質かを理解しよう.
(フーリエ変換は,フランスの数学者 Joseph Fourier により,熱伝導を解析するために考案された手法である.)
時間 $t$ の関数 $f (t)$ があるとして,
この関数のフーリエ変換 $F(\omega)$ は以下のように定義される.
ここでは,オイラーの公式 $e^{j\omega t}=\cos\omega t + j\sin\omega t$ を使用している.
$j$ は虚数単位で,$j^2=-1$ である.
(工学の分野では,虚数単位に $i$ ではなく $j$ が使われることがある.$i$ は電流で使用されることが多いため?)
\begin{align} F(\omega) &= \int_{-\infty}^\infty f(t)\ \left(\cos(-\omega t) + j\sin(-\omega t)\right)\ dt \\ &= \int_{-\infty}^\infty f(t)\ e^{-j\omega t}\ dt \end{align} (注:複素数の指数関数は周期関数.)
$\omega~\mathrm{[rad/s]}$ は角周波数であり,周波数を $f~\mathrm{[Hz]}$ とすると,$\omega=2\pi f$の関係がある.(この $f$ は関数でなく周波数)
フーリエ変換は,時刻 $t$ の関数である $f$ を,周波数 $\omega$ の関数である $F$ に変換する.
$\omega$ の値を与えれば,$f$ 中の周波数 $\omega$ に相当する $\sin, \cos$ 成分の振幅がそれぞれ実部,虚部として得られる.
圧力や電圧など,連続的に変化する信号を計測により一定の時間間隔で取得し,離散的なデータ列に変換することを「サンプリング」や「標本化」と言う.
例えば,音声データや温度変化などの時系列データは,(時間軸)一次元の配列のデータとなる.
また,スマホやディジタルカメラなどで撮影した画像は,(空間軸)二次元の配列のデータとなる.
この測定の時間刻みのことをサンプリング間隔,またはサンプリング周期と呼び,単位は時間(sec, min等)となる.
サンプリング周期の逆数をサンプリング周波数と呼び,単位は $\mathrm{Hz}$ または $\mathrm{s^{-1}}$ である.
サンプリング周期は被測定量の変化よりも短く(つまり,対象が変化するよりも短時間で)する必要がある.
例1:24時間の外気温の変化をサンプリングするには 数分〜30分程度の時間間隔で十分であるが,エアコンや冷蔵庫の制御では 1分またはそれ以下の短い時間間隔で温度をサンプリングする必要がある.
例2:音声録音では一般的に 44.1kHz(=44100 Hz,つまり1秒間に44100回のサンプリング)が使用されており,これ以外にも 48kHz, 96kHz(ハイレゾリューション)などが利用されている.
例3:動画撮影のサンプリング周波数(Frames per second, fpsと呼ばれる)は一般に 24 Hz, 30 Hz 程度であるが,最近のスマートフォンの高速モードでは 240 Hz 程度,さらに産業用の高速度カメラでは数千Hz〜10億Hz以上のものがある.
サンプリング速度について詳しく知りたい場合は,標本化定理,ナイキスト周波数を参照.
いま,サンプリングする時間間隔を $\Delta t$ とすれば,データ配列の 0 番目には $f(0)$,1番目には $f(\Delta t)$,2番目には $f(2\Delta t)$・・・,といった計測データが順次入る.
コンピュータによるデータ処理では,必ず有限区間の離散化されたデータを対象とする.
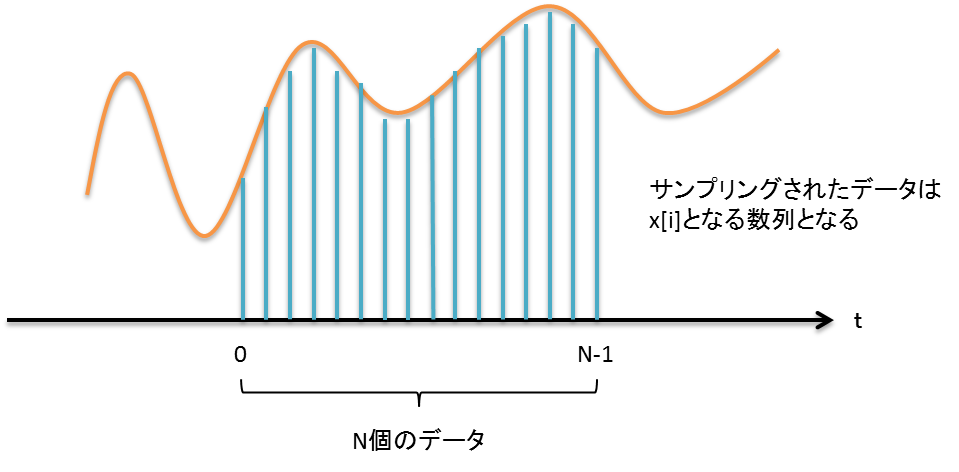
フーリエ変換の式は,連続である関数に対して定義されるが,一方で,計算機上で表現できるデータは有限長,かつ,サンプリングされた有限個の離散データである.
離散的なデータに対してのフーリエ変換は 離散フーリエ変換(Discrete Fourier Transform, DFT)と呼ばれ,コンピュータで計算できるのはこのDFTである.
ここでは,連続関数をサンプリングした有限個の離散データをC言語の配列風に d[t] とする.
(f[t] とすると周波数 f とまぎらわしいので,d[t]とした.以降,f は周波数を表すものとする.)
離散データ d[0], d[1], ... d[N-1] にたいする離散フーリエ変換は,以下のようにあらわされる.
$\omega = 2\pi f$ 置き換えているだけで,以下の二つの式は同一である.
\begin{align}
F[\omega] &= \sum_{t=0}^{N-1} \mathrm{d[t]}\ e^{-j\ (\omega\frac{t}{N}) }\ \Delta t \\
F[f] &= \sum_{t=0}^{N-1} \mathrm{d[t]}\ e^{-j\ (2\pi f\frac{t}{N}) }\ \Delta t \label{eqn:dft}
\end{align}
$F[\omega],F[f]$が,フーリエ変換後の関数(有限個の複素数配列)である.
右辺の指数関数の部分$e^{-j\ 2\pi f\frac{t}{N}}$は,$f = 1,2,3,...$ ($\omega = 2\pi, 4\pi, 6\pi$, ...) と増加するにつれ,周波数が増加する周期関数となる.
即ち,離散フーリエ変換は,いろいろな周波数 $f$ = 1, 2, 3, ... の余弦波・正弦波と,元の波形との内積により計算できる.
例えば,$f=1$ ($\omega=2\pi$) とすれば,元波形と1周期分の余弦波(実部)+正弦波(虚部)との内積が計算でき,その結果の実部・虚部がそれぞれ式$\eqref{eqn:exp}$ $a_1$,$b_1$ (の定数倍)となる.
同様に,$f = 2,3$ ($\omega=4\pi,6\pi$) とすれば,それぞれ2周期分,3周期分の余弦波+正弦波と元波形との内積が計算でき,それぞれ $a_2, b_2$,$a_3, b_3$ が計算できる.
C言語の組み込み型には,複素数型は存在しないため,C++ 標準テンプレートライブラリ(STL)の複素数クラス complex 型を用いる.
複素数型の定義には,実部・虚部を表す変数の型をあわせて指定する.(テンプレート機能)
このクラスライブラリには,実部・虚部を格納するメンバ変数だけでなく,複素数に関連する演算(四則演算,絶対値,指数関数など)が定義されているため,簡単に利用できとても便利である.
ここでは,複素数を $z=x+jy$ とする.
$x,y$ は実数である.$j$ は虚数単位で,$j^2=-1$ である.
数学では虚数単位として $i$ が使われるが,工学では電流$i$との混同を避けるため $j$ が使われることも多い.
complexの使用例#include <iostream>
#include <complex>
using namespace std;
int main(void)
{
complex<double> z1, z2; // 実部と虚部が double 型である複素数型変数の定義
// 実部・虚部を一括で代入
z1 = complex<double>(0.2, 1.0);
// 実部・虚部をそれぞれ個別に代入
z2.real(1.6);
z2.imag(-2.3);
// 複素数を表示
cout << "z1 = " << z1 << endl;
cout << "z2 = " << z2 << endl;
// 実部,虚部を別々に表示
cout << "Re{z1} = " << z1.real() << endl;
cout << "Im{z1} = " << z1.imag() << endl;
// 四則演算
cout << "z1 + z2 = " << z1 + z2 << endl;
cout << "z1 - z2 = " << z1 - z2 << endl;
cout << "z1 * z2 = " << z1 * z2 << endl;
cout << "z1 / z2 = " << z1 / z2 << endl;
// 共役複素数 conj()
cout << "conj(z1) = " << conj(z1) << endl;
// 絶対値 abs()
cout << "abs(z1) = " << abs(z1) << endl;
// ノルム(絶対値の2乗) norm()
cout << "norm(z1) = " << norm(z1) << endl;
// 偏角 arg()
cout << "arg(z1) = " << arg(z1) << endl;
// 指数関数 exp()
cout << "exp(z1) = " << exp(z1) << endl;
// 累乗 pow()
int n = 10;
cout << "pow(z1, " << n << ") = " << pow(z1, n) << endl;
}
z1, z2 の値を変更して,計算結果が変化すること,および,正しいことを確認せよ.次に,複素数型の「配列」を使用する練習をしてみよう.
// 複素数型の配列の宣言と使用例
#include <complex>
#include <stdio.h>
#include <math.h>
using namespace std;
const double pi = 2.0*asin(1.0);
int main(void)
{
const int N = 10;
complex<double> z; // 複素数型の変数
complex<double> y[N]; // 複素数型の配列.
// static complex<double> y[N]; // 複素数型の配列. Nが数千以上の場合,staticをつけてヒープメモリを使用する必要がある.
int i;
for(i=0; i<N; i++) {
// ヒント:2.0*pi*i/N は,i が 0 から N まで変化すると,0 から 2π まで変化する.
z = complex<double> (0.0, 2.0*pi*i/N); // 1周期分の純虚数
y[i] = exp(z); // 複素数の指数関数
printf("%lf, %lf\n", y[i].real(), y[i].imag()); // 表示
}
return 0;
}
複素数の宣言を書くと文字数が多く煩雑になる傾向があるので,以下のように typedef を用いて型名に別名を設定すると,少し簡単になる.
typedef 「既存の型名」 「別名」 の順に宣言する.
typedef complex<double> dcmpx;
int main()
{
dcmpx z1, z2; // 複素数型変数の宣言
z1 = dcomx (1.0, 2.0);
...
}また,最近では using 記法を用いて同様の設定ができる.
using 「別名」 = 「既存の型名」 の順に宣言する.
using dcmpx = complex<double>;
int main()
{
dcmpx z1, z2; /* 複素数型変数の宣言 */
z1 = dcomx (1.0, 2.0);
...
}
上記のサンプルソースコードを用いて,純虚数 $z = 0j \sim 2\pi j$ ($j$は虚数単位)までの区間を100分割し,
その指数関数 $y = \exp(z)$ の値を求め,図示したい.
複素数用のライブラリの exp() 関数を利用し,実部,虚部をそれぞれカンマ区切りファイル(csvファイル)に出力し,
実行例(.csvファイルの中身) real part, imaginary part 1.000000, 0.000000 0.998027, 0.062791 0.992115, 0.125333 ... 0.992115, -0.125333 0.998027, -0.062791
三角関数の直交性を確かめるために,以下の手順で上式を計算してみよう.積分区間は$0\sim 2\pi$とする.
まず,要素数が等しい2つの配列の内積を計算する関数の複素数バージョンを作成しよう.
戻り値も複素数となる.
#include<complex>
// 内積を計算する関数(複素数ver)
complex<double> inner_product(complex<double> a[], complex<double> b[], int N)
{
...
}
次に,上記関数の動作チェックのため,複素数配列を2つ用意し,実部または虚部に様々な周波数の正弦波・余弦波などの値を設定し,内積を計算して直交性を確認せよ.
f1, f2等しい周波数,および異なる周波数を設定して,その内積を比較しよう.
(計算誤差に起因して厳密にはゼロにはならないかもしれないが,10-10などの非常に小さな値になればOK.
#include <stdio.h>
#include <complex>
using namespace std;
const double pi = 2.0*asin(1.0);
// 内積を計算する関数(複素数ver)
complex<double> inner_product(complex<double> a[], complex<double> b[], int N)
{
...
}
int main(void)
{
const int N = 100;
int i;
complex<double> a[N], b[N];
// ここを色々変えてみる.scanfでKBD入力にするとよい.
double f1 = 3;
double f2 = 4;
// initialize array
for(i=0; i<N; i++) {
a[i] = complex<double>( sin( f1 * 2.0*pi*i/N), 0.0); // 実部にf1周期分の正弦波,虚部は0
b[i] = complex<double>( sin( f2 * 2.0*pi*i/N), 0.0); // 実部にf2周期分の正弦波,虚部は0
}
complex<double> ret = inner_product(a, b, N);
printf("%lf, %lf\n", ret.real(), ret.imag()); // 表示
}
フーリエ変換のプログラミングの準備として,以下に挙げる波形を生成する関数を作成,動作確認せよ.
得られた波形の形状をグラフにして確認すること.
グラフの提出は不要である.
main関数を含むファイルは153R000000-??-1.cpp とする.
以下,特に指定が無い限り
x は信号データの格納された実数型配列,
n は配列の要素数(データ個数)
である.
どのような値の n が渡されてきても,うまく動く関数を作ろう.
n=100〜1000程度で動作チェックすること.
void square_wave(double x[], int n); void sin_waves(double x[], int n, double f1, double f2, double f3);#include <math.h>
const double pi = 2.0*asin(1.0); // 円周率はこのように定義すると良い.asin = arcsin
void sin_waves(double x[], int n, double f1, double f2, double f3)
{
int i;
for(i=0; i<n; i++) {
x[i] = ( 1.0 * sin( 2*pi*i/n * f1 )
+ 2.15 * cos( 2*pi*i/n * f2 )
+ 3.00 * sin( 2*pi*i/n * f3 ) );
}
}
ここで,$\sin, \cos$ 関数の振幅の 2.0, 0.5, 0.25 は,説明用に適当な値を設定したので,各自で変更すること.
可能であれば位相も変化させてみよ.
注意:他の学生と異なる周波数・振幅・位相を設定すること.
| 例1:square_wave関数,矩形波 | 例2:sin_waves関数,正弦波の和 |
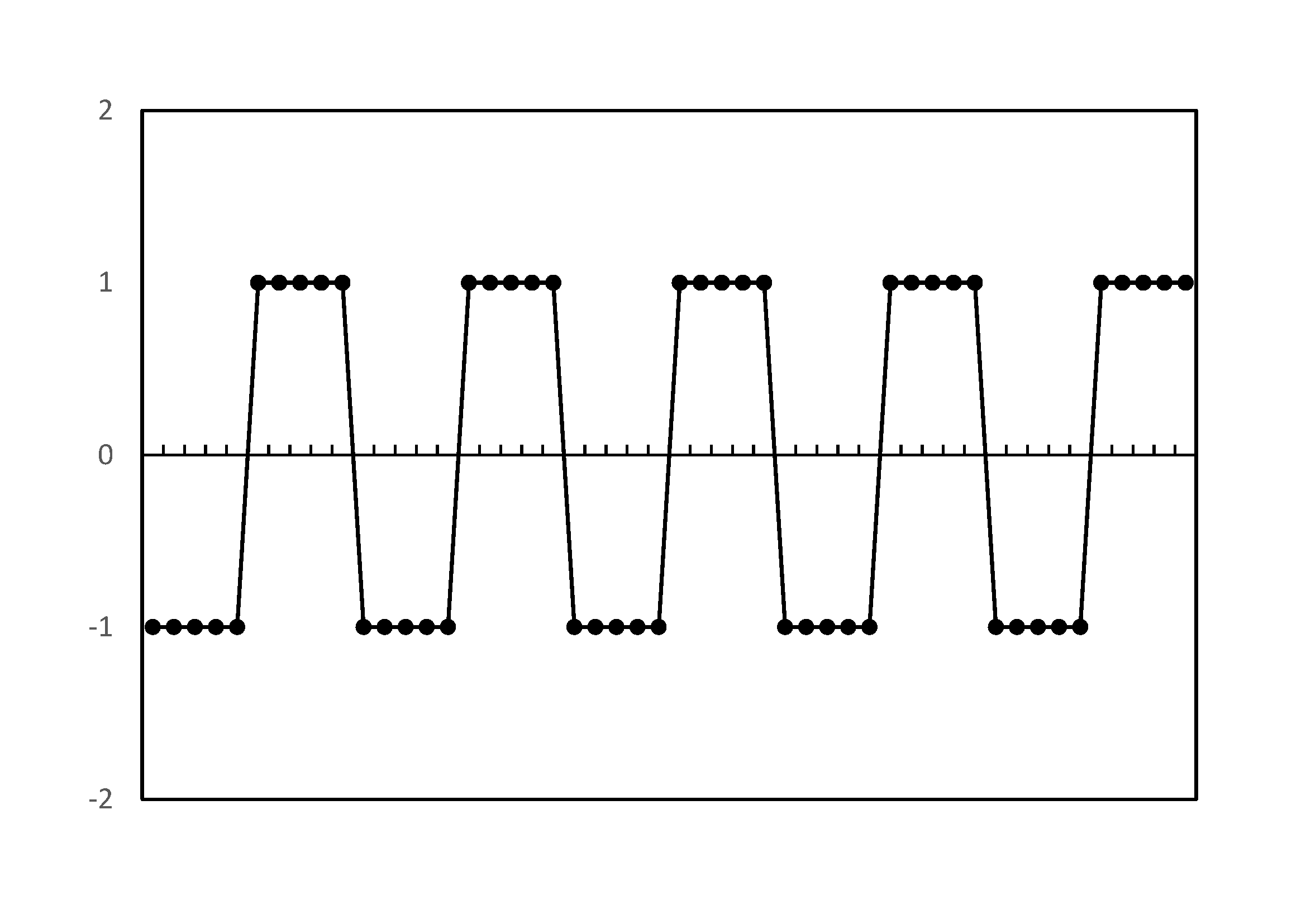 n=50, 周波数 5 の矩形波の例 |
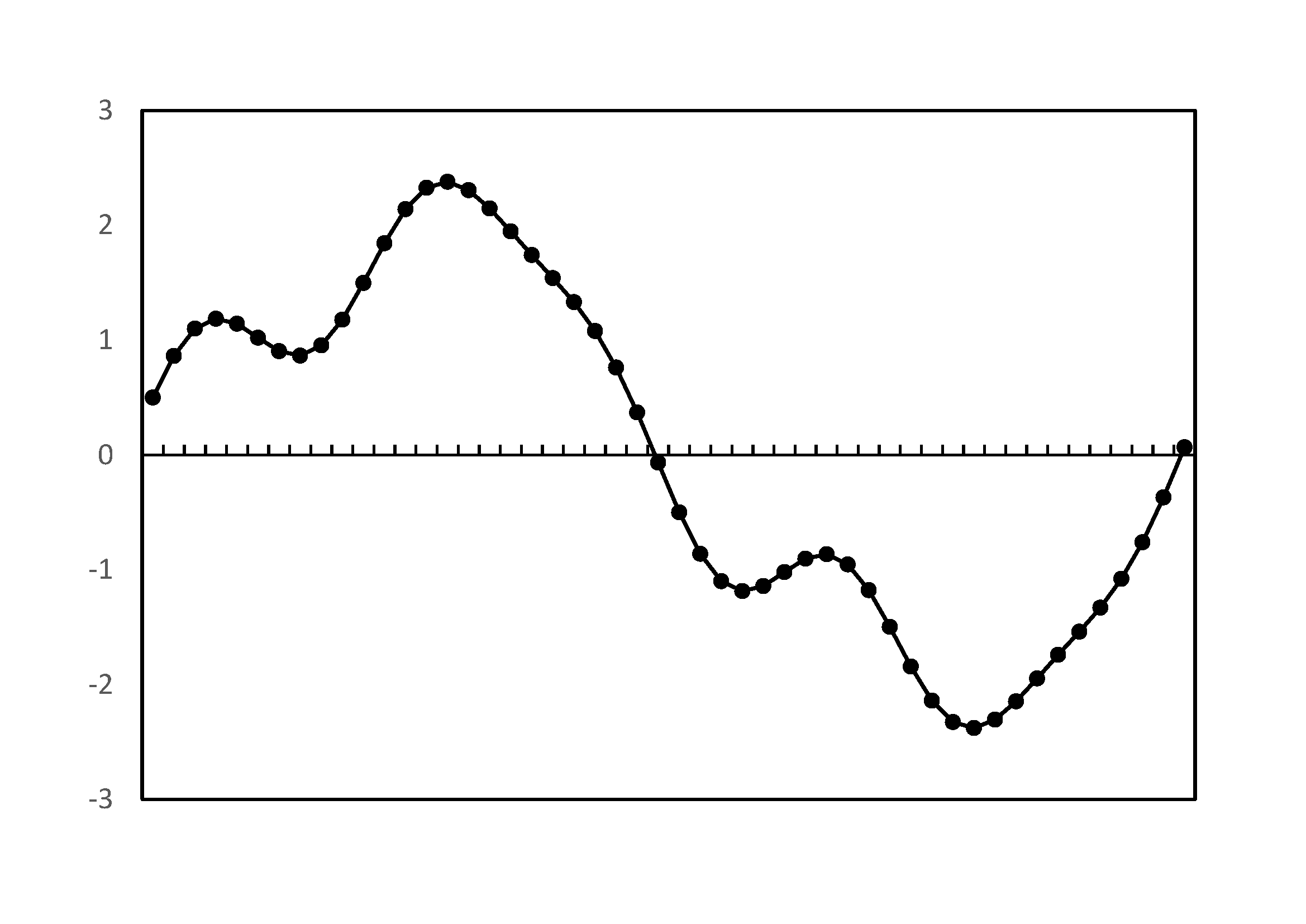 正弦波,余弦波の和の例 |
課題1で生成した波形データにたいして,本ページ内の離散フーリエ変換の式(\ref{eqn:dft}) を用いて,
f=0, 1, 2, 3, ... の場合における F の値を計算してみよ.
実数である元波形と,複素数である関数の内積であるので,結果は複素数となり,これがフーリエ変換後の関数の値1つ分に相当する.
ファイル名は153R000000-??-2.cpp とする.
実行例.値は正しいとは限らない. f=0 : F = 1.32123 + 2.3313 i f=1 : F = 0.32123 - 1.0301 i f=2 : F = -3.91284 + 0.3910 i ...
次週以降,これらの関数などを使うので,よくデバッグしておこう.