応用プログラミング演習(制御)(2)
今回は,実際の機器によく使われているPID制御(機械学会Web, Wikipedia)について実習を行う.
また,計算結果のASCIIグラフィクス表示に挑戦しよう.
PID制御
P制御では,偏差 $e$ ( = 入力SV - 応答PV ) に比例ゲイン $K_p$ を掛けて操作量 MV を計算するが,最終的に偏差がゼロにならず,いつまでたっても設定値にならない問題があった.(=定常偏差またはオフセットと言う)
実際の制御機器では定常偏差があると使い物にならないので,比例動作(P)に加え,偏差の積分(I)を用いるPI制御により,偏差をゼロに近づけることができる.
また,急激な値の変化に対して素早く応答するために,微分(D)動作を組み合わせて利用するPD制御や,これら3つを組み合わせたPID制御が用いられている.
参考:P = proportional, D = Differential or Derivative, I = Integral
位置型のP制御では,操作量 MV を
\begin{align}
MV &= K_p e
\end{align}
と与えることを学んだが,PID制御ではこれに加えて,$e$の微分や積分
\begin{align}
MV = K_p\left( e+ \frac{1}{T_I} \int e\ dt + T_D \frac{de}{dt} \right) \label{eqn:PID}
\end{align}
の項を追加して,操作量MVを決定する.
式\eqref{eqn:PID} の右辺第1項が比例動作,第2項が積分動作,第3項が微分動作であり,係数 $K_p$ は比例ゲイン,$T_I$ は積分時間,$T_D$ は微分時間と呼ばれる.
離散系では,サンプリング間隔を $\Delta t$ として,
\begin{align}
MV_n &= K_p\left( e_n + \frac{1}{T_I} \sum_{k} e_k\ \Delta t + T_D \frac{e_n-e_{n-1}}{\Delta t} \right) \hspace{1em} (位置型)\\
\Delta MV_n
&= K_p \left( (e_n - e_{n-1}) + \frac{\Delta t}{T_I} e_n + T_D \frac{e_n-2e_{n-1}+e_{n-2}}{\Delta t} \right) \hspace{1em} (速度型)
\end{align}
と表すことができる.
PID制御では,偏差の積分値や微分値などを用いて,滑らか,かつ,速やかに目標値に向かって制御することができる.
また,P制御の問題点であった定常偏差も大幅に減らすことができる.
ただし,P制御が比例ゲイン $K_p$ のみ調整すればよいのに対し,PID制御では設定すべきパラメータが $K_p, T_I, T_D$ の3つとなり,これらを適切に決定する必要がある.
(パラメータ・チューニングまたは最適調整と呼ばれる.)
まとめ
- P 制御のみでは定常偏差が残ってしまうため,I 動作を入れた PI 制御ではオフセットを減ずることができ,安定した温度制御などに用いられる.
- 目標値への素早い到達が必要な場合は,D 動作を加える.例えば,ライントレースロボットのように目標値が頻繁に変化する場合には PD制御も用いられる.
- これらを組み合わせた PID制御では,適切なゲインなどの設定により,正しい目標値に素早く到達させることができる.
課題
グラフィックスの利用
Excel や gnuplot などの外部ソフトウエアを使用する方法を学んできたが,ここではさらに簡易的にコンソールへのグラフ出力(アスキーグラフ,アスキーアート)を使ったプログラミングを紹介する.
最終的な提出用グラフの作成はExcelやgnuplotなどを用い提出すること.
課題1
提出物:ソースファイル,及びグラフ(Excel, gnuplot等で作成)の入ったファイル
P制御とPID制御それぞれについて,速度型・位置型のアルゴリズム例を示す.
それぞれgithub からダウンロードして実行してみよう.
いずれも計算結果の数値,および,ターミナルに Ascii Art を表示する.
参考:ソースコード中の fprintf(stderr, ...); は,標準エラー出力 stderr に文字列を出力する.
この方法では,ファイル出力と同じ fprintf 関数を用いて(> によるリダイレクトなしで)ターミナルに文字を出力できる.
なお,stderr の箇所を stdout にすれば,printf() 関数と等価になる.
方針:P制御およびPID制御を用いて,
- 時定数 T = 2.0 s
- シミュレーション時間 SimT は 5~10秒
- 初期値は PV = 0.0
- 目標値は SV = 1.0
の条件で計算を行い,グラフ表示することでその違いを比較してみよう.
この際,比例ゲイン $K_p$,積分時間・微分時間 $T_I$, $T_D$ を調整して,最も良いと思われる応答(=なるべく短時間で目標値に到達)波形を得よう.
比較のヒント:PID制御の式において,$T_I$をとても大きな値に,$T_D$をゼロにすれば,P制御となる.
今回のプログラムでは,計算結果の数値とともに簡易グラフが表示されるので,何回か試行しながら適切なパラメータを決めよう.
グラフ形状をおおよそ確認したら,各種パラメータ,および出力された数値データを,Excel, gnuplotなどに読みこませて,比較のグラフを描く.
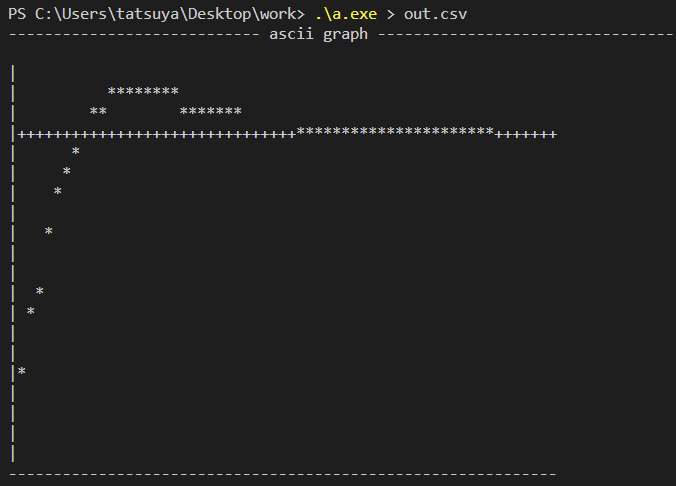 ターミナルに出力されるアスキーグラフの例.
ターミナルに出力されるアスキーグラフの例.
グラフはstderr に出力しているので,実行結果をファイルにリダイレクトしたとしても,画面に表示される.
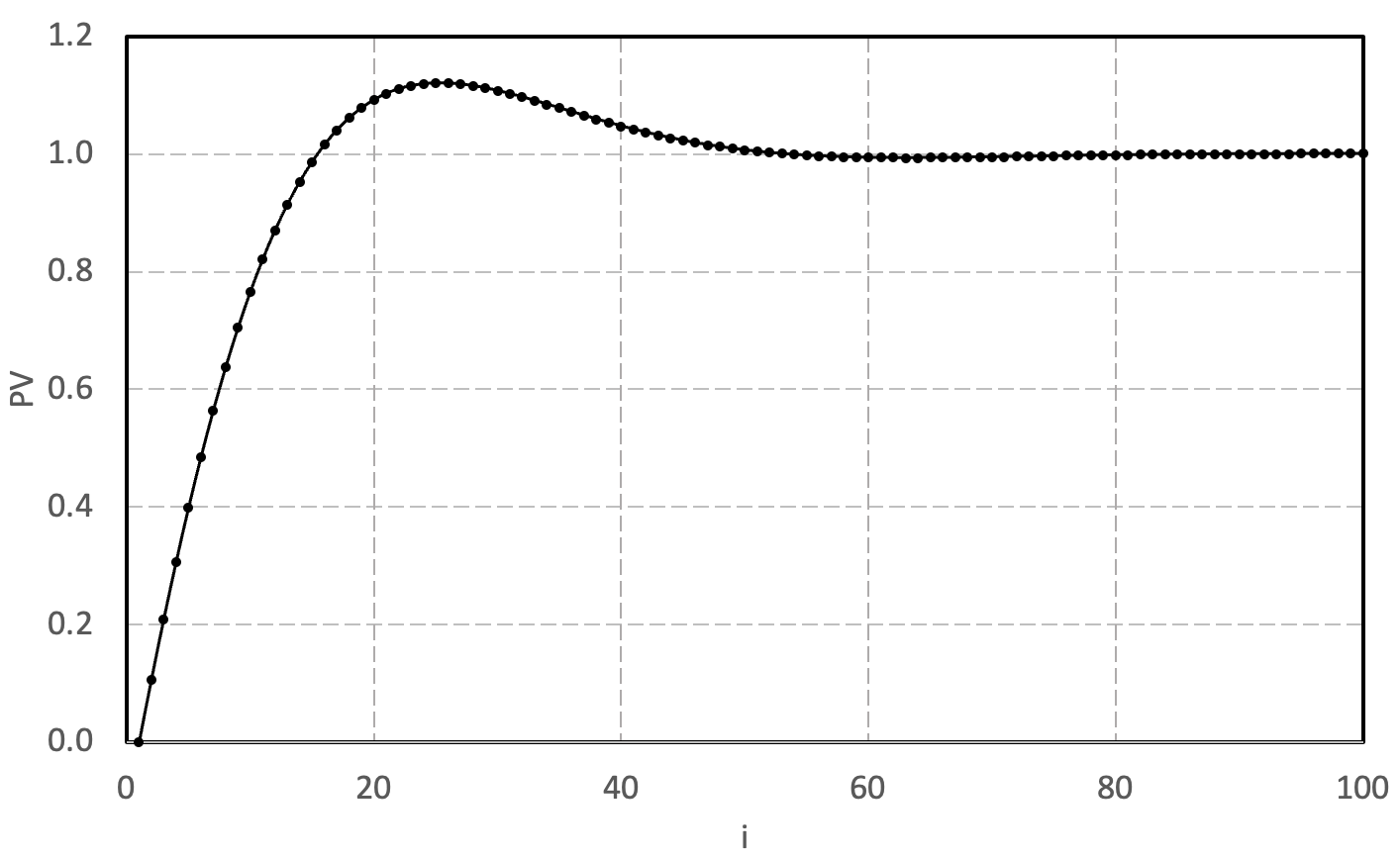 出力された数値データのグラフ表示例.P制御とは異なり,応答PVは目標値である SV = 1.0 に収束してゆく.
出力された数値データのグラフ表示例.P制御とは異なり,応答PVは目標値である SV = 1.0 に収束してゆく.
参考:gnuplotでcsvファイルを読み込んで,複数グラフ表示する方法
gnuplotでcsvファイルを読み込んで,複数グラフ表示する方法
out.csvファイルにデータを出力したとして,以下のコマンドでグラフが描ける.
gnuplot> cd 'D:\cprog20\myprog'
gnuplot> set datafile separator ','
gnuplot> plot 'out.csv'
さらに,グラフのウインドウを開いたまま replot コマンドで別のcsvファイル名を指定すると,同じグラフ内に複数の波形を重ねて描くことができる.
gnuplot> replot 'out2.csv'
ただし,ファイル名・フォルダ名に全角文字が使われている場合や,ファイルのエンコーディング(文字コード)の不一致でエラーが出る場合がある.
gnuplot> plot 'out.csv'
^
Bad data on line 1 of file out.csv
このような場合は csv ファイルをさくらエディタなどでいったん開き,文字コードを sjis や UTF-8に変更するとうまくいく場合がある.
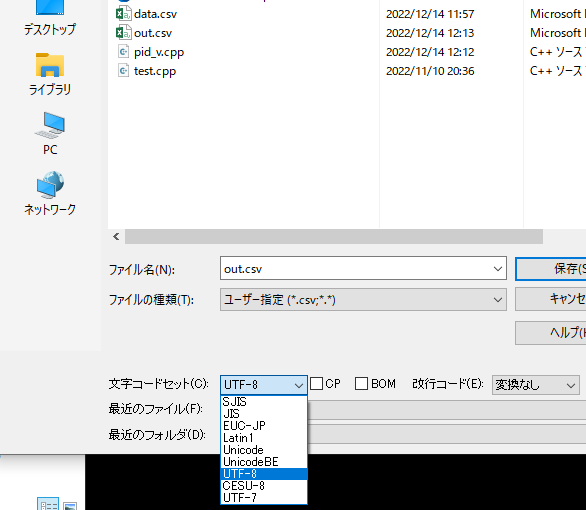 さくらエディタの例.データファイルを開き,「名前を付けて保存」でエンコードを変更し,同じファイル名で上書きする.
さくらエディタの例.データファイルを開き,「名前を付けて保存」でエンコードを変更し,同じファイル名で上書きする.
課題2
制御の数値シミュレーションを行うにあたって,シミュレーション結果をグラフなどの視覚表示することにどのようなメリットがあるか論ぜよ.
提出物:本課題について論じたWordファイルまたはTXTファイル (.docx, .txt形式)


