
今回はこれから学ぶで制御工学について,情報処理の観点から扱う.
制御工学で学ぶのは線形系であるため,基本は解析解(=紙と鉛筆で解けるもの)を求めることが可能な状態を扱う.
しかしながら,昨今の制御系はディジタル制御のセンサやデバイスを多用するため,
連続量でなくセンサなどから得られる「離散量を基にした制御」を考えておく必要がある.
私たちの身の周りには,空調の温度設定や,自動車の自動速度設定など, 機器などの動作状態を指示通りにコントロール(=制御)したい場合が多く存在する.
何かの対象の状態を計測し,それを元に所望の設定通りに状態を制御する方法の基本は,フィードバック制御と呼ばれる方法である.
動作原理は至ってシンプルで,
を行うことで実現できる.
以下に基本的な制御構造の原理図を示す.
図中の記号はそれぞれ,
である. これから頻繁に出てくる単語なので覚えておこう.
さて,操作に対して,制御対象が即座に反応して設定値に到達する (つまり,$SV == PV$) ならば制御の必要はないが,現実には操作と機器の反応には時間差が生ずる. これを遅れ,time-lagという.
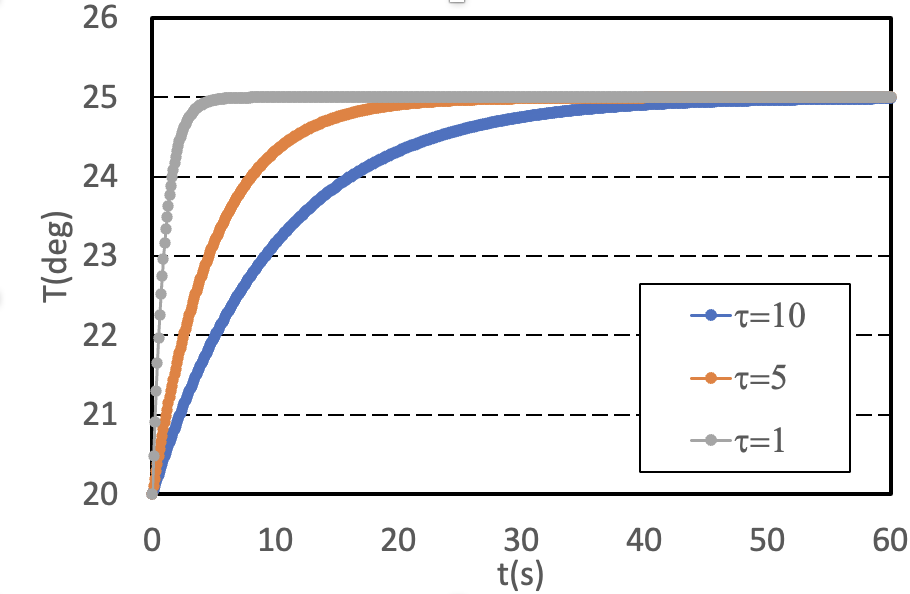
以下に一次遅れの例を図示する.
これはステップ応答とも呼ばれ,並進運動においては質量の大きな物体,モータなど回転運動においては慣性モーメントが大きなもの,伝熱現象では熱容量の大きなものほど,入力に対する応答の遅れが大きくなる.
一時遅れを式で示すと,
\begin{align}
T(t) = K\left(1-\exp(-\dfrac{t}{\tau}) \right)
\end{align}
となる.
ここで,$K$ は終端値となる定数である.
$\tau$ は時定数と呼ばれ,時定数は1次遅れの基本的な特性を示す.
(この式では,温度 $T$ と紛らわしいので,この説明に限り時定数=$\tau$と表記した.以降の説明では時定数=$T$としている)
$\tau$ は応答の遅れ具合と考えればよいく,この値が大きいほど,入力に対する反応の遅れが大きいことを意味する.
具体例として,エアコンなど空調機による室温制御では,室内の空気や壁面・床などの熱容量などに起因する遅れがある.
時定数が大きくなる要因として,部屋が広く気積が大きい場合,机など熱容量の大きなものが置かれている場合,壁に断熱材がなく剥き出しのコンクリートで囲われている,などである.
エアコンの制御では,暖房で設定温度(SV)まで温めようとする場合,温度(PV)の低い部屋にたいして,はじめは熱交換器の出力(MV)を高めにして暖気を室内に送り込むが,部屋の温度の測定値(PV)が,設定温度(SV)に近づいてきたら熱交換器の出力(MV)を下げて,徐々に設定値(SV)に近づける手順をおこなうことになる.
実際の機器の制御において,マイコンなどコンピュータを用いてデジタル制御を行う際には,操作量MVの計算を一定周期ごとに繰り返す処理が行われる.
この際,設定値 SV および計測値 PV から,具体的にMVをどのように決定するかが問題となる.
操作量 MV の決め方には様々なものがあるが,基本的には,目標値 SV と現在値 PV の離れ具合から操作量を決めると良さそうである.
まず,過去の操作量にかかわらず現在の操作量 MV を決めてしまう方式を「位置型制御」と呼ぶ.
これに対して,SVとPV から操作量 MV の「変化量」$\Delta MV$ を決めて,MV 更新する方式を「速度型制御」と呼ぶ.
速度型制御アルゴリズムでは,制御周期 $\Delta t$ を決め,その間に,計測,演算,操作量 MV の出力を繰り返して実行する.
以下の式で第 $n$ 回目の操作量を決定することが可能である.
\begin{align}
MV_n = MV_{n-1} + \Delta MV_n
\end{align}
この式は,前回の操作量 $MV_{n-1}$ に,今回の変化分 $\Delta MV_n$ だけ加える,という意味である.
制御の目的は,計測値 PV を目標値 SV に近づけることであるから,その差(偏差と呼び,$e = SV - PV$と表す)をいかに素早く減らし,最終的に $e=0$ にするかが重要となる.
言い換えれば,計測された偏差たいして,制御器を調整することで,システム全体の応答を様々に変化させることが可能である.
例えば,エアコンの場合は,設定温度(SV)と,現在の室温(PV)の差から,熱交換器の出力(MV)を決めてやればよいと考えられる.
一番単純な制御は,偏差の正・負で,制御器をON/OFFする「オン・オフ制御」である.
オン・オフ制御の例:
ON/OFF 制御は単純で安価に構築できるが,その性質上,値の変動が大きくなる傾向にあるので,その変動が問題とならないような場合に適している.
次にもう少し制御らしい方法を学ぼう.
いちばん基本的な制御は P 制御である.P は Proportional の略であり,「比例制御」とも呼ばれる.
(このほかにも,PD制御,PID制御などがある.)
最も簡単なP制御は,偏差 $e$ に定数 $K_p$(比例ゲインと呼ばれる)を掛けて,操作量 MV を決定する方法である.
P制御では,操作量 $MV_n$ を以下の通り与える.
位置型制御では現在の値のみでMVを決定する.
速度型制御では時間履歴が必要なため,制御ステップを表す添字の$n$が使われている.
つまり,位置型では「偏差の値」に応じて操作量を決定し,速度型では,「偏差の変化量」に応じて,操作量の増減を決めることになる.
いずれも,現在値と目標値が大きく異なれば変化を大きくし,目標値に近くなれば操作量を減じて微修正をする,と理解することができる.
実際の物理現象では,何らかの入力に対して,応答は慣性や熱容量などの影響により少し遅れて反応する.
ここでは,この遅れをモデルを用いて表現して,制御のシミュレーションを行う.
以下のようにモデル化したものを用いる.
制御対象の一次遅れ系において, $T$ を時定数として,目標値と操作量は以下の関係にある.
\begin{align} \frac{d}{dt}PV + \frac{1}{T} PV = MV \end{align} デジタル制御では,制御周期 $\Delta t$ ごとに制御するため,$n$ 周期後の応答は以下の式で示される. \begin{align} PV_n = ( T/ (T+\Delta t)) PV_{n-1} + ( \Delta t/ ( T+\Delta t)) MV_n \label{eqn:responce} \end{align} P 制御をかける場合は,与えるべき操作量は \begin{align} MV_n = K_p e_n = K_p(SV - PV_{n-1}) \end{align} となる.
上記のような制御アルゴリズムをプログラムで扱う場合,以下のような変数を用意すれば制御できる.
を用意すればよい.
添字の $n$ や $n-1$ は各時刻を表すが,各時刻の $PV$, $MV$ 値は全周期分保存する必要はない.
つまり,「現」制御周期と「前」制御周期に関するデータ2時刻分だけをメモリ上に保存しておけばよい.
また,制御の経過を逐次記録してグラフ化する場合は,各計算ステップごとに fprintf() などを用いてファイルに書き出しておくとよい.
提出物:(1)課題1で作成した関数と,それを使用した課題2のシミュレーションのソースファイル(1つにまとめる), (2)シミュレーション結果のグラフを記したファイル(.xlsx, .jpeg, .pngなど),の計2つとする.
上記のアルゴリズムを基に,位置型制御の関数を作成して,制御シミュレーションを行う.
以下の手順でプログラムを作成してみよう.
参考ソースファイル:githubのリポジトリ 上の ctrl_sample.cpp
注:参考ソースファイルは理解を促すためのものであり,丸写しでの提出は厳禁.
上記で作成した関数を用いて制御シミュレーションを行い,Excelでグラフを作成せよ.
シミュレーション(終了)時間は時定数の数倍(2〜3倍以上程度)とし,目標値を $SV$ = 25.0とする.(エアコンの室温など)
制御周期 $\Delta t$ は2-3種類,$K_p$ も2-3種類変え,比較のグラフを作成すること.
どのような相違が生ずるか考察せよ.
(すべてのグラフを重ねると見づらいので, $\Delta t$ ごとに,$K_p$ 違いの $PV$ 値を1つのグラフ内に描くと良い.)
なるべく短時間で目標値に到達するのが,制御の目標であるので,$K_p$を調整してグラフの変化を比較しよう.
処理の流れ
により計算できる.
初期値$PV_0$は 0 とし,前回の応答値$PV_{n-1}$ は $PV_n$ と別の変数を準備してループ内の計算が終わったら次のループのために現在値を代入すればよい.
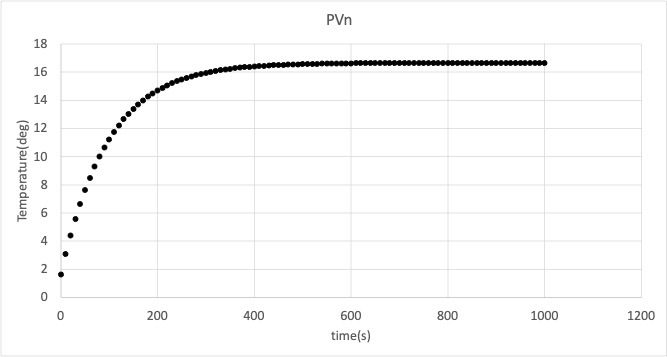
比例ゲイン$K_p$ = 2,制御周期 $\Delta t$ = 10 sec,時定数 $T$ = 300 sec,目標値 $SV$ = 25.0 で,計算終了時刻 $T_e$ = 1000 secまで計算したもの.
$K_p$ を0.5, 20, 50 など,大幅に変えて比較するとわかりやすい.
注:比例制御だけでは,最終的な偏差(オフセット)が 0 にならず,応答を目標値に一致させることができない. これを定常偏差と言う.