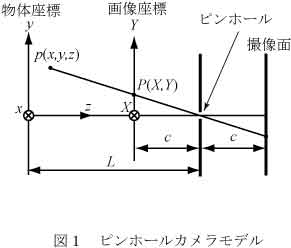
光学的モデルに基づいた投影関数として、ピンホールカメラモデルが挙げられる。ピンホールカメラモデルでは、測定対象から発せられた光が1点(ピンホール)を通って直進し撮像面に投影される。慣例に従ってピンホールに対して撮像面と対称な面を画像座標(X,Y)とすれば、(X,Y)は投影関数FX,FYにより次のように表される。
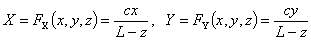
ここで、物体座標系(x,y,z)と画像座標系(X,Y)の相対的な位置関係およびcとLは図1に示す通りである。
PIVなどのように計測領域がx-y面に限定される場合にはz=0となり、次式で表される。
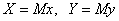 、但し
、但し 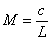
Mは像倍率に等しいので、x-y面に定規などを置いて撮影し、その画像から定規の像長さを求めることで算出される。
物体座標系に対して画像座標系が傾いている場合には、次の回転を考慮したピンホールカメラモデルが用いられる。
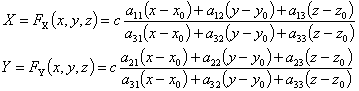
ここで、(x0,y0,z0)は物体座標系におけるピンホールの位置、a 11〜a 33は物体座標系を回転させるための回転マトリックスである。これらの係数は基準点データを基に最小二乗法によって決定される。ここで、基準点データとは物体座標とそれに対応する画像座標の組であり、後述の校正装置を用いて得られる。ピンホールカメラモデルは像歪みの無い理想的なカメラをモデル化したものであるが、実際にはレンズに収差が存在するため撮像面に投影される像は歪みを含む。歪みを考慮したピンホールカメラモデルも多く提案されている1)。