step04 機械情報と定量化
吉田民人の4階層モデルでは最下層（1階）にあたる機械情報について考えよう。このレベルの情報は、ICT（情報通信技術）の中核をなす。最大の特徴は、記号だけで、それに本来結びついているべき意味を扱わないことである。意味の処理は2階にいる人間に丸投げされているのだ。だからこそサクサク処理できるといってもよい。
シャノンの情報通信理論
こうした意味を捨象した、記号の側面だけになった情報、特に通信される電気信号としての情報について、定量的な理論を打ち立てたのが、アメリカの電気工学者クロード・シャノン※1である。
シャノンの情報通信理論によって、はじめて情報を定量的に計れるようになった。ICTに疎い人でも、彼が発明した情報量の基本単位ビット(bit)くらいは知っている。
シャノンと、共同研究者のウィーバーは、機械情報を考えるにあたり、図4-1に示すコミュニケーション・モデルを採用した。いろいろな書き方があるが、これが最もシンプルなバージョンだろう。このモデルは、電信や電話、無線による通信を想定したもので、それらへの応用には極めて有用である。
一方、機械情報の枠を超えた、つまり2階以上の情報の研究、たとえば
- 意味や価値の計量
- 人間同士のコミュニケーション
- 社会における合意形成
1 シャノンは、ベル研究所（後のアメリカ電信電話会社：ATT）の研究者であったから、通信される電気信号に限って研究したのは、当然の職務である。だが、もし彼がいなかったら、現在のようなICT全盛の時代がくるのは、10年、20年と遅れたに違いない。
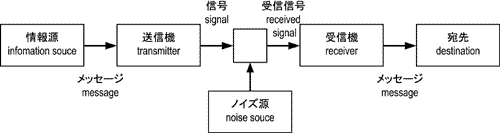
情報量の定義
図4-1のモデルを用いて、シャノンは情報源を「確率過程（事象系＝確率試行）」と考えることで、事象と事象系の情報量を定義した。
- 事象(event)の自己情報量
- 事象の起こる確率により定義される
- 事象系(event system)の平均情報量
- 起こりうる各事象の情報量の期待値により定義される。
対数
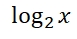とは、2を何乗したらxになるかというその何乗のことである。
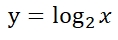のグラフを図4-2に示す。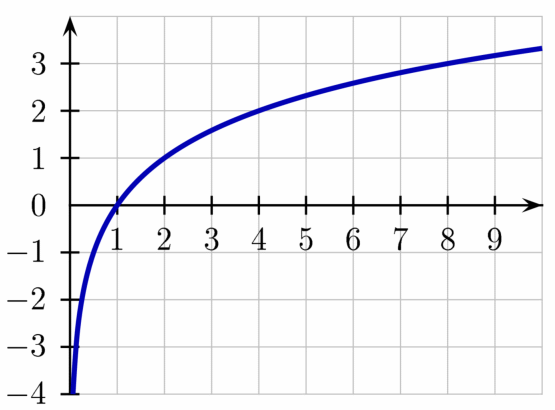
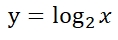のグラフ自己情報量
いま、事象aが確率pで生起するものとする。事象が生起したとき、これが与える情報量I(a)は、
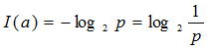
で定義される。
これは、その事象が起こったという情報を宛先受信したときに獲得する情報量と考えられる。この情報量を、事象の自己情報量(self information)という。ある事象の情報量は、生起する確率が小さいほど大きい。
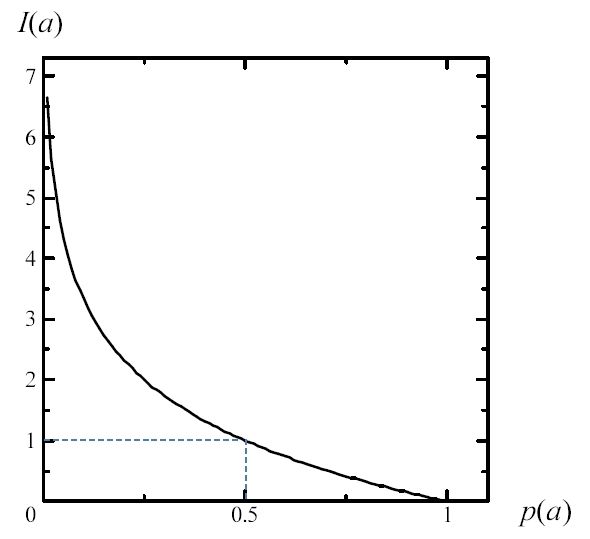
対数の底が2であるとき、情報量の単位はビット(bit)と呼ばれる。pは確率であるから、図4-1に示した対数グラフは、0～1の部分しか使わない。しかも負号が付いているから、あらためてI(a)のグラフを、図4-3に挙げておく。1bitが確率1/2に相当する情報量であることがわかる。
たとえば、サイコロで1の目が出たという事象の自己情報量は、
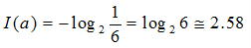bit
である。また、52枚のトランプから1枚引き、表を返して見たときにあなたが得る情報の自己情報量は、
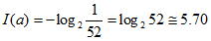bit
である。100万人に1人の栄冠に輝いたときの自己情報量は、
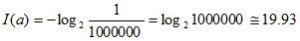bit
となる。100万人に1人の災難に遭遇しても同じだ。このように情報量は、事象の内容（つまり情報の意味）には関わりなく、まれな事象ほど大きくなる。犬が人を噛んでもニュースにならないが、人が犬を噛めばニュースになるということわざ(?)は、ニュースの価値が、読者や視聴者が得る情報量で決まることを暗示している。
平均情報量
個々の事象の自己情報量に基づいて、事象系の平均情報量が定義される。ここで事象と事象系の区別をハッキリしておこう。
- 事象系
- サイコロを振る。宝くじを買う。明日の天気……
- 事象
- 1の目が出た。2等が当たった。今日は雪だった……
a1, a2, ..., an
とする。排反とは、どれか1つは必ず起き、2つ以上は同時に起こらないことだ。明日の天気は分からなくても、なんらかの天気には必ずなるではないか。そこで、anが起きる確率をpnとすれば、
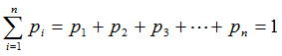
になる。
さて、この確率試行を行って、事象aiが起こったときの自己情報量I(ai)は、定義により、
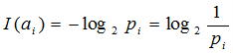
であった。
ここで、すべての場合について、自己情報量とそれが起きる確率piの積を合計すれば、その確率試行で得られるであろう情報量の期待値が求められる。
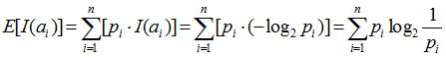
この量E[I(ai)]を、平均情報量(average information)という。自己情報量の期待値は、情報源から生ずるだろう情報量の平均とも考えられるからである。情報工学では、この量をエントロピー(entropy)と呼ぶ※2。
平均情報量は、どの事象が実際に起きたかとは関係なく、事前に決まる、事象系に固有な量である。一方、自己情報量は、実際に起きた事象によって、事後に決まる量である。
2 後述のように、《エントロピー》は、熱力学に端を発し、情報学、自然現象、はては社会現象から精神現象まで、さまざまな領域で使われる。やや乱発気味ともいえるが、すべての領域での最大公約数てきな意味は、秩序－混沌の尺度または乱雑さの程度であろう。
たとえば、サイコロを振るという確率試行の平均情報量は、1から6までの目が出た自己情報量の平均だから、
るから、やはり、
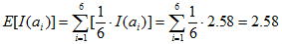bit
である。面白くも痒くもない。サイコロのように、どの場合の確率も同じ確率試行では、平均情報量＝自己情報量となる。等しくないのはイカサマのサイコロだ。
もう少し面白みのあるテーマとして、宝くじを考える。
起こりうる事象の中に、非常にまれなもの（1等10億円！）が含まれていると、平均情報量が跳ね上がると思うかもしれないが、前述のように、平均情報量は各自己情報量の、発生確率で重み付けした平均なので、そうはならない。各等の当選確率は異なるので、平均情報量は表4-1のように計算される。
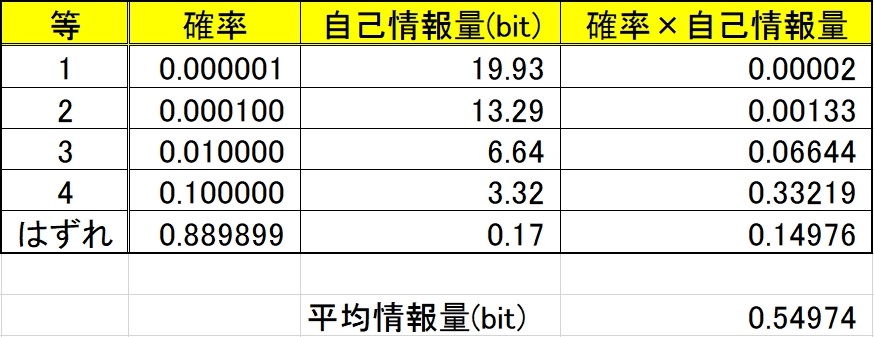
自己情報量と平均情報量は、通信路の容量や、信号と雑音の関係を論ずる基礎になっている。また、コンピュータで処理されるデジタル情報についても、この情報量の定義(bit)が使われる。
演習：データのディジタル化と情報量
デジタル化された（2進数で表現された）データについて、情報量の計算方法を知ろう。
- 色
- フルカラーと呼ばれる、RGB各色256階調で表現された色は、何Bのデータだろうか？
- 文字
-
- 英数字（半角文字）は、1文字につき1が1B
- かな漢字（全角文字）は、1文字につき2B
- 画像（静止画）
- フルハイビジョン（横1920ドット×縦1080ドット）の静止画像は、何Bのデータだろうか？ 4K（横3840ドット×縦2160ドット）ではどうか？
ヒント：画素(pixel)の数を計算し、それに色のデータ量をかければよい。 - 音声
- CD1枚に格納できるデータの容量は何バイトだろうか？
ただし、CD1枚には、1秒間に44100回のサンプリング、信号レベルは16ビットで74分までのステレオ音声（左右2チャンネル）が格納できる。
- 動画
- フルハイビジョン画像が1秒間に30フレーム（30fps）で表示される動画データは、1時間につき何バイトか？
- MP3 音声向け
- JPEG 画像向け
- MPEG 動画向け
データをデジタル化する最大の利点は、色、文字、画像、音声、動画など、表現メディアの種類によらず、すべて2進数という数に変換されるので、貯蔵・伝達・処理などすべての情報処理で同じ技術（コンピュータ）が使えることにある。それぞれのアナログな記録手段（本、レコード、フィルムなど）を思い出してみれば明らかだろう。
デジタル量とアナログ量
機械情報のすべてが、デジタル量ではない。アナログ量を扱う機械も存在する。
むしろ本来の情報はアナログ量であることが多い。デジタル量とアナログ量は、つぎのように定義される。
- デジタル量
- 離散量。とびとびの値をとる量のこと。バス料金、人数、文字や文章、デジタル時計の時刻など
- アナログ量
- 連続量。連続的に変化する量のこと。色、画像、音声、温度、アナログ時計の時刻など
たとえば、（アナログな）温度計の目盛りを読むことは、A/D変換の一種である。26℃とか26.1℃などと目盛りを読む時には、小数点以下を切り捨てるか、四捨五入する操作がはさまっているのだ。すなわち近似である。近似には誤差が伴う。この誤差を量子化誤差(Quantization Noise)、変換後のデジタルデータの情報量が大きいほど小さくなる。
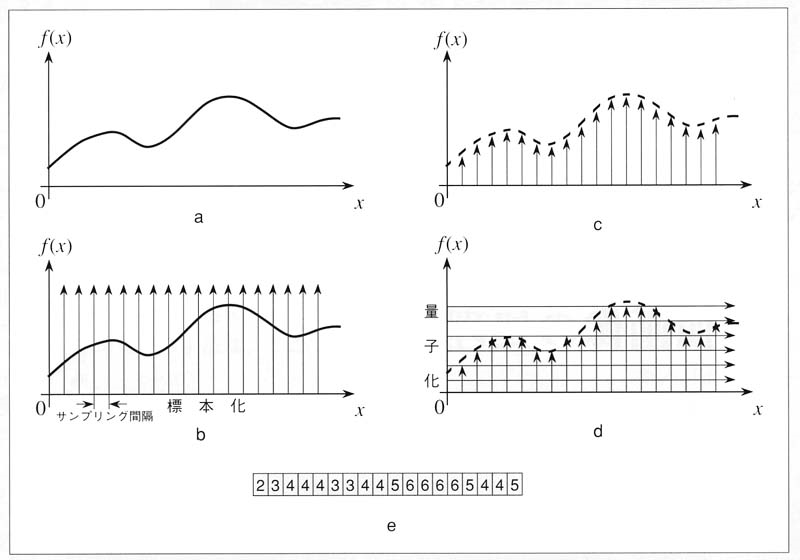
シャノンの標本化定理
A/D変換（デジタル化）に関する基本定理である。時間的に変化するアナログ信号（音声など）をデジタル量に変換するには、
- 一定のサンプリング間隔で信号レベルを測り（標本化）
- 信号レベルの目盛りを読んでデジタル量で表す（量子化）
このとき、元のアナログ信号を忠実に再現するためのサンプリング間隔を決めてくれる定理が、以下に示すシャノンの標本化定理である。
アナログ信号に含まれる最高周波数成分の2倍の周波数（fs:サンプリング周波数）で標本化すれば、元の信号波形を完全に表せる。
また、音楽CDのサンプリング周波数は、前項の演習で見たとおり44,100Hzであるから、その1/2の22,050Hzまでの音声信号を表現できる※3。
この標本化定理は、サンプリング間隔のみについての理論で、量子化（目盛りを読む）に伴う誤差とは関係ないことに注意が必要だ。超高速で大ざっぱに目盛りを読んだら、やはり大ざっぱにしか復元できない。量子化誤差を少なくするには、標本化1回あたりのデータ量（量子化ビット数）を多くすればよい。現在ではCDの16bitに対し、24/32bitなどを用いたハイレゾオーディオが普及しはじめている。
3 オーケストラの一番高音が出せる楽器の一番高い音というのは都市伝説で、実際は当時のVTRを流用するという技術的理由によるものである。ちなみに、74分という最長収録時間は、ベートーヴェン：交響曲第9番、カラヤン指揮／ベルリン・フィルという音源の長さから取られたと信じているのだが、これも都市伝説なのだろうか。
エントロピー
機械情報と高次の情報を橋渡しする概念
《情報量》と密接に関係するのが、《エントロピー》である。情報工学では平均情報量をこの名前で呼んだことを思い起こしてほしい（前述の※2）。
この概念は熱力学から生まれた。熱機関の研究をしていたドイツの物理学者、ルドルフ・クラウジウスが提唱者である。しかし現在では、情報学、自然現象や社会現象、はては精神現象まで、さまざまな分野で広く使われる。
エントロピーの定義は、学問領域ごとにかなり異なる。ここでは、それらの定義を概観し、エントロピーをめぐるさまざまな言説に接することで、その大体の概念を理解し、それが私たちの《生命》や広義の《情報》とどう関わるのか考える。
熱力学におけるエントロピー
熱力学は物理学の1分野で、熱や物質の輸送現象およびそれに伴う力学的仕事について、系のマクロな性質から研究する学問である。マクロな性質とは、たとえば気体系については体積・圧力・温度などのことだ。つまり熱力学は、気体の分子状態といったミクロな性質には踏み込まない。前述の※2で、各分野の最大公約数的な《エントロピー》の定義は、乱雑さの程度だと述べたが、実は純粋な熱力学上のエントロピーには、困ったことにこの定義が当てはまらない。クラウジウスも、原子や分子の実在を仮定していなかった。彼の定義によるエントロピーSは、
dS = dQ/T
クラウジウスが気づいたのは、理想化された仮想熱機関であるカルノーサイクルでは、dSの、熱機関の1サイクルに沿った変化の積分量は0（つまり可逆）になるが、現実の熱機関では負（不可逆）になることであった。これは後に、熱力学第2法則として定式化された（熱力学第1法則はエネルギー保存則のことだった）。
熱力学第2法則：
エネルギーの出入りのない系（断熱系＝閉じた系）では、エントロピーは常に増大する。
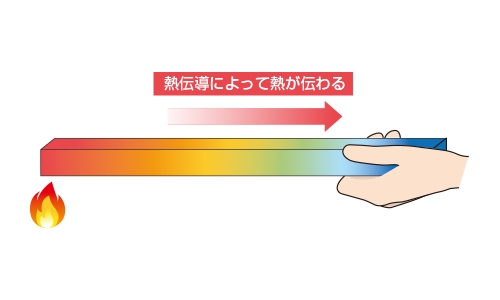
手に持った金属棒を炎にかざし、熱がどのように伝わるかを見る。なにやら愚かな行為に見えるが、この図の時点で火から外したら手は無事だろうか？ エネルギーの流入が止まることで、金属棒は閉じた系になるので、これ以上の変化はないだろうか。
そんなことはない、ということはご存じの通りだ。手元に熱が伝わってきて、アッチッチと棒を取り落とすのは目に見えている。
別の実験（図4-6参照）を考える。
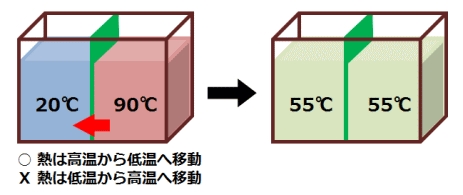
もう1つだけ実験しよう（図4-7参照）。
熱の本体と統計力学
熱力学第2法則は私たちの直感と合致している。または、われわれが住む世界の時間の矢の方向を熱力学第2法則が決めているということもできる。つまり、私たちは、エントロピーが増大する方向を未来としている。
この法則は熱伝導やインクの拡散だけでなく、私たちの世界のさまざまなところに表れる。たとえば図4-8にある部屋の入居直後と3年後の様子を示す（私や家族の部屋ではない）。
実は、私たち生物の体を構成する1つ1つの細胞も、この部屋のようなものである。人間は60兆個とか、最近のより緻密な推定では37兆個とかの細胞から構成されているが、細胞にも時間とともに老廃物が貯まり、逆に必要な物質が不足する。細胞は自分の内部を掃除するために、新陳代謝という驚くべき精緻な仕組みを進化させてきた。細胞のエントロピーを下げながら生き続ける、これが自己保存の働きである。そのために生物が、さまざまな記号を駆使した情報処理を行っていることは、step03で学んだ通りである。《エントロピー》が、機械情報と人間や生命をつなぐ重要な概念であることが、少しは伝わったであろうか。
ここから先はやや難しいので、お話として聞いてほしい。
ところで、熱力学第2法則といっても、実は、古典力学としての熱力学だけでは、熱が高温から低温にしか流れない理由は説明できない。乱雑さというような概念がエントロピーに関わってくる余地もない。なぜなら、古典熱力学はたとえば気体系について、マクロ状態しか扱わないため、導き出される物理現象は、どれも時間に対して可逆的になり、時間の矢を導き出せない。それには、どうしても物体（固体・液体・気体）の分子・原子についてのミクロな物理法則を使って、マクロな性質（エントロピーの増大）を導き出すしかない。その過程で、熱の実体も明らかになるはずである。
結論から言えば、熱の実体は、物質を構成している分子の運動エネルギーである※4。それを総和としての熱エネルギーではなく、ミクロに扱うとは、個々の分子が取り得る物理的状態とその確率について、統計的に計算することである。エントロピーが増大する、つまり時間とともに乱雑さが増していく理由は、その確率の方がはるかに大きいからと言う以外に、ありえないではないか。
4 固体では分子の振動エネルギー、気体では自由運動のエネルギーという違いはあるが、分子運動が熱の実体である点は同じ。液体についての熱モデルはやや複雑である。
この困難なテーマに挑戦し、統計力学を打ち立てたのが、オーストリアの物理学者ルードヴィッヒ・ボルツマンである。結論として、彼は系のエントロピーSの別の定義を導き出した。
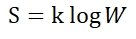
Sはエントロピー、kはボルツマン定数、Wは与えられたマクロ状態に相当するミクロ状態の数である。ここにおいて初めて、系の乱雑さという統計的・確率的概念が、エントロピーと結びついたのである。統計力学は、古典熱力学から量子力学に橋を架けたといわれる物理学の金字塔である。
エントロピーをめぐる言説
熱力学
1. 熱力学のエントロピーとは、ある種の無秩序さ(disorder)を表す量である。すなわちある瞬間において、その系がいかなる微視的状態にあるかということに関する、不確定さを表している。（瀧保夫『情報論I』）
情報学
2. 情報のエントロピーは、通報を受けとる以前における、通報の状態に関する知識の不確定さを表しているといえよう。実際に通報を受け情報を得ることによって、この不確定さが取り除かれるのである。一言にしていえば、平均情報量とはそれによって取り除かれる不確定さであるということができよう。（瀧保夫『情報論I』）
自然現象
3. エントロピーという量を導入し、この名前をつけたクラウジウスは、熱力学を全宇宙※5に適用すれば、
- 全宇宙のエネルギーは一定であり、
- 宇宙のエントロピーは増大し、ある最大値へ近づくであろう、
4. 秩序を維持し、さらに（生長などで）それを拡大するためには、生物体は絶えずエントロピーを外に排出し、負のエントロピー（ネゲントロピー）を取り入れねばならない。シュレーディンガーの言い方を使えば、「生物体は負のエントロピーを食べて生きている」ということになる。（小出昭一郎『エントロピー』）
5. しばしば、生物活動やその延長としての人類による経済活動は地球上のエントロピー増大過程であり、資源枯渇や環境破壊はその結果であるといわれる（安孫子誠也「エントロピー」『コンサイス20世紀思想事典』）
5 全宇宙は最大の閉じた系である。なにしろ外がないのであるから。いつかは、それ以上変化しない熱死状態を迎えることになる。
社会現象
6. ナショナリズムや、ナショナリスティックな運動は、とかく、エントロピー的になりやすい。すなわち、ナショナルな秩序を守ると称して世界的な秩序を破壊しやすいものである（ケネス・ボールディング『二十世紀の意味』）
精神現象
7. ギリシア語のアガペという意味の愛は、あらゆる人間関係のうち最も反エントロピー的なものである（ケネス・ボールディング『二十世紀の意味』）
8. 愛とは反エントロピー的なものではない。仮に愛が反エントロピー的なものであるならば、愛は生成とは相反する力ということになろう。というのは、エントロピーの流れと生成とは同一の歩調を取るものだからだ。愛とは、むしろ展開過程に対する崇高な約束行為である」（ジェレミー・リフキン『エントロピーの法則』）