コンピュータ機械工学

第11回バイナリデータ・ビット演算・データ計測

11.1 バイナリとは?

ここに述べることは、C言語に特有の話ではなく、現在の2進数をベースにしたコンピュータの性質そのものに起因する事柄である。バイナリ(=binary)とは、「2進数の」という意味である。例えば以下のように、8ビット(=1バイト)のデータが一つあったとしよう。

char a;   (符号付き変数であることに注意)

このデータはメモリ上では1バイト分のメモリを消費する。これにある値を代入すると、

a = 64;

これを2進数で表せば、

0 1 0 0 0 0 0 0

となる。コンピュータの中のメモリは、一つの場所(=セル)あたり、1ビットしか記憶出来ないので、2進数の状態で格納されているのである。

a = 127; <---> 0 1 1 1 1 1 1 1
a = -1;  <---> 1 1 1 1 1 1 1 1

しかし我々が普段見慣れているのは10進数による表現であるので、ふつうは10進数に変換して目に見える状態にしている。つまり、a = 64ならば、64すなわち'6' と '4'という2つの「文字」に変換する。この文字はASCIIキャラクタといい、ASCIIキャラクタコード表に則して変換される。printf文やscanf文はこの変換を自動的に行っている。

printf("%d",a); ----> 64 (6と4という文字がプリントされる)

同様に、文字列についてもコンピュータの内部では2進数の状態で取り扱われることになる。

例題

ASCIIキャラクタコード表を参考に、各自の名字のアルファベットについて、キャラクタコード番号を画面に表示し、併せて小文字を大文字に変換して表示するプログラムを作成せよ。
```
実行例：compmech ->
	c = 63	c -> C
	o = 6F	o -> O
	m = 6D	m -> M
	p = 70	p -> P
	m = 4D	m -> M
	e = 65	e -> E
	c = 63	c -> C
	h = 68	h -> H
```

16進数表現

2進数の表現はやたらと桁数が増えるので、4ビットごとにまとめて0,1,2,...8,9,A,B,C,D,E,Fの16進数で表すことが多い。
C言語で16進数であることを示すには、0x1234など数字の頭に"0x"をつける。

11.2 整数の表現(特に、負の整数)

バイナリデータを取り扱う際には、まず変数の型を意識する必要がある。以下はC言語で用いられるデータ型と、(32ビット処理系における)ビット幅である。

データ型とビット幅の一覧表

プラスの整数については、10進数と2進数の変換はそれほど難しくはない。マイナスの整数については、2進数でどのように表現されるかを注意する必要がある。
マイナスの数がコンピュータの内部でどのように表されているのかを把握するために、以下のプログラムを入力し、実行せよ。
なお、このプログラムの内部では、後で説明するビットシフト演算を用いている。

bin_disp.cpp

このプログラムは、10進数で数字を与えたときに、それに対応する16進数および2進数を表示するものである。例えば -123 という数字の16進数および2進数表現を表示させると、以下のようになる。
なお、サンプルプログラムでは、入力した数を格納し、結果の表示に用いる変数は、4バイト(4*8=32ビット)のint型で宣言されている。

Z:\compmech\ch11>bin_disp -123
Input integer number: -123

Hexadecimal: ffffff85
Decimal: -123
Binary: 11111111111111111111111110000101

マイナスの数については、上位ビットにずらっと1がならぶ(16進数表現ではfが並ぶ)ことが確認できる。
なお、int型のビット幅は 32bit である(正確には処理系依存)。
特に、プラスの数については最上位のビットが0となり、マイナスの数については最上位のビットが1となることから、 signed型の値については最上位のビットを符号ビットと呼ぶことがある。

注意

例えば符号付きchar型では、-1 は、10000001 ではなく、11111111 である。1 + (-1) = 0 という演算をやってみると理解できる。符号ビットは符号そのものではないことに注意すること。
キーワード： 2の補数で検索してみよう。
データ型については、前回のWebをチェックしておくこと。

皆がこれまで利用してきた int型や char型は、全てsigned型であり、マイナスの数を表わすことができる型であった。
一方、定義する変数がプラスの値しかとらないことがあらかじめ判っているのであれば、unsigned型を利用した方がプログラム上の誤りが少なくなるし、また、より大きい値を取り扱えるようになる。
厄介なのは、singed 型と unsigned 型で、「内部表現」が同じ場合でも、異なる数字を意味することがあることである。
なお、以下は1バイト整数である char型を用いて説明を行うことにする。

例えば、0xD0(2進数表現では11010000)は、unsigned型では 208、singed 型では -48 となる。

0xD0
unsigned型：208
singed 型：-48

11.3 ビット演算

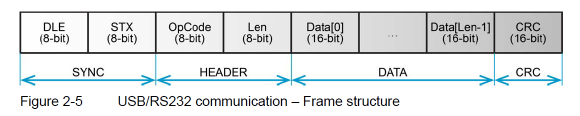
11.4 に述べるAD変換や、コンピュータ間の通信(Ethernet, CAN, シリアル通信, etc.)の際に、ビットをダイレクトに操作することがある。例として、モータを制御する際に、PCからモータのコントローラに対してシリアル通信で送信するデータの構造を以下に示す。(Maxon社のマニュアルより引用)

このデータ構造に対応して、以下のようなデータを通信することによりモータを制御することができる(なお、この値は適当である)。このようなデータを送受信するプログラムを書く際には、ビット演算が必要となる。

90 02 3A C4 00 00 28 BF D4 16 ...

&演算子 (AND演算子)

&演算子は、ビット毎の積を計算する演算子であり、演算結果は以下の様になる。

a	1	0	1
b	0	1	1
a & b	0	0	1

この表より、

0で&演算を行えば(=マスクすれば)演算結果は必ず0になり(これを0クリアと呼ぶ)、
1で&演算を行えば、他方の値をそのまま取り出せる。

ことがわかる。

| 演算子 (OR演算子)

| 演算子は、ANDとは反対にビットを強制的に1にするために用いられる。

a	1	0	1
b	0	1	1
a \| b	1	1	1

~演算子 (NOT演算子)

~は、ビットを反転させる演算子である。~0は1であり、~1は0である。

ビットシフト演算～左シフト

例えば以下の様なデータ(0x1A = 26)があったとき、

これを左に2ビットシフトすると

になる (0x68 = 104)。これは元のデータを4倍(=2の2乗)したことと意味は同じである(ただし演算速度は何十倍も異なる。最近の高機能なコンパイラの中には一般の乗算をシフト演算に置き換えるものもある)。
C言語においてこの演算は

int a = 26;
a = a << 2;
// a <<= 2; としても同じ

などと書く。

ビットシフト演算～右シフト

左シフトと異なり、右シフトは符号付きと符号なしの場合で演算結果が異なるので注意が必要である。符号なしの場合、

シフト前(0xD0 = 208)	1	1	0	1	0	0	0	0
2ビットシフト後(0x34 = 52)	0	0	1	1	0	1	0	0

シフト前(0x50 = 80)	0	1	0	1	0	0	0	0
2ビットシフト後(0x14 = 20)	0	0	0	1	0	1	0	0

の様になる、一方、符号ありの場合、

シフト前(0xD0 = -48)	1	1	0	1	0	0	0	0
2ビットシフト後(0xF4 =-12)	1	1	1	1	0	1	0	0

シフト前(0x50 = 80)	0	1	0	1	0	0	0	0
2ビットシフト後(0x14 = 20)	0	0	0	1	0	1	0	0

の様になる。これは、負の数がどのようにビット表現されるかを考えれば理解出来る。

11.4 AD変換

変位・速度・力・電圧といった物理量を把握する際には、センサが用いられる。計測する物理量に応じてセンサにはさまざまな種類のものがあり、またセンサが出す信号にもさまざまな種類があるが、代表的なものとしては、物理量に対応した電圧値を信号として用いるものが挙げられる。

例：機械工学実験２実験B 減衰自由振動で用いた変位センサや加速度センサ
一方、ロータリエンコーダのようにパルスの数で物理量を表したり、電流値で物理量を表すセンサなどもある。

センサによって計測される物理量の値と電圧との関係は、センサの検定表(校正表)などに明記されている。この関係を用いることにより、電圧値から物理量を算出することが出来る。
センサが出す信号は、基本的にはアナログ量であることが多い。このアナログ量をデジタルなコンピュータに取り込み、信号の情報をデジタル化することを「AD変換」(AD: Analog/Digital)という。また、より一般的な表現として、アナログ量をデジタル化することは「量子化」とも呼ばれる。

計測レンジ

センサが出力する電圧範囲は様々である。例えば、-10 V ～ +10 V の範囲で電圧を出力するものもあれば、+2 V ～ +3 V の範囲で出力するものもある。 AD変換を行う各種デバイス(計測ボード, マイコン, etc)では、0～5 V, 0～10 V, -5～5 V, -10～10 V などから計測レンジ(レンジ=範囲)を選択できるものが多い。なお、電圧値を正の範囲のみで計測するものをユニポーラ(単極性)、プラスマイナスの範囲で計測するものをバイポーラ(双極性)という。 AD変換を行う際には、後述する量子化精度の影響を最小限に抑えるため、計測対象となるセンサの出力範囲を把握し、AD変換を行う電圧のレンジ(範囲)を適切に選択する必要がある。

量子化精度(分解能)

AD変換を行う際には、量子化精度(分解能)に配慮する必要がある。量子化精度には、8ビット、10ビット、12ビット、16ビットなど様々な種類があり、デバイスによって異なる。ビット数が大きいほど、分解能が高いということになる。

バイナリデータ

アナログの電圧値がコンピュータ内部でどのような値に変換されるのかを把握するためには、計測レンジと量子化精度の両方を考慮する必要がある。例えば、分解能が8ビットの場合でも、計測レンジが 0～5 V と -5～5 V の場合で、AD変換後の値が以下のように異なってくる。

 0[V]～5[V]       <---> 0x00～0xFF (ユニポーラ型)
-5[V]～0[V]～5[V] <---> 0x80～0x00～0x7F (バイポーラ型, コンプリメントバイナリ)

アナログ電圧が10ビットデジタルデータに変換された場合を考える。この時点では、変換されたデジタルデータは実際の物理量を直接表しているわけではないので、適当な変換を行う必要がある。例えば、0～5 V の範囲のユニポーラでA/D変換をした結果が adc10u() という関数の返値で得られるとすると、電圧を求める処理は

unsigned short a = adc10u(); // a はA/D変換されたバイナリ値
    float x = (float)a*5.0/1024; // x は電圧値 aの値はまずfloat型にキャストしている

となる。(-5～5 Vのバイポーラの場合はどのようになるかは各自考えること)

11.5 課題 (提出期限: 金曜日22時)

data.txtには、12bitのA/Dコンバータにより、時間刻み幅1msで6秒間計測されたデータが2進数で記録されている。この値が
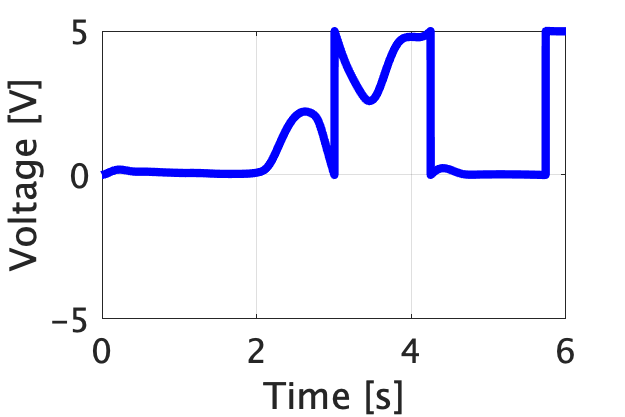
- 0 V ～ 5 V のユニポーラ型で読み取った電圧値
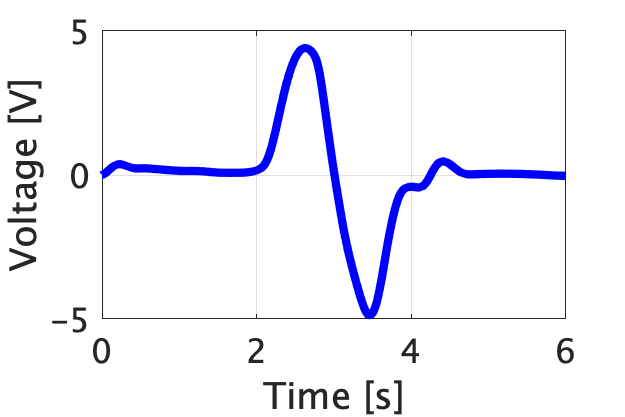
- -5 V ～ 5 V のバイポーラ型で読み取った電圧値
であるとみなしたとき、それぞれの手法で読み取った電圧値の最小値と最大値を画面に出力するプログラムを作成せよ。
- ファイル名は 11_1.cpp とする。
- ファイル名はプログラム内で指定すること。
- 電圧値は小数第3位まで表示すること。
- 参考としてそれぞれの手法で読み取った電圧値のグラフを示す。
  
  ユニポーラ型で読み取った場合
  バイポーラ型で読み取った場合
下図に示す暗号(Te st)を解読し、画面に表示せよ。
- 解読にあたり、プログラムは用いなくても構わない。
- 解読に成功すると、見覚えのある文章が出てくる。解読する手段は、第11回の中で取り組んできた内容を参考にするとよい。Asciiコード表は使うことになると思います。
- 課題2の結果は、11_1.cpp のプログラムを利用して解答せよ。以下の例のように、課題1の結果表示に続けて、課題2の解答をprintf()にて表示するようにすること。解読にプログラムを利用した場合でも、プログラムは提出しないこと。

第11回 バイナリデータ・ビット演算・データ計測