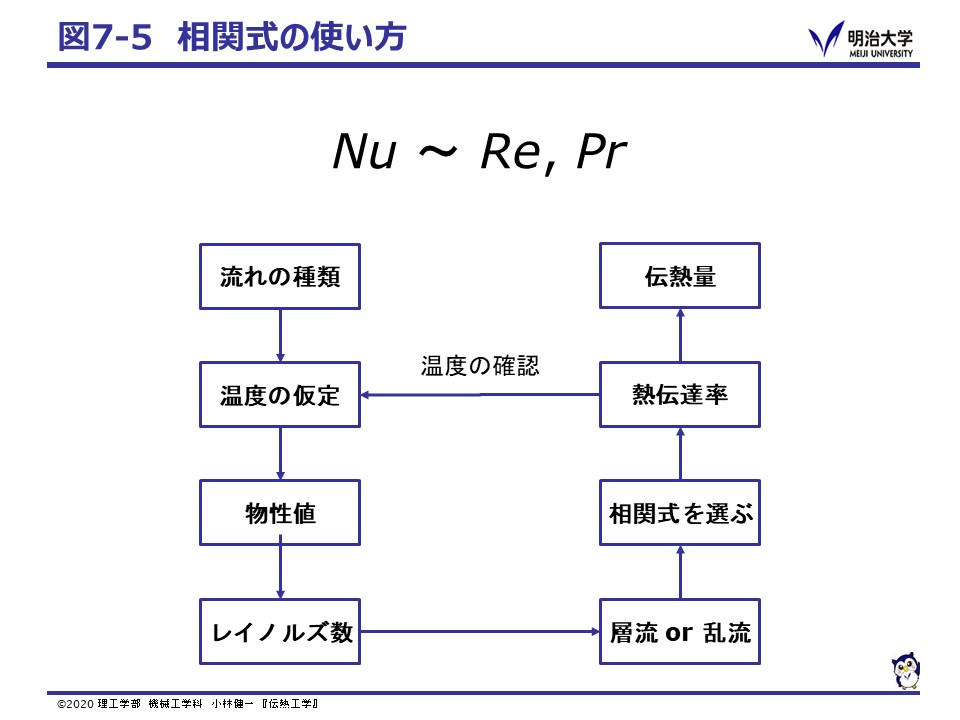
熱伝達率を求めるためには,流れの状態を把握する必要がありますが,そのためには流れの運動方程式(ナビエ・ストークスの方程式)を解かなくてはなりません。 流れの運動方程式を解析することは,計算機の発達した現在でも大きな計算負荷が必要で簡単ではありません。 そこで,いくつかの代表的な状況について,熱伝達率の無次元数と流れの状態を表す無次元数との関係式(相関式)が提供されています。
相関式を用いて熱伝達率を求める手順の概略は次の様になります。

長さ 200 mm,幅 100 mm の平板に沿って温度 Te = 20 ℃,常圧の空気が 8 m/s で流れている。 平板の温度が Tw = 100 ℃ 一定の時,この面からの伝熱量を求めよ。
平板に沿う速度/温度境界層は,平板先端から発達するが,面全体での伝熱量を求めるので,各無次元数の代表長さには平板の長さを用いる。
物性値を求めるための温度は,平板と空気の温度の平均,膜温度(Film temperature)(Tf )を用いる。
Tf における流体(空気)の物性値は,
平板全長におけるレイノルズ数は,
Re < 5.0 ×105 なので,流れは層流。壁温一定の平板の層流の平均ヌセルト数の式は,
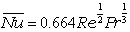 = 171.0
= 171.0
平均熱伝達率は,
したがって,伝熱量は,
長さ 50 mm,幅 50 mm の平板に沿って温度 Te = 20 ℃,常圧の空気が 8 m/s で流れている。 平板が発熱量 Q = 10 W 一定で加熱されている時,この面で最も高温となる場所の温度を求めよ。
発熱量が一定という場合,平板全体が一様に加熱されていると考え,熱流束が一定と考える。
平板に沿う温度境界層は平板先端から発達するので,最も高温となるのは流れの下流端となる。
そこで,各無次元数の代表長さには平板の長さを,また物性値を求めるための温度は,高温の箇所における膜温度を用いる。
ここで問題となるのが,等温平板の場合と異なり壁面の温度 Tw が不明な点である。
等熱流束加熱の場合は,壁温を仮定して進め最後に確認を行う必要がある。
では,Tw = 100 ℃ と仮定して計算を始めよう。
Tf における流体(空気)の物性値は,
平板後端におけるレイノルズ数は,
Rex < 5.0 ×105 なので,流れは層流。 等熱流束で加熱される平板の層流の局所ヌセルト数の式は,
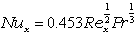 = 58.33
= 58.33
局所熱伝達率は,
したがって,下流の壁面温度は,
求まった温度(140 ℃)と,最初に仮定した温度(100 ℃)は,大きく離れているので,最初に戻って,壁温を 140 ℃ と仮定し直して,再度物性値から計算をやり直す。 途中計算は省略するが,二回目の計算結果は,
となり,仮定した温度と大きく離れていないので,これを解とする。
このような繰り返し計算には,前回演習で解説したエクセルのゴールシーク機能を活用すると便利です。
流れの中に置かれた物体が加熱されている場合の相関式を調べてまとめなさい。
例:流れに平行に置かれた加熱平板(先端から加熱)
臨界レイノルズ数:5.0×105
| 流れの状態 | 局所 代表長さ:先端からの距離 |
平均 代表長さ:板の全長 |
|---|---|---|
| 層流 | 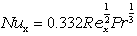 |
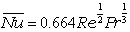 |
| 乱流 | 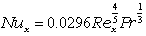 |
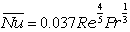 |
| 流れの状態 | 局所 代表長さ:先端からの距離 |
|---|---|
| 層流 | 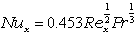 |
| 乱流 | 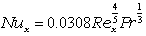 |
2021.03.08 更新