第4回　定常熱伝導

一次元定常熱伝導

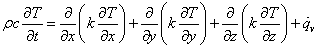
前回導出した熱伝導方程式は，時間・場所・発熱の状態が変数となり，解析により解をもとめることは不可能です。

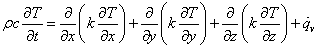
そこで，次の様な伝熱現象について考えよう。

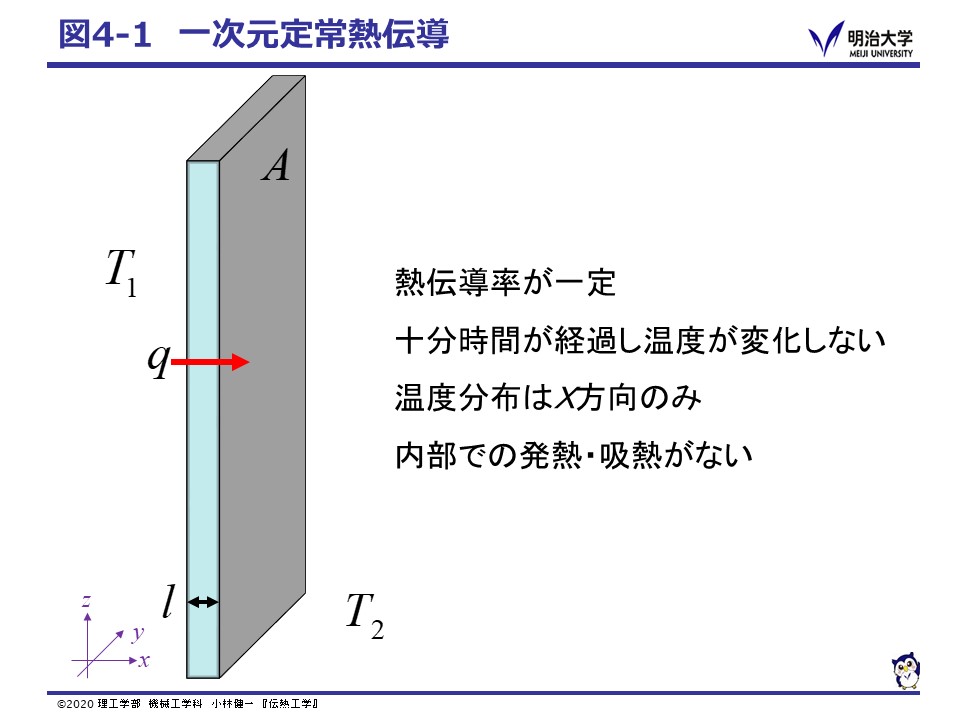
このようなケースを，一次元定常熱伝導と呼びます。 そこで，次の様な条件を満たす場合の熱伝導方程式を考えよう。

• 熱伝導率が場所によらずに一定
• 十分時間が経過し，温度分布が変化しない
• 温度が一方向にだけ変化する
• 物体内での発熱・吸熱がない

このような場合，式(1)は x 方向の温度勾配のみになり，偏微分から全微分へと変換できる。

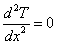
境界条件は，

　　　　　x = 0 で，T = T₁
　　　　　x = L で，T = T₂

であるから，熱流束および伝熱量はそれぞれ次の様に求まる。

円筒座標

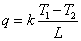
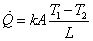
水筒の様な円筒の内部と外部の伝熱も，上記の条件が当てはまり，一見三次元に見える現象だが一次元の熱伝導問題として考えられる。

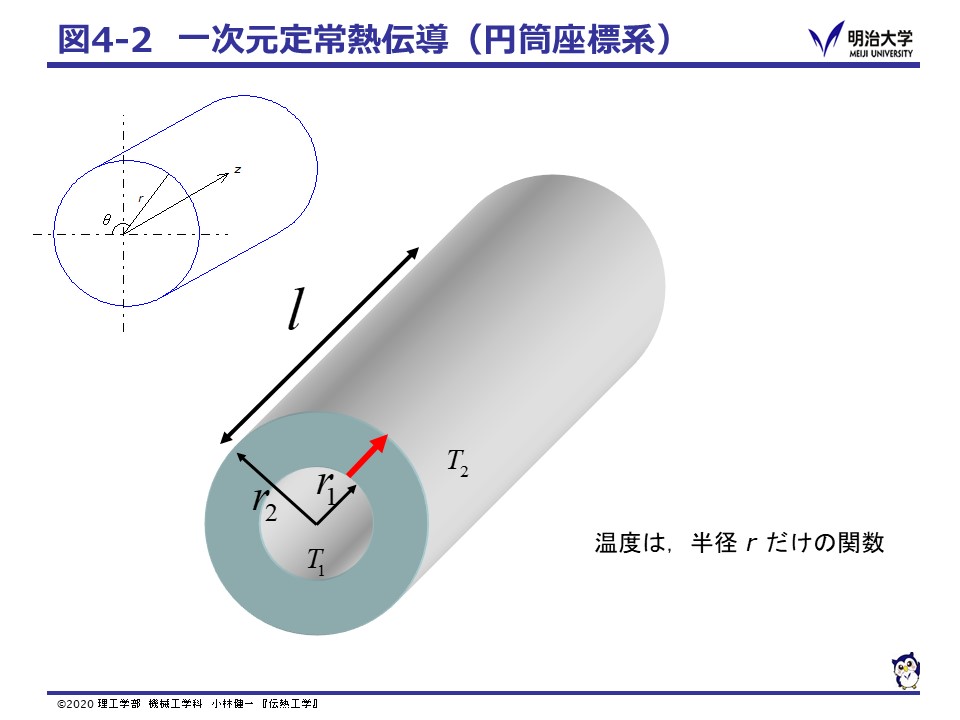
円筒座標系の熱伝導方程式

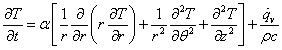
は，このような場合，r 方向の温度勾配のみとなり，全微分の方程式となる

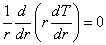
境界条件は，

　　　　　r = r₁ で，T = T₁
　　　　　r = r₂ で，T = T₂

であるから，熱流束および伝熱量はそれぞれ次の様に求まる。

今週の課題

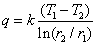
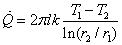
図4-3に示したように，厚さ，熱伝導率とも異なる平板が２枚重なっている。 定常状態で両端の温度が T₁, T₂ のとき，以下の問いに答えなさい。

1. 両平板の境界の温度 T_m を求めなさい。
2. 単位時間・単位面積あたりの熱流束 q を， T_m を使わないで求めなさい。

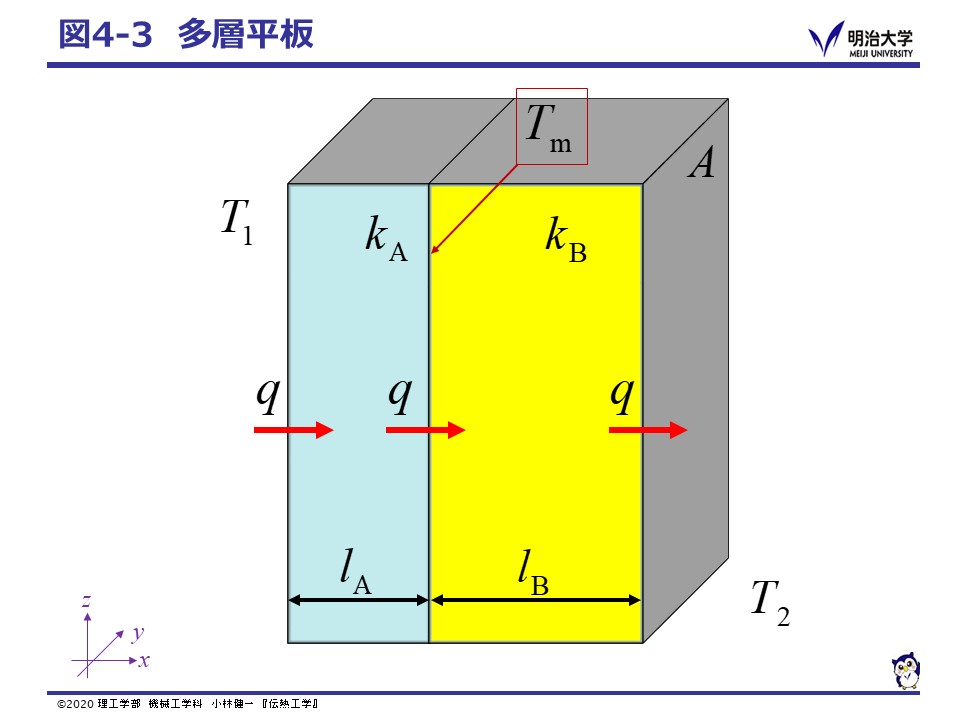
ヒント：平板が密着している場合，それぞれの平板を通過する熱流束 q は等しい。