Domain Coloring

はじめに

実関数\(f:\mathbb{R}\to\mathbb{R}\)を理解する上でグラフは非常に有用であった． それに対し，複素関数\(f:\mathbb{C}\to\mathbb{C}\)のグラフを書くのには工夫が必要である． ここでは，複素平面の各点に色を対応させることで，複素関数を視覚的に捉えるDomain Coloringについて簡単に紹介する． 詳細はインターネットで検索して調べて欲しい．

各点に色を与える

実軸が\(-5\)から\(5\)，虚軸が\(-5i\)から\(-5i\)となるガウス平面にそれぞれ以下のように点を対応させる． 色はHSV色空間(色相，彩度，明度，Hue, Saturation, Lightness)であらわし， \[H=\mathrm{arg}(z)\mod 2\pi,\ S=1-\exp(-|z|),\ V=1\] とする．

require(ggplot2)

## Loading required package: ggplot2

display <- function(f){
  z <- as.vector(outer(seq(-5, 5, by =.01),1i*seq(-5, 5, by =.01),'+'))
  fz <- f(z)
  z_color <- data.frame(x=Re(z),
              y=Im(z),
              h=Arg(fz)/(2*pi)+ifelse(Arg(fz)>=0,0,1),
              s=1-exp(-Mod(fz)),
              v=1)
  z_color <- z_color[is.finite(apply(z_color,1,sum)),]
  opt <- theme(legend.position="none",
          panel.background = element_blank(),
          panel.grid = element_blank(),
          axis.ticks=element_blank(),
          axis.title=element_blank(),
          axis.text =element_blank())
  p <- ggplot(data=z_color, aes(x=x, y=y)) + geom_tile(fill=hsv(z_color$h,z_color$s,z_color$v)) + opt
  print(p)
}

f <- function(z){z}
display(f)

関数\(f:\mathbb{C}\to\mathbb{C}\)に対し， 各点\(z\)での色を，\(f(z)\)の値の色で塗ることにする． 例えば， \[f(z)=z^2\] の場合，以下のようになる．色が2周していることが分かるだろう．

f <- function(z){z^2}
display(f)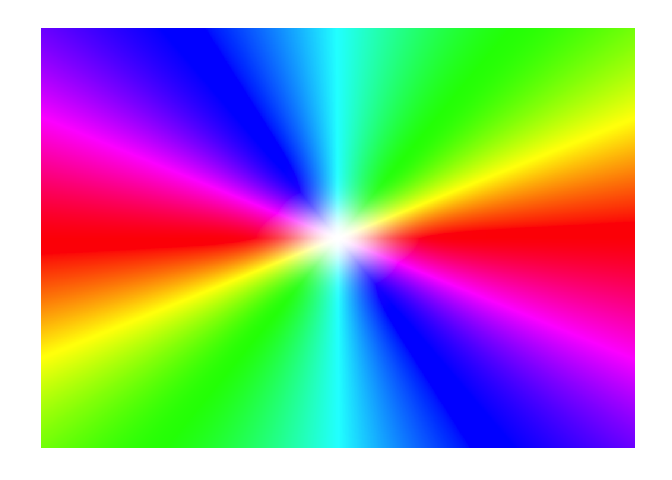

その他，代表的な関数を見てみよう．

f <- function(z){z^3}
display(f)

f <- function(z){z^4}
display(f)

f <- function(z){z^2*(1+1i)+2+3i}
display(f)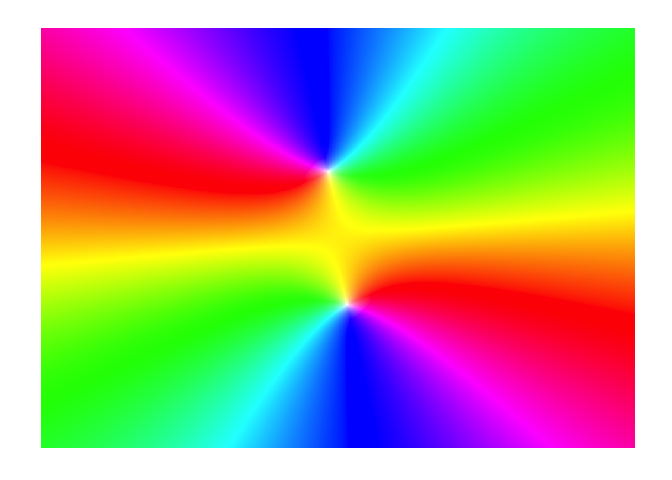

f <- function(z){10/(z^2+1)}
display(f)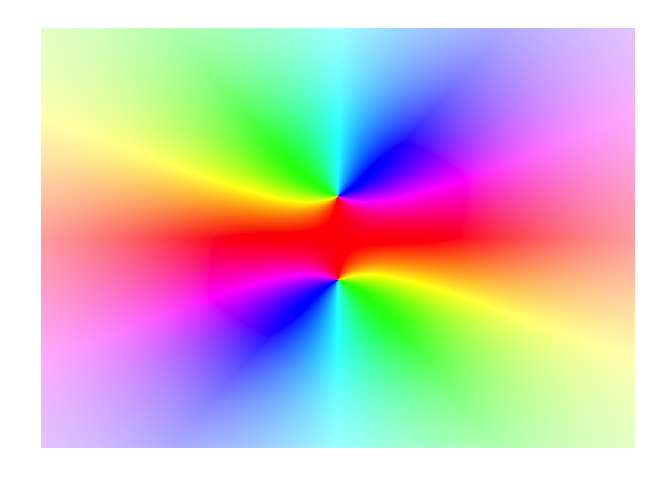

f <- function(z){(z^2+10)/(z^2-10)}
display(f)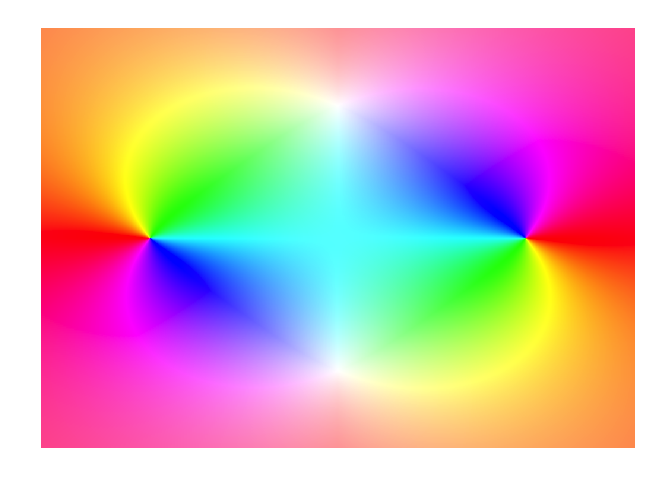

f <- function(z){exp(z)}
display(f)

f <- function(z){log(z)}
display(f)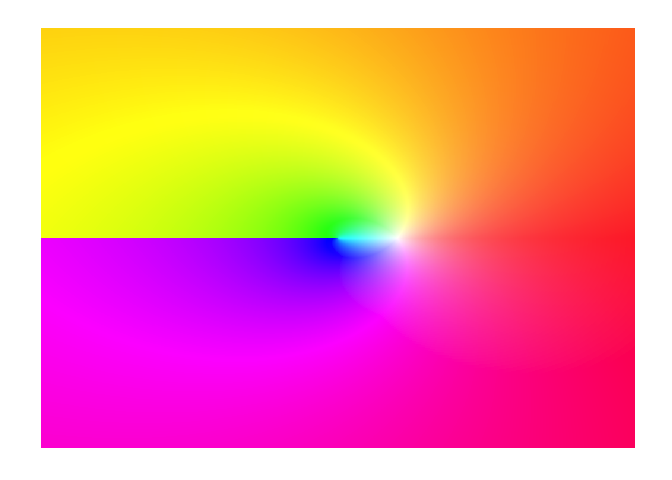

f <- function(z){sin(z)}
display(f)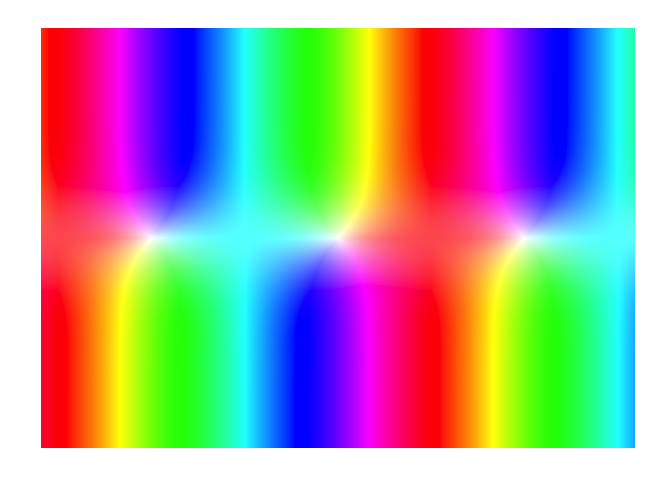

f <- function(z){sinh(z)}
display(f)

f <- function(z){tan(z)}
display(f)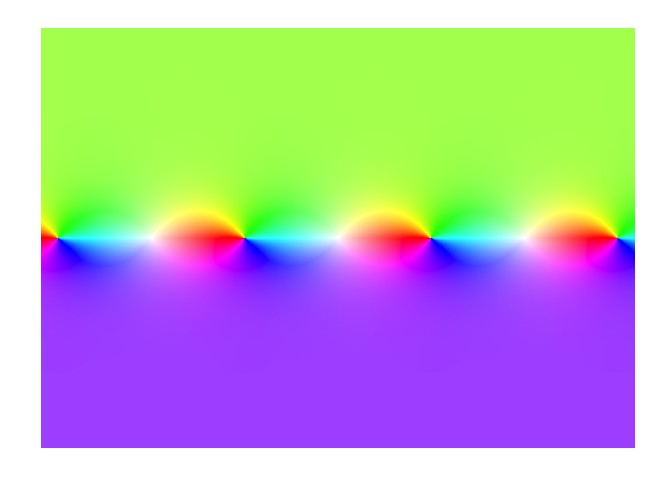

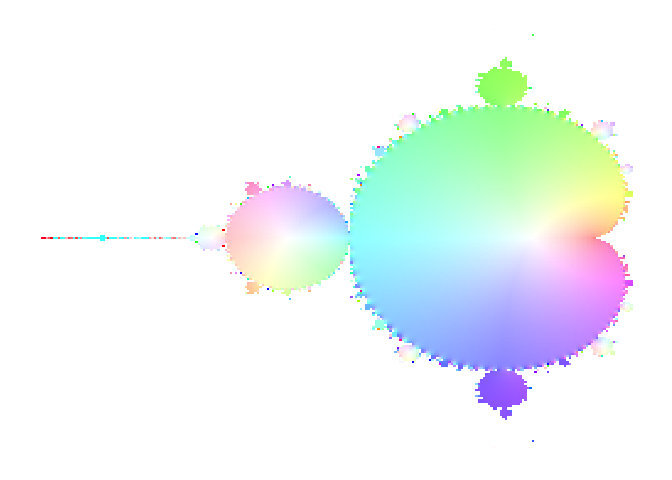
以下は繰り返しを100回で止めたときのマンデルブロー集合である．

f <- function(z){
  w <- 0
  for(i in 1:100){
    w <- w^2+z
  }
  w
}
display(f)