1 2次元拡散方程式

\(t,x,y\) の関数 \(u=u(x,y,t)\) についての方程式 \[\begin{align*} \frac{ \partial u}{\partial t}=a\left(\frac{\partial^2u}{\partial x^2} + \frac{\partial^2u}{\partial y^2}\right)\ \ \ (0\leq x \leq 1 ,0\leq y \leq 1 , 0 \leq t) \end{align*}\] は2次元拡散方程式と呼ばれている。これは\(1\times 1\)の領域における熱の伝わり具合を表す方程式である。 このレポートでは、熱の分布を色によって視覚化し、その変化の様子を動画にする。

数値計算によってこの方程式の解を求めるために、まずは離散化を行う。

\[\begin{align*} \frac{u(x,y,t+Δt)-u(x,y,t)}{Δt} =& a\left(\frac{\partial}{\partial x}\left(\frac{u(x+Δx,y,t)-u(x,y,t)}{Δx}\right) + \frac{\partial}{\partial y}\left(\frac{u(x,y+Δy,t)-u(x,y,t)}{Δy}\right)\right)\\ =& a\left(\left(\frac{u(x+Δx,y,t)-2u(x,y,t)+u(x-Δx,y,t)}{(Δx)^2}\right) + \left(\frac{u(x,y+Δy,t)-2u(x,y,t)+u(x,y-Δy,t)}{(Δy)^2}\right)\right)\\ u(x,y,t+Δt) =& u(x,y,t)+aΔt\left(\left(\frac{u(x+Δx,y,t)-2u(x,y,t)+u(x-Δx,y,t)}{(Δx)^2}\right) + \left(\frac{u(x,y+Δy,t)-2u(x,y,t)+u(x,y-Δy,t)}{(Δy)^2}\right)\right) \end{align*}\]

安定性条件は下である。 \[\begin{align*} aΔt\left(\frac{1}{(Δx)^2}+\frac{1}{(Δy)^2}\right)\leq\frac{1}{2} \end{align*}\]

2 シミュレーション

下のように、座標、時間を離散化する。

a <- 0.2

J <- 30  #x座標の離散化
K <- 30  #y座標の離散化
dx <- 1/J
dy <- 1/K

Tmax <- 1　#1秒間で考える
N <- 800  #時間の離散化
dt <- Tmax/N

u<- array(NA,dim=c(J+1,K+1,N+1))  #u=u(x,y,t)として3次元の配列を用意する

a*dt*(1/dx^2 + 1/dy^2)

## [1] 0.45

この設定は安定性条件を満たしていることが分かる。

初期状態 \(t=0\) の値は、\(x+y \leq 1\) を満たす範囲では\(x+y\)、\(x+y > 1\) の範囲では\(2 - (x+y)\) と定めた。

for(j in 0:J){
  for(k in 0:K){
     u[j+1,k+1,1] <- ifelse(j*dx+k*dy<=1,j*dx+k*dy,2-(j*dx+k*dy))
  }
}

\(t>0\) については離散化した方程式を用いて値を求める。 境界は一定値をとると定めた。

for(n in 1:N){
  for(k in 0:K){
    for(j in 0:J){
      #境界は一定値
      u[1,k+1,n+1] <- u[1,k+1,n]    
      u[J+1,k+1,n+1] <- u[J+1,k+1,n]
      u[j+1,1,n+1] <-  u[j+1,1,n]
      u[j+1,K+1,n+1] <- u[j+1,K+1,n] 
    }
  }
  
  for(j in 1:(J-1)){
    for(k in 1:(K-1)){
        u[j+1,k+1,n+1] <- u[j+1,k+1,n] + a^2*dt*(( u[j,k+1,n] - 2*u[j+1,k+1,n] + u[j+2,k+1,n] )/dx^2
                                                 +( u[j+1,k,n] - 2*u[j+1,k+1,n] + u[j+1,k+2,n] )/dy^2)
    }
  }
}

初期状態は下のような分布である。

image(-u[,,1],col=heat.colors(100))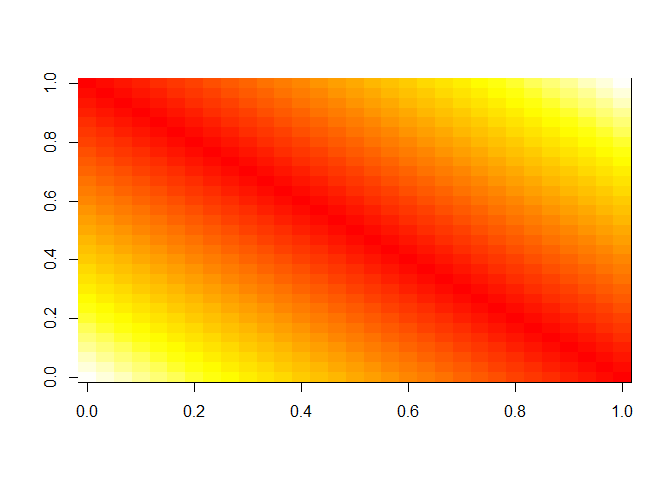

library(knitr)

## Warning: package 'knitr' was built under R version 3.2.5

opts_knit$set(animation.fun = hook_scianimator)

動画が下である。 繰り返し回数が\(\frac{N}{50}i(i=0,1,,50)\)回の時の画像をつなげて表示している。

n <- 50
m <- N/n

for(i in 0:n){
  image(-u[,,1+m*i],col=heat.colors(100))
}

このように、熱が均一化されていく様子が見て取れる。