素数とサイコロ
秋山 昌晴
2015/11/17
## Warning: package 'knitr' was built under R version 3.1.31 テーマ
通常の六面体のサイコロを考える. ここで, どの目が出ることも同様に確からしいと仮定する. このサイコロを何回か投げたとき, それらの目の和が素数になる確率を考える.
1.1 設定
サイコロを \(n\) 回投げる. このとき, 出た目の和を \(S_n\) とする. また, \(S_n\) が素数となる確率を \(P_n\) とする.
1.2 例
\(n = 1\) のとき, \(1 \leq S_1 \leq 6\) である. \(1\) 以上 \(6\) 以下の素数は \(2, 3, 5\) の \(3\) 個なので \[ P_1 = \dfrac{3}{6} = \dfrac{1}{2} \] となる. \(n = 2\) のとき, \(2 \leq S_2 \leq 12\) である. \(2\) 以上 \(12\) 以下の素数は \(2, 3, 5, 7, 11\) の \(5\) 個で, \(S_2\) がこれらの値をとるのはそれぞれ \(1, 2, 4, 6, 2\) 通り. よって \[ P_2 = \dfrac{1+2+4+6+2}{6^2} = \dfrac{15}{36} = \dfrac{5}{12} \] となる.2 シミュレーション
2.1 準備
正の整数 \(x\) に対して, 関数 \(d(x)\) を次で定める ; \[ d(x) := \begin{cases} 1 \quad (\ x\,は素数\ )\\ 0 \quad (\ x\,は素数ではない\ ) \end{cases} \]
# エラトステネスのふるいで十分素数を計算しておく
cal_primes <- function(n){
r <- rep(TRUE,n)
r[1] <- FALSE
for(i in 2:(floor(sqrt(n))+2)){
if((r[i] == TRUE) && (( q <- n %/% i) > 1)){
for(j in 2:q){ r[i*j] <- FALSE }
}
}
return(r)
}
xmax <- 12
primes <- cal_primes(xmax)
d <- function(n){
if(primes[n]){return(1)}else{return(0)}
}実際に \(x = 1, 2, \cdots , 12\) に対する \(d(x)\) の値を見る.
plot(primes,
pch = 19, main = "prime number",
xlab = "x", ylab = "d(x)",
xlim = c(1, xmax), ylim = c(0, 1.2),
xaxp = c(1, xmax, xmax - 1), yaxp = c(0, 1, 1),
panel.first = (abline(v = 1:xmax, h = 0:1, lty = 2, col = "#E9DECA"))
)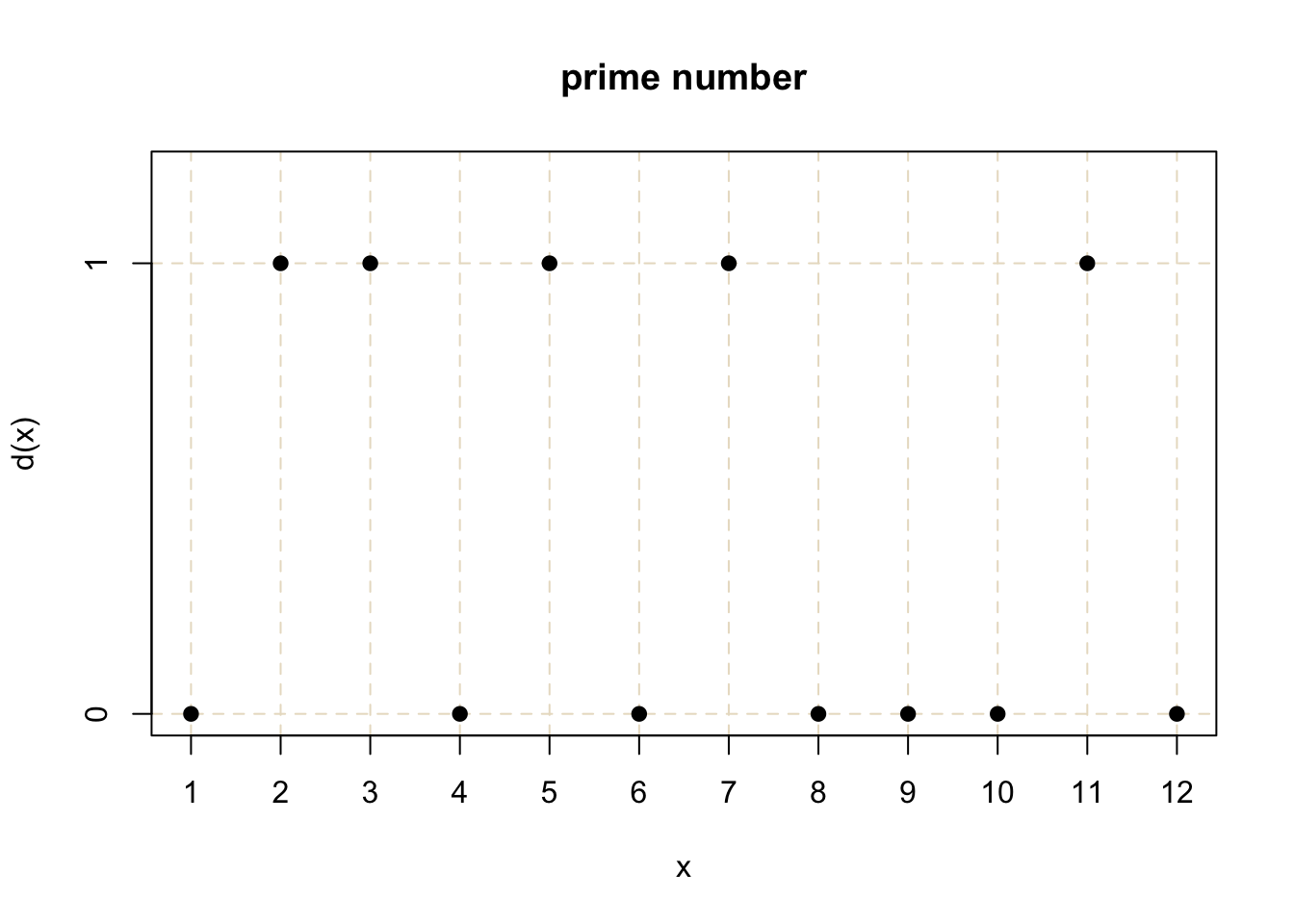
\(x\) が素数である \(2, 3, 5, 7, 11\) のとき \(d(x) = 1\) (TRUE), その他の場合には \(d(x) = 0\) (FALSE) となっていることがわかる.
2.2 設定
今回は, サイコロを投げる回数 \(n\) を \(1 \leq n \leq nmax = 5 \times 10^2\) の範囲で検証する. また, このシミュレーションによって得る確率を \(p_n\) (\(n = 1, 2, \cdots, nmax\)) とおく.
m <- 6 # 面の数
nmax <- 5*10^2 # サイコロを投げる回数
tmax <- 10^4 # 試行回数
s.s. <- 6 # シード
#後で使うので十分大きな素数まで計算しておく
primes <- cal_primes(50*10^2)2.3 実行
関数 \(d(x)\) を用いて, 確率 \(p_n\) を求める.
set.seed(s.s.)
data1 <- floor(runif(tmax*nmax, 1, m+1)) # サイコロの目(データ)の列
# 各行が試行1回分のデータとなる tmax*nmax 行列
Dice1 <- matrix(data1, nrow = tmax, ncol = nmax)
# Sum1のj列をDice1のj列までのデータの和(累積和)とする
Sum1 <- t(apply(Dice1, 1, cumsum))
# Sum1の各成分に関数dを適用
Prime1 <- apply(Sum1, c(1, 2), d)
# Prime1の各列の平均を求める
# 求めた(nmax個の)値が求める確率となる
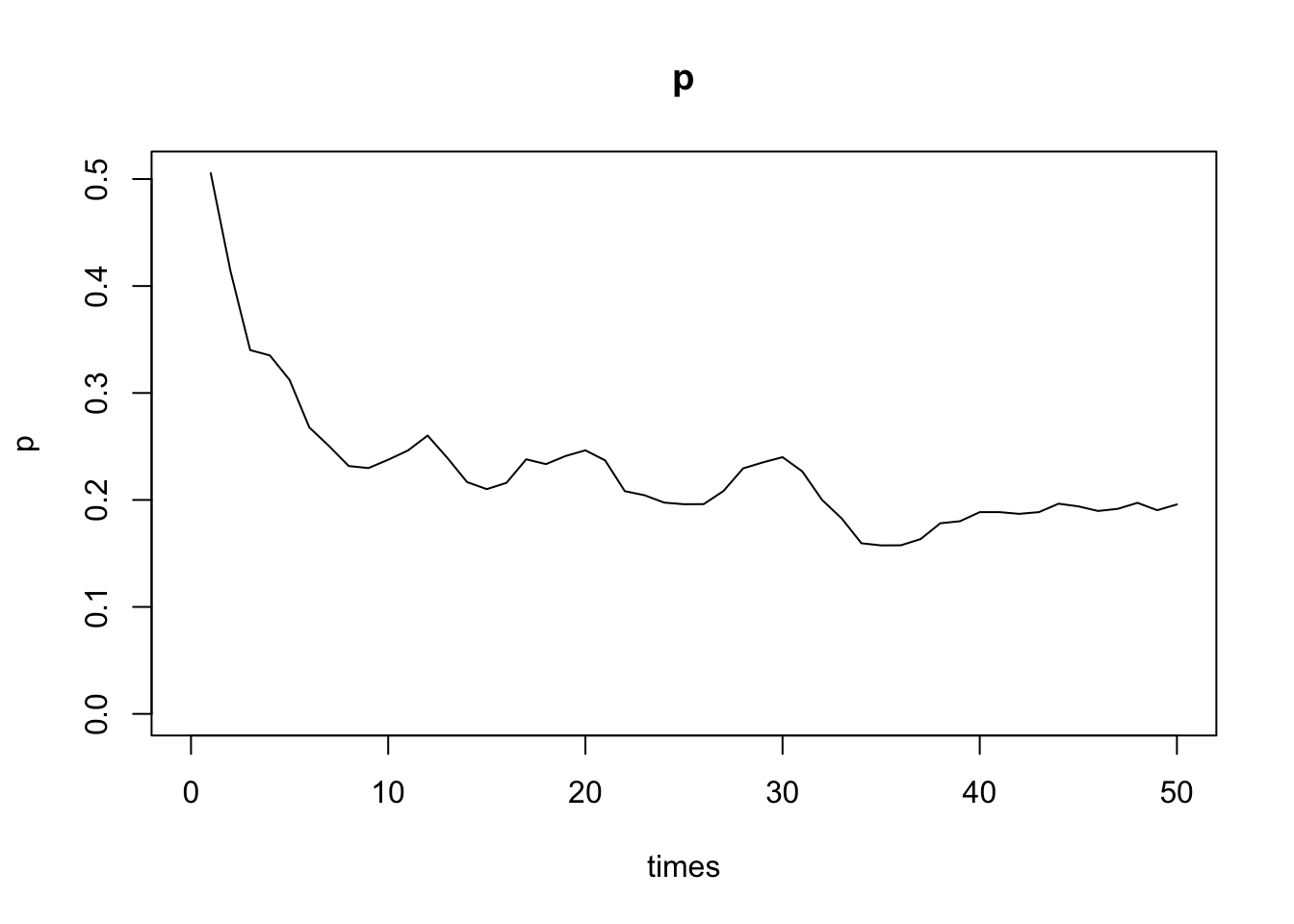
p <- apply(Prime1, 2, mean)サイコロを投げる回数 \(n\) に対する確率 \(p_n\) の変化を見る.
plot(p[1:50],
main = "p", type = "l",
xlab = "times", ylab = "p",
xlim = c(0, 50), ylim = c(0, max(p))
)
dn <- 60 # plotするグラフの分割数(枚数)
for(k in seq(0, nmax, nmax %/% dn)){
plot(p[1:k],
main = "p", type = "l",
xlab = "times", ylab = "p",
xlim = c(0, nmax), ylim = c(0, max(p))
)
}2.4 確認
計算によって求めた確率 \(P_1 = \dfrac{1}{2}, P_2 = \dfrac{5}{12}\) を, シミュレーションによって求めた確率 \(p_1, p_2\) と比較する. 次の値を出力する; \[ \left( P_1 ,\ p_1 \right),\quad \left( P_2 ,\ p_2 \right) \]
c(P[1], p[1])[1] 0.5000 0.5055c(P[2], p[2])[1] 0.4166667 0.4140000また, \(n = nmax = 5 \times 10^2\) のときの確率 \(p_{nmax}\) は次の値となる.
p[nmax][1] 0.13172.5 観察
これまで, 通常の六面体のサイコロを投げる場合を考えてきた. 今, \(1 \leq m \leq mmax = 50\) に対して, どの目が出ることも同様に確からしい \(m\) 面体のサイコロがあると仮定する. 前に見た「サイコロを投げる回数 \(n\) と確率 \(p_n\) の関係」が 面の数 \(m\) の値によってどう変化するかを見る.
ここで, \(m\) 面体のサイコロを \(n\) 回投げたとき, 目の和を \(S_{m, n}\) とし, このシミュレーションによって得る確率を \(q_{m, n}\) とする.
mmax <- 50 # 面の数の最大値
nmax2 <- 10^2 #サイコロを投げる回数
#前にすでに計算したので省略
#primes <- cal_primes(mmax*nmax2)
# i面体によるj回目の試行において, k回目に出た目を(i,j,k)成分とする3次元配列
# 各iに対して, Dice2の成分は tmax*nmax2 行列をなす
Dice2 <- array(NA, dim=c(mmax, tmax, nmax2))
for(i in 1:mmax){
set.seed(s.s.) ; data2 <- floor(runif(tmax*nmax2, 1, i+1))
Dice2[i,,] <- matrix(data2, nrow = tmax, ncol = nmax2)
}
# 次のSum2, Prime2, qは, 各iに対応するtmax*nmax2行列に対して, Sum1, Prime1, pと同じ操作をすることで得る
Sum2 <- aperm(apply(Dice2, c(1, 2), cumsum), perm=c(2, 3, 1))
Prime2 <- apply(Sum2, c(1, 2, 3), d)
q <- apply(Prime2, c(1, 3), mean)一方で, ガウスの素数定理 より, 十分大きな整数 \(X\) が素数である確率は次の関数で近似できることが知られている ; \[ N_p (X) := \frac{1}{\log X} \] また, \(m\) 面体のサイコロを \(n\) 回投げたとき, 目の和 \(S_{m, n}\) の期待値は \[ E\left( S_{m, n} \right) = \frac{m+1}{2} \times n \] となる. この \(2\) 式より, 次の関数を定める ; \[ app(m, n) := N_p \left( E\left( S_{m,n} \right) \right) = \frac{1}{\log \dfrac{(m+1)n}{2}} \]
app <- function(m, n){
return( 1/log(n*(m+1)/2) )
}各 \(m = 1, 2, \cdots, mmax\) について \(q_{m, n}\) と \(app(m, n)\) の値をplotする.
for(K in 1:mmax){
plot(app(K, 1:nmax2),
ann = F, type = "l", col = "red", lwd = 2.5,
xlim = c(0, nmax2), ylim = c(0, 1)
)
par(new=T)
plot(q[K, 1:nmax2],
main = K, type = "l", col = "black", lwd = 1.5,
xlab = "times", ylab = "",
xlim = c(0, nmax2), ylim = c(0, 1)
)
legend("topright",
legend=c("q", "app"),
col = c("black", "red"),
lwd = c(1.5, 2.5),
lty = 1
)
}elapsed
205.466