Maxwell-Boltzmann統計,Fermi-Dirac統計,Bose-Einstein統計など、 それぞれ統計により、エネルギーに対する粒子の分布関数が異なる。 しかし、なぜそれぞれの分布関数が異なるのか、直感的には理解できないと思う。 そこで、それぞれの統計に対応した分布関数が、どのように導出されるのかを、 以下にまとめた。 この解説の作成にあたり、以下の文献を参考にした。
外部から仕事が成されなければ、物事はエネルギーの低い状態に、
自発的に変化していく。
例えば、坂道にボールを静かに置くと、ボールは自発的に坂道を転がり落ちていく。
位置エネルギーの低い状態に変化していくわけだ。
一方で、テーブルの上の水滴は、加熱(外部からの仕事)をせずとも、
自発的に蒸発する。
ところが、水が蒸発するには、気化熱というエネルギーが必要である。
水の気化熱は摂氏25度1気圧で、2,267 [J/g]である。
水分子の間には引力が働いているから、液体という分子同士が密着した状態にある。
それが密度の低い気体になるには、
密着していた分子同士を、引き離すエネルギーが必要となる。
となると、水滴が蒸発する現象は、
自発的にエネルギーの高い状態へと変化する現象なのであろうか?
そう考えてはならない。
気化熱などの「分子間の相互作用エネルギー」に関する量は、
エンタルピー\(H\)であらわされる。
上記の議論では、エンタルピーしか考えなかったため、
矛盾を生んだ。実は、エントロピー\(S\)に関係するエネルギーも、
同時に考慮しなければならない。
エントロピーとは、直感的には「乱雑さの程度」を表す量で、
「乱雑さの程度」が増すと、エントロピーの値が増す。
多数の分子の集団的な状態変化を考えるときには、
エンタルピーとエントロピーを考慮した、
ギプスの自由エネルギー\(G\)を用いると便利である。
ギプスの自由エネルギー\(G\)は、
\begin{align}
G=H-TS
\label{eq:G}
\end{align}
で与えられる。
水滴の蒸発前後のギプスの自由エネルギーの差(\({\it \Delta}G\))を、温度一定のもとで考える。
\begin{align}
G_{\text{蒸発後}}-G_{\text{蒸発前}}={\it \Delta}G={\it \Delta}H-T{\it \Delta}S
\label{eq:dG}
\end{align}
\({\it \Delta}G < 0\)であれば、
自発的に状態が変化する(状態変化後にエネルギーが下がる)現象である。
水滴が蒸発するとき、
分子間相互作用エネルギーのみを考えると、
式\(\eqref{eq:dG}\)の\({\it \Delta}H > 0\)であるが、
\({\it \Delta}S\)はどうだろうか?
多数の水分子が密に接した液体よりも、
気化して酸素や二酸化酸素ガスなどど混ざった方が、
乱雑さの程度は増すであろう(\({\it \Delta}S > 0\))。
その結果、\({\it \Delta}H < T{\it \Delta}S\)となり、
水滴が蒸発する現象は、自発的に起きる現象(\({\it \Delta}G < 0\))なのである。
従って、「集団的な」物事の状態を考えるときには、
エントロピー\(S\)に関するエネルギー(\(-TS\))も考慮に入れる必要がある。
温度一定の場合、式\(\eqref{eq:G}\)から、物事が自発的に変化する場合は、
エントロピー\(S\)が最大になる状態(\(TS\)を最大にして\(G\)を最小にする状態)に向かって物事が変化していくこととなる。
そして、対象としている集団(系)が、熱平衡状態にあるとき、
その系は、エントロピーが最大になるような状態をとる。
系を巨視的に見るか、微視的にみるかで、具体的なエントロピーの表式は異なる。
巨視的に系を見る場合、その系に加えられた熱量の変化を\({\it \Delta}Q\)とすると、
それによって引き起こされる、エントロピー変化は、
\begin{align}
{\it \Delta}S=\frac{{\it \Delta}Q}{T}
\label{eq:Smacro}
\end{align}
で表される。
水滴の蒸発の場合、周囲から奪った気化熱の分が、
\({\it \Delta}Q\)に対応する。
分子を個々の粒子とみる微視的な立場でのエントロピーは、ボルツマンの公式で与えられる。
\(k_{\text{B}}\)をボルツマン定数として、
\begin{align}
S=k_{\text{B}}\ln W
\label{eq:Smicro}
\end{align}
で表記する。ここで\(W\)は、系が取りうる状態の「場合の数」である。
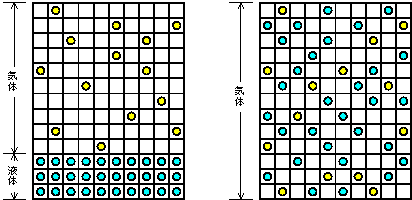
Fig.1の簡単な図において、気化前は、液体の領域では分子の配置の仕方は1通りしかなく、
気体の領域では、もともと気体であるガス分子によって占められている。
液体が気化すると、もともとのガス分子との混合が起き、分子の配置の仕方の「場合の数」が増加する。
従って気化後、エントロピーが増大することが容易に想像できるであろう。
以下に、微視的な立場から、いろいろな性質をもった粒子の集団が、エネルギーに対してどう分布するのかを解説する。
 |
| Fig.1: 気化前後における分子の配置の違い. |
この統計が対象とする粒子は、「個々の区別がつき、 いくらでも同じエネルギーをとることができる」性質を持ていることが前提である。 便宜的にとりうるエネルギーは、 \begin{align} \varepsilon_{i},~(i = 1,~2,~\cdot~\cdot~\cdot) \label{eq:ei} \end{align} のように離散的であるとする。ただし、その間隔は非常に狭い。 上述した性質の粒子が、各エネルギー準位(\(\varepsilon_{i}\))に、 どう配置されるかをFig.2に示した。 全粒子数が\(N\)個あり、その中から\(n_{1}\)個の粒子を取り出して、 エネルギー準位\(\varepsilon_{1}\)に配置する場合の数\(W_{1}\)を考える。 \(N\)個の中から\(n_{1}\)個の粒子を取り出す場合の数は、 \begin{align*} N \times (N-1) \times (N-2) \times~\cdot~\cdot~\cdot~\times (N-n_{1}+1) = {}_{N}\text{P}_{n_{1}} \end{align*} 通りである。 取り出した\(n_{1}\)個の粒子を、どのような順番で\(\varepsilon_{1}\)に配置するかは問わないので、 \(\varepsilon_{1}\)に配置する場合の数\(W_{1}\)は、 \begin{align*} W_{1} = \frac{{}_{N}\text{P}_{n_{1}}}{n_{1}!} = {}_{N}\text{C}_{n_{1}} \end{align*} となる。 エネルギーの一番低い\(\varepsilon_{1}\)から順に粒子を配置していくと、 Table 1のように各\(\varepsilon_{i}\)に対する場合の数\(W_{i}\)が求まる。
|
|
従って、\(N\)個全ての粒子を、各エネルギー状態に分配する場合の数\(W\)は、 \begin{align} W = \prod_{i} W_{i} = \frac{N!}{n_{1}!n_{2}!n_{3}!~\cdot~\cdot~\cdot} \label{eq:Wb} \end{align} である。式\(\eqref{eq:Wb}\)の両辺の対数を取り、 スーターリングの公式(\(\ln(a!) \approx a (\ln a -1)\), ただし\(a\)が十分大きい)を使うと、 \begin{align} \ln W & = N \ln N - \sum_{i} n_{i} \ln n_{i} = \sum_{i} n_{i} (\ln N - \ln n_{i}) \nonumber \\ & = - N \sum_{i} \left(\frac{n_{i}}{N}\right) \ln \left(\frac{n_{i}}{N}\right) \label{eq:Wb2} \end{align} と整理できる。ここで、 \begin{align} N = \sum_{i} n_{i} \label{eq:Nb} \end{align} という関係式を用いた。また、全エネルギー\(E\)は、 \begin{align} E = \sum_{i} n_{i} \varepsilon_{i} \label{eq:Eb} \end{align} である。 ところで、系が熱平衡状態にあるとき、 系のエントロピーに関するエネルギー\(TS\)は最大でなければならなかった。 つまり、\(N\)個の粒子からなる系が熱平衡状態であれば、 系の\(TS\)が最大になるように、 各粒子が各\(\varepsilon_{i}\)に分配されなければならない。 式\(\eqref{eq:Smicro}\)より、 \(TS = k_{\text{B}}T\ln W\)が最大になるように、 式\(\eqref{eq:Wb2}\)の\(n_{i}\)と\(\varepsilon_{i}\)を決めればよい。 だたし、\(n_{i}\)と\(\varepsilon_{i}\)には、 それぞれ式\(\eqref{eq:Nb}\)と式\(\eqref{eq:Eb}\)なる制約がある。 このように、変数に制約があるもとで関数の極値を得る方法を、 ラグランジュの未定乗数法という。 関数\(\Psi\)と\(\psi_{i}\)を、未定な乗数\(\alpha\)と\(\beta\)を使って、 \begin{align} \Psi & = k_{\text{B}}T\ln W - \alpha N - \beta E \label{eq:Lagb} \\ & = k_{\text{B}}T \left( - N \sum_{i} \left(\frac{n_{i}}{N}\right) \ln \left(\frac{n_{i}}{N}\right) \right) - \alpha \sum_{i} n_{i} - \beta \sum_{i} n_{i} \varepsilon_{i} \nonumber \\ & = \sum_{i} \left( - k_{\text{B}}T n_{i} \ln \left(\frac{n_{i}}{N}\right) - \alpha n_{i} - \beta n_{i} \varepsilon_{i} \right) \nonumber \\ & = \sum_{i} \psi_{i} \nonumber \end{align} のように定義すると、\(k_{\text{B}}T\ln W\)の極大値を与える\(n_{i}\)は、 \(\partial \psi_{i} / \partial n_{i} = 0\)を満足する。 \(i\)番目の場合について、計算すると、 \begin{align} - k_{\text{B}} T \ln \left( \frac{n_{i}}{N} \right) - k_{\text{B}} T - \alpha -\beta \varepsilon_{i} = 0 \label{eq:Lagbi} \end{align} となり、 \begin{align} \frac{n_{i}}{N} = \exp \left( - \frac{k_{\text{B}} T + \alpha +\beta \varepsilon_{i}} {k_{\text{B}} T} \right) \propto \exp \left( - \frac{\beta \varepsilon_{i}}{k_{\text{B}} T} \right) \label{eq:Lagbi2} \end{align} が得られる。ところで、外部から\({\it \Delta} Q\)の熱量が系に与えられたとき、 系が外部に一切仕事をしなければ、系の内部エネルギーの変化分\(dE\)は、 与えられた熱量に等しい(\(dE = {\it \Delta} Q\))。 一方、\({\it \Delta} Q\)の熱量を吸収したときの系の温度が\(T\)とすると、 系のエントロピー変化は、式\(\eqref{eq:Smacro}\)より、 \begin{align} dS = \frac {{\it \Delta} Q}{T} \label{eq:dS} \end{align} である。 \({\it \Delta} Q\)が非常に小さければ、 熱量吸収にともない系の内部エネルギーが変化したとしても、 \(k_{\text{B}}T\ln W\)は極大値を取り続けるだろうし、 式\(\eqref{eq:Lagb}\)で定義した\(\Psi\)も極値(\(\sum_{i} \partial \Psi / \partial n_{i} = \sum_{i} \partial \psi_{i} / \partial n_{i} = 0\))を取りながら変化するはずである。 従って、式\(\eqref{eq:Lagb}\)の全微分は、 式\(\eqref{eq:Smicro}\)と式\(\eqref{eq:dS}\)を利用して、 \begin{align} d\Psi = T dS - \beta dE = dE - \beta dE =0 \label{eq:dPsi} \end{align} となり、 \begin{align} \beta = 1 \label{eq:beta} \end{align} であることが分かる。 また、エネルギーの基準はどこにとっても構わないので、 \(k_{\text{B}}T+\alpha = - \mu\)として、 離散的にしたエネルギー\(\varepsilon_{i}\)を連続変数\(\varepsilon\)に戻すと、 エネルギー\(\varepsilon\)に配置されている粒子の分布関数\(f(\varepsilon)\)は、 式\(\eqref{eq:Lagbi2}\)より、 \begin{align} f(\varepsilon) = \exp \left( - \frac{\varepsilon-\mu}{k_{\text{B}}T} \right) \label{eq:Boltz} \end{align} となる。これが、Maxwell-Boltzmann統計が与える分布関数であり、 Boltzmann分布とも呼ばれる。\(A\)を定数として、 \(f(\varepsilon) = A \exp ( - \varepsilon / k_{\text{B}}T )\)とすることも多い。 この分布関数に従うものは、 古典力学に従って運動する原子や分子で構成された気体や液体が典型である。 分子間相互作用ポテンシャルエネルギーの下で、 分子の集団が式\(\eqref{eq:Boltz}\)の分布関数に従って振る舞うのが、 その分子の気体や液体であり、 物質にまつわる多くの現象はMaxwell-Boltzmann統計に基づいて説明できる。
式\(\eqref{eq:ei}\)のように離散的なエネルギーを考える。
Fig.3のように、各エネルギー準位\(\varepsilon_{i}\)に、
\(g_{i}\)個の縮退した(エネルギーは等しいが状態は異なる)状態があり、
そこに\(n_{i}\)個の粒子が配置されるとする。ただし、\(g_{i} > n_{i}\)である。
ここで取り扱う粒子は、
「各\(\varepsilon_{i}\)の\(g_{i}\)個の状態に1つずつしか入ることができず、
個々の粒子の区別がつかない」性質がある。
一例として、個体中の電子がこのような性質を示し、
エネルギーが等しい各状態に1つしか入れない性質は、
パウリの排他律を反映している。
そこで、エネルギー準位\(\varepsilon_{1}\)の\(g_{1}\)個に縮退した状態に、
\(n_{1}\)個の粒子を配置する場合の数\(W_{1}\)を考える。
各状態に1つしか粒子が配置されず、個々の粒子は区別がつかないので、
\(n_{1}\)個の粒子を\(g_{1}\)個の状態に分配する仕方は、
\(g_{1}\)個の状態から、\(n_{1}\)個の選び選び方の数に等しい。
従って、
\begin{align*}
W_{1} = {}_{g_{1}}\text{C}_{n_{1}}
\end{align*}
となる。\(i=1\)番目以降も同様なので、各\(\varepsilon_{i}\)の粒子の配置の場合の数\(W_{i}\)は、
Table 2のようになる。そして、\(N\)個の粒子全てを、各エネルギー準位に分配する場合の数\(W\)は、
\begin{align}
W = \prod_{i} W_{i} = \prod_{i} {}_{g_{i}}\text{C}_{n_{i}} = \prod_{i} \frac{g_{i}!}{n_{i}!(g_{i}-n_{i})!}
\label{eq:Wf}
\end{align}
となる。これが、Fermi-Dirac統計で扱う粒子集団の配置の場合の数であり、
Maxwell-Boltzmann統計の場合の場合の数(式\(\eqref{eq:Wb}\))と異なる。
この粒子の性質の違いによる粒子集団の配置の場合の数の相違が、
それぞれの統計で異なる分布関数を用いる要因である。
|
|
\(W\)が求まったので、\(k_{\text{B}} T \ln W\)を最大にする、 各\(\varepsilon_{i}\)に対する\(n_{i}\)の関係式を求めれば、 それをFermi-Dirac統計が与える分布関数となる。式\(\eqref{eq:Wf}\)の両辺の対数を取り、 スターリングの公式(ただし、\(n_{i},~g_{i}, g_{i}-n_{i}\)は十分大きい)を用いてまとめると、 \begin{align} \ln W &= \ln \left( \prod_{i} \frac{g_{i}!}{n_{i}!(g_{i}-n_{i})!} \right) \nonumber \\ &= \sum_{i} \frac{g_{i}!}{n_{i}!(g_{i}-n_{i})!} \nonumber \\ &= \sum_{i} \left( g_{i} \ln g_{i} - n_{i} \ln n_{i} - (g_{i}-n_{i})_{i} \ln (g_{i}-n_{i}) \right) \label{eq:Wf2} \\ &= \sum_{i} W_{i} \ln W_{i} \nonumber \end{align} となる。式\(\eqref{eq:Lagb}\)と同様に\(\Psi\)を定義して、 ラグランジュの未定乗数法により、\(k_{\text{B}} T \ln W\)を最大にする\(\varepsilon_{i}\)に対する\(n_{i}\)を求める。 \begin{align} \Psi &= k_{\text{B}}T\ln W - \alpha N - \beta E \nonumber \\ &= k_{\text{B}}T \sum_{i} W_{i} \ln W_{i} - \alpha \sum_{i} n_{i} - \beta \sum_{i} n_{i} \varepsilon_{i} \label{eq:Lagf} \end{align} ここで、\(n_{i}\)と\(\varepsilon_{i}\)に対する制約条件は、 それぞれ式\(\eqref{eq:Nb}\)と式\(\eqref{eq:Eb}\)と同じである。 \(\Psi=\sum_{i} \psi_{i}\)として、各\(\varepsilon_{i}\)に対して、 \(k_{\text{B}} T \ln W\)を最大にする\(n_{i}\)と、未定な乗数\(\alpha\)と\(\beta\)との関係は、 \begin{align*} \frac{\partial \psi_{i}}{\partial n_{i}} = k_{\text{B}}T \left( - \ln n_{i} + \ln (g_{i}-n_{i}) \right) -\alpha - \beta \varepsilon_{i} = 0 \end{align*} を満足する。この偏微分を行うにあたり、式\(\eqref{eq:Wf2}\)を用いると分かりやすい。 よって、 \begin{align} \frac{n_{i}}{g_{i}} = \frac{1}{\exp \left( \frac{\alpha + \beta \varepsilon_{i}}{k_{\text{B}}T} \right) + 1} \label{eq:Lagfi} \end{align} を得る。 \(n_{i}/g_{i}\)は、エネルギー準位\(\varepsilon_{i}\)を構成する\(g_{i}\)個の状態のなかで、 粒子を見いだす確率を表すので、 エネルギー準位に対する粒子に分布関数(粒子を見出す確率)である。 式\(\eqref{eq:Lagfi}\)中の\(\beta\)は、 式\(\eqref{eq:dS}\)と\(\eqref{eq:dPsi}\)の議論から同様に\(\beta=1\)である。 また、エネルギーの基準はどこにとっても構わないので、 \(\alpha = - \mu\)とする。 そして、離散的な\(\varepsilon_{i}\)を連続変数\(\varepsilon\)にして、分布関数として、 \begin{align} f(\varepsilon) = \frac{1}{\exp \left( \frac{\varepsilon - \mu}{k_{\text{B}}T} \right) + 1} \label{eq:Fermi} \end{align} を得る。 この式\(\eqref{eq:Fermi}\)がFermi-Dirac統計が与える分布関数であり、Fermi分布とも呼ばれる。 この分布関数に従うものは、電子のほかに陽子や中性子などがあり、 これらの粒子をFermi粒子またはFermionと呼ぶ。 特に、式\(\eqref{eq:Fermi}\)の\(\mu\)を、フェルミエネルギー\(\varepsilon_{F}\)にすると、 固体中の電子のエネルギーに対する分布関数(Fermi-Diracの分布関数)となる。
この統計が対象する粒子は、「個々の区別ができなく、 各\(\varepsilon_{i}\)の\(g_{i}\)個の状態にいくつでも入ることができる」性質がある。 このような粒子の集団において、 各粒子が各エネルギーの各状態に分配される場合の数を考える。 Fig.4のように\(\varepsilon_{i}\)の準位に\(g_{i}\)個の枡を一列に並べて、 その枡の中に数を気にせず\(n_{i}\)個の粒子を入れる入れ方が、 何通りあるかを考えれば良い。 もっと単純化すれば、対象の粒子を白い粒子、赤色で描いた枡の仕切りを赤い粒子に描き、 \(n_{i}\)個の白い粒子と\(g_{i}-1\)個の赤い粒子を、 1列に並べる場合の数を考えれば良い。 この順列は、 \begin{align*} (n_{i}+g_{i}-1)! \end{align*} 通りある。白い粒子は互いに区別がつかず、赤い粒子も互いに同等であるので、 上の順列を\(n_{i}!\)と\((g_{i}-1)!\)で割ったものが、 \(\varepsilon_{i}\)の\(g_{i}\)個の状態に\(n_{i}\)個の粒子を分配する場合の数\(W_{i}\)なので、Fig.4に示すように、 \begin{align*} W_{i} = \frac{(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!} \end{align*} となる。 従って、\(N\)個の粒子全てを、各エネルギー準位に分配する場合の数\(W\)は、 以下のようになる。 \begin{align} W = \prod_{i} W_{i} = \prod_{i} \frac{(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!} \label{eq:Wbe} \end{align}
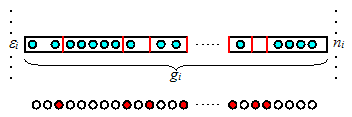 |
⇒ \(W_{i} = \frac{(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!}\) |
|
Fig.4: 個々の区別がなく、各エネルギー準位を構成する各状態に 幾つでも粒子を配置できる場合. |
|
式\(\eqref{eq:Wbe}\)の\(W\)を用いて、 \(k_{\text{B}}T \ln W\)を最大にする、 各\(\varepsilon_{i}\)に対する\(n_{i}\)の関係式を求める。 式\(\eqref{eq:Wbe}\)の両辺の対数を取り、スターリングの公式を用いてまとめると、 \begin{align} \ln W & = \sum_{i} \{ (n_{i}+g_{i}-1) \ln (n_{i}+g_{i}-1) - n_{i} \ln n_{i} - (g_{i}-1) \ln (g_{i}-1) \} \nonumber \\ & \approx \sum_{i} \{ (n_{i}+g_{i}) \ln (n_{i}+g_{i}) - n_{i} \ln n_{i} - (g_{i}-1) \ln (g_{i}-1) \} \label{eq:Wbe2} \end{align} を得る。 ただし、\(n_{i}+g_{i} \gg 1\)なので、 \(n_{i}+g_{i}-1 \approx n_{i}+g_{i}\)と近似した。 式\(\eqref{eq:Lagb}\)および式\(\eqref{eq:Lagf}\)と同様に、 \(\Psi\)を定義して、ラグランジュの未定乗数法により、 \(k_{\text{B}} T \ln W\)を最大にする\(\varepsilon_{i}\)に対する\(n_{i}\)を求める。 \begin{align} \Psi = k_{\text{B}}T \sum_{i} W_{i} \ln W_{i} - \alpha \sum_{i} n_{i} - \beta \sum_{i} n_{i} \varepsilon_{i} \label{eq:Lagbe} \end{align} ここで、\(n_{i}\)と\(\varepsilon_{i}\)に対する制約条件は、 それぞれ式\(\eqref{eq:Nb}\)と式\(\eqref{eq:Eb}\)と同じである。 \(\Psi=\sum_{i} \psi_{i}\)として、各\(\varepsilon_{i}\)に対して、 \(k_{\text{B}} T \ln W\)を最大にする\(n_{i}\)と、未定な乗数\(\alpha\)と\(\beta\)との関係は、 \begin{align*} \frac{\partial \psi_{i}}{\partial n_{i}} = k_{\text{B}}T \left( \ln (n_{i}+g_{i}) - \ln n_{i} \right) -\alpha - \beta \varepsilon_{i} = 0 \end{align*} を満足する。この偏微分を行うにあたり、式\(\eqref{eq:Wbe2}\)を用いた。 従って、 \begin{align} \frac{n_{i}}{g_{i}} = \frac{1}{\exp \left( \frac{\alpha + \beta \varepsilon_{i}}{k_{\text{B}}T} \right) - 1} \label{eq:Lagbei} \end{align} を得る。 \(n_{i}/g_{i}\)は、 エネルギー準位\(\varepsilon_{i}\)の状態数に対する粒子の割合(粒子を見出す確率)を表す。 式\(\eqref{eq:Lagbei}\)中の\(\beta\)は、 式\(\eqref{eq:dS}\)と\(\eqref{eq:dPsi}\)の議論から同様に\(\beta=1\)である。 また、エネルギーの基準はどこにとっても構わないので、 \(\alpha = - \mu\)とする。 そして、離散的な\(\varepsilon_{i}\)を連続変数\(\varepsilon\)にすると、分布関数として、 \begin{align} f(\varepsilon) = \frac{1}{\exp \left( \frac{\varepsilon - \mu}{k_{\text{B}}T} \right) -1} \label{eq:BE} \end{align} を得る。この式\(\eqref{eq:BE}\)がBose-Einstein統計が与える分布関数であり、Bose分布とも呼ばれる。 この分布関数に従うものは、フォトン(光子)やフォノン、超伝導体の電流を担うクーパー対などがあり、 これらの粒子をBose粒子またはBosonと呼ぶ。
古典論に従う粒子の集団はMaxwell-Boltzmann統計に従い、 量子論に従う粒子の集団は、Fermi-Dirac統計またはBose-Einstein統計に従う。 そして、Maxwell-Boltzmann統計、Fermi-Dirac統計、Bose-Einstein統計が与える分布関数は、 それぞれ式\(\eqref{eq:Boltz}\)、式\(\eqref{eq:Fermi}\)、式\(\eqref{eq:BE}\)である。 これらの分布関数をFig.5に比較した。 グラフの横軸は\((\varepsilon - \mu)/k_{\text{B}}T\)であることに注意してほしい。
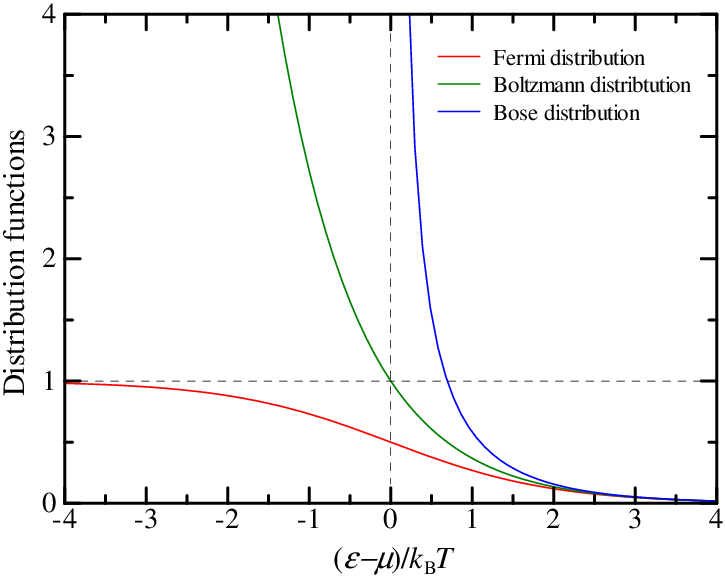 |
| Fig.5: 分布関数の比較. |
\((\varepsilon - \mu)/k_{\text{B}}T \gg 1\)で、3つの分布関数の区別がつかなくなる。 量子論の基づくFermi分布とBose分布が、古典論に基づくBoltzmann分布に近づくという意味で、 「古典領域」と言う。 Fermi分布では、\((\varepsilon - \mu)/k_{\text{B}}T \ll 0\)で1に漸近する。 Bose分布では、\((\varepsilon - \mu)/k_{\text{B}}T = 0\)で発散する。 このことから、Boltzmann分布を基準に比較すると、 Bose-Einstein統計に従う粒子の集団は互いに同じ状態に集まろうとする傾向があり、 Fermi-Dirac統計に従う粒子の集団はその反対の傾向にあると言えよう。
|
Last Updated: |