⇒直線偏光
偏光面の向き
円偏光二色性(CD)スペクトルを測定すると、楕円率やモル楕円率なる量が出てくる。
円偏光二色性は、左右の円偏光の吸光係数の差、あるは吸光度の差として教わるが、
それがなぜ楕円率と関係するのか、疑問をもつであろう。
その疑問に答えるため、簡単な旋光性から解説し、円偏光二色性における左右の円偏光の吸光係数の差と、楕円率の関係について解説した。
なお、この解説の作成にあたり、以下の文献を参考にした。
爪谷郁三,志村憲助,中村道徳,船津勝=編集,生物化学実験法6
浜口浩三,武貞啓子 著 蛋白質の旋光性 〈ORDとCD〉,学会出版センター,ISBN:4-7622-0107-3
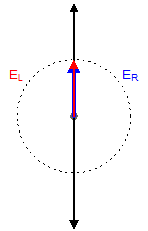
旋光性とは、直線偏光の偏光面を回転させる性質である。 その原因は、右回り円偏光と左回り円偏光に対する屈折率が、 異なること(\(n_{\text{R}} \neq n_{\text{L}}\))にある。 Fig.1(a)と(b)に、 振幅が等しい左右の円偏光の電気ベクトル(\(E_{\text{R}}, E_{\text{L}}\))の回転の仕方を示した。 ここで、光波の進む方向は、現在見ているモニターから、モニターを見ている者へ向う。 Fig.1(a)と(b)の両円偏光の電気ベクトルは、ある時刻で同時に上、または下に向く。 ここでは、この状態を位相の基準状態とし、両円偏光の位相差が無い(\(\phi = 0\))状態とする。 この両円偏光を重ね合わせると、 Fig.1(c)のように電気ベクトルを上下に振動させる直線偏光となる。
 |
|||
| (a)右回り円偏光 | (b)左回り円偏光 | (c)左右円偏光の合成 ⇒直線偏光 |
(d)直線偏光の 偏光面の向き |
Fig.1 円偏光の種類と重ね合わせ.
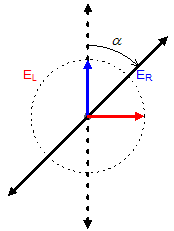
Fig.1(a)と(b)の円偏光が、 それぞれに対する屈折率が異なる媒質(\(n_{\text{R}} < n_{\text{L}}\))を通過したら、 右回り円偏光に対して、 左回り円偏光の位相がFig.1(b)の状態から\(\phi = \frac{\pi}{2}\)[rad]遅れたとする。 その状態をFig.2(b)に示した。 この状態で、Fig,2(a)と(b)の両円偏光を合成すると、Fig.2(c)のような直線偏光になるが、その偏光面は、 Fig.1(c)の偏光面と比べると、 \(\frac{\phi}{2} = \frac{\pi}{4}\)[rad]時計回りに傾く。 これが、直線偏光の偏光面を回転させる旋光性である。
 |
|||
| (a)右回り円偏光 | (b)左回り円偏光 | (c)左右円偏光の合成 ⇒直線偏光 |
(d)直線偏光の 偏光面の向き |
Fig.2 左回り円偏光の位相が,Fig.1(b)の状態から\(\frac{\pi}{2}\)[rad]遅れた場合の重ね合わせ.
一般的には、両円偏光の位相差が\(\phi\)の場合、 両円偏光の合成である直線偏光の偏光面は、 角度\(\alpha = \frac{\phi}{2}\)だけ回転することになる。 従って一般的な場合ついて書くと、波長\(\lambda\)の両円偏光が、 長さ\(l\)の試料を進むと、両円偏光の間に生じる位相差\(\phi\)は、 式\(\eqref{eq:phi}\)で与えられる。また、試料通過前後で、直線偏光の偏光の回転角は、 式\(\eqref{eq:alpha}\)で与えられる。 \begin{align} \phi=2\pi l (\frac{n_{\text{L}}}{\lambda}-\frac{n_{\text{R}}}{\lambda})=\frac{2\pi l}{\lambda}(n_{\text{L}}-n_{\text{R}}) \label{eq:phi} \end{align} \begin{align} \alpha=\frac{\pi l}{\lambda}(n_{\text{L}}-n_{\text{R}}) \label{eq:alpha} \end{align}
左右の円偏光に対する屈折率\(n_{\text{L}}\)と\(n_{\text{R}}\)が異なるときには、
往々にして左右の円偏光に対する吸収係数\(\varepsilon_{\text{L}}\)と\(\varepsilon_{\text{R}}\)も異なる。
\(\varepsilon_{\text{L}}\)と\(\varepsilon_{\text{R}}\)が異なる現象を円偏光二色性という。
従って、基本的には旋光性と円偏光二色性は同時に起こることとなり、
このような媒質をFig.1(c)のような直線偏光が通過すると、
左右の円偏光の位相差が生じると同時に、
光電界の大きさ\(E_{\text{L}}\)と\(E_{\text{R}}\)も異なる。
この2つの効果が同時に起こる現象をCotton効果という。
そこで、直線偏光が旋光性と円偏光二色性がある媒質を通過後、
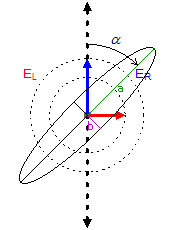
その偏光状態がどのように変化するのかをFig.3に示した。
Fig.3(b)のように、右回り円偏光に対して、
左回り円偏光の位相がFig.1(b)の状態から\(\phi = \frac{\pi}{2}\)[rad]遅れ、
かつ左回り円偏光の光電界の大きさが、
右回り円偏光のそれより小さくなった(\(E_{\text{L}} < E_{\text{R}}\))とする。
Fig.3(a)の右回り円偏光とFig.3(b)の左回り円偏光を合成すると、
Fig.3(c)に示すように楕円偏光となる。
吸収係数の違いを考慮しなかったFig.2(d)と、
その違いを考慮したFig.3(d)の偏光状態を比較すると、
左右の円偏光の位相差が同じであれば、
Fig.2(d)の偏光面の回転角\(\alpha\)は、
Fig.3(d)の楕円の主軸(長軸)の傾き角\(\alpha\)と等しい。
そして、吸収係数の違いは、
直線偏光が楕円偏光に変えられることに反映される。
従って、透過後の楕円偏光の状態と円偏光二色性には、
深い関係があることが想像できる。
 |
|||
| (a)右回り円偏光 | (b)左回り円偏光 | (c)左右円偏光の合成 ⇒楕円偏光 |
(d)楕円偏光の長軸と短軸の 長さと方向 |
Fig.3 左回り円偏光の位相が,Fig.1(b)の状態から\(\frac{\pi}{2}\)[rad]遅れ、
かつ左回り円偏光の光電界の大きさに差が生じた場合の重ね合わせ.
そもそも、「左右の円偏光に対する吸収係数の差」が円偏光二色性であるから、
それぞれのモル吸光係数を\(\varepsilon_{\text{L}}, \varepsilon_{\text{R}}\)と
おくと、円偏光二色性は式\(\eqref{eq:delep}\)で定義される。
\begin{align}
{\it \Delta}\varepsilon=\varepsilon_{\text{L}} - \varepsilon_{\text{R}}
\label{eq:delep}
\end{align}
厚さが\(l\)で、濃度\(c\)の試料の場合、左右の円偏光の吸光度を\(A_{\text{L}}, A_{\text{R}}\)とすると、その差、
\begin{align}
(A_{\text{L}} - A_{\text{R}}) & = (\varepsilon_{\text{L}} - \varepsilon_{\text{R}}) \cdot c \cdot l \\
{\it \Delta}A & = {\it \Delta}\varepsilon \cdot c \cdot l
\label{eq:delabs} \\
\end{align}
である。濃度\(c\)の単位を[mol/L]=[mol/dm3]、
セル厚\(l\)の単位を[cm]としたとき、\({\it \Delta}\varepsilon\)を「モル円偏光二色性(モル円二色性)」と呼ぶ。素直に考えれば、
円偏光二色性スペクトルは、式\(\eqref{eq:delabs}\)のスペクトルと想像する。
しかし、円偏光二色性スペクトルを見ると、
その縦軸は「楕円率(Ellipticity)」とある。
この楕円率とは、Fig.3(d)の楕円偏光の楕円率で、
短軸\(b\)と長軸\(a\)の比から定義される角度\(\delta\)[rad]のことであり、
\begin{align}
\tan \delta = \frac{b}{a}
\label{eq:del}
\end{align}
で与えられる。そもそも楕円率とは、楕円体の短軸と長軸の比\(b/a\)なのだが、
円偏光二色性の場合には、
式\(\eqref{eq:del}\)の角度\(\delta\)[rad]のことを「楕円率(Ellipticity)」と呼ぶ。
この楕円率\(\delta\)[rad]は、
円偏光二色性の定義である式\(\eqref{eq:delep}\)の\({\it \Delta}\varepsilon\)と関係しているのである。
以下に両者の関係性について解説する。
試料を透過後、生成される楕円偏光は、非常に細長く、
ほぼ直線偏光とみなせるとすると、
\begin{align}
\delta \approx \frac{b}{a}
\label{eq:del2}
\end{align}
と近似できる。
一方、ランバート・ベールの法則から、左右の円偏光の強度が\(I_{0}\)に等しい場合、それぞれの円偏光の透過後の強度は、
\begin{align}
& I_{\text{L}} = I_{0} \times 10^{-\varepsilon_{\text{L}} \cdot c \cdot l} &
& I_{\text{R}} = I_{0} \times 10^{-\varepsilon_{\text{R}} \cdot c \cdot l} &
\label{eq:I}
\end{align}
と表せる。
従って、それぞれの光電界の大きさは、
\begin{align}
& E_{\text{L}} \propto 10^{-\frac{1}{2}\varepsilon_{\text{L}} \cdot c \cdot l} &
& E_{\text{R}} \propto 10^{-\frac{1}{2}\varepsilon_{\text{R}} \cdot c \cdot l} &
\label{eq:E}
\end{align}
と表される。入射強度が等しいとしているので、
式\(\eqref{eq:E}\)の比例係数はそれぞれ等しい。
Fig.3(c)と(b)を見れば分かるように、
透過後の楕円偏光の楕円体の短軸\(b\)と長軸\(a\)の比は、
左右の円偏光の光電界の大きさ\(E_{\text{L}}\)と\(E_{\text{R}}\)を用いて、
\begin{align}
\frac{b}{a} = \frac{E_{\text{R}}-E_{\text{L}}}{E_{\text{R}}+E_{\text{L}}}
\label{eq:b/a}
\end{align}
と表される。式\(\eqref{eq:b/a}\)に式\(\eqref{eq:E}\)を代入してまとめると、
\begin{align}
\frac{E_{\text{R}}-E_{\text{L}}}{E_{\text{R}}+E_{\text{L}}}
& =
\frac{
10^{-\frac{1}{2}\varepsilon_{\text{R}} \cdot c \cdot l}-10^{-\frac{1}{2}\varepsilon_{\text{L}} \cdot c \cdot l}
}{
10^{-\frac{1}{2}\varepsilon_{\text{R}} \cdot c \cdot l}+10^{-\frac{1}{2}\varepsilon_{\text{L}} \cdot c \cdot l}
} \\
& =
\frac{1}{
1+10^{-\frac{1}{2}(\varepsilon_{\text{L}}-\varepsilon_{\text{R}}) \cdot c \cdot l}
} -
\frac{1}{
1+10^{\frac{1}{2}(\varepsilon_{\text{L}}-\varepsilon_{\text{R}}) \cdot c \cdot l}
} \\
& =
\frac{
10^{\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}-
10^{-\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}
}
{
2+
10^{\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}+
10^{-\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}
}
\label{eq:b/a2}\\
\end{align}
のようになる。
前提として、「試料を透過後、生成される楕円偏光は、非常に細長く、
ほぼ直線偏光とみなせる」としているので、
左右の円偏光の吸光係数の差は非常に小さい。
従って、\({\it \Delta}\varepsilon \ll 1\)として、式\(\eqref{eq:approx}\)に示す近似を行う。
\begin{align}
& 10^{\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l} \approx
1 + (\log_{e} 10^{\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon &
& 10^{-\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l} \approx
1 + (\log_{e} 10^{-\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon &
\label{eq:approx}
\end{align}
式\(\eqref{eq:approx}\)を式\(\eqref{eq:b/a2}\)に代入すると、
\begin{align}
\frac{E_{\text{R}}-E_{\text{L}}}{E_{\text{R}}+E_{\text{L}}}
& =
\frac{
10^{\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}-
10^{-\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}
}
{
2+
10^{\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}+
10^{-\frac{1}{2} {\it \Delta}\varepsilon \cdot c \cdot l}
} \\
& \approx
\frac{
(\log_{e} 10^{\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon -
(\log_{e} 10^{-\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon
}
{
4+
(\log_{e} 10^{\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon +
(\log_{e} 10^{-\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon
} \\
& =
\frac{1}{2}(\log_{e} 10^{\frac{1}{2}c \cdot l}) {\it \Delta}\varepsilon
\label{eq:b/a3}
\\
\end{align}
となる。最後に対数の底の変換を行って、
\(\log_{e} 10^{\frac{1}{2}c \cdot l} = \frac{1}{2}c \cdot l / \log_{10}e\)としてやると、式\(\eqref{eq:del2}\)と式\(\eqref{eq:b/a}\)と式\(\eqref{eq:b/a3}\)より、
円偏光二色性の楕円率\(\delta\)[rad]は、
\begin{align}
\delta & \approx \frac{1}{4\log_{10}e} {\it \Delta}\varepsilon \cdot c \cdot l~\text{[rad]} \\
& = \frac{180}{4\pi\log_{10}e} {\it \Delta}\varepsilon \cdot c \cdot l~\text{[deg]} \label{eq:Ellip} \\
\end{align}
と表せる。結局、楕円率\(\delta\)は、
左右の円偏光の吸光係数の差\({\it \Delta}\varepsilon=\varepsilon_{\text{L}} - \varepsilon_{\text{R}}\)と比例関係にある。
これが、円偏光二色性スペクトルの縦軸が、
「楕円率(Ellipticity)」となる所以である。
式\(\eqref{eq:Ellip}\)から、濃度\(c\)[10mol/L]、
厚さ\(l\)[dm]としたときの\(\delta / c \cdot l~\)を\([\theta]\)と表記して、
「モル楕円率」と呼ぶ。
その単位は[deg・cm2/dmol]である。
モル円偏光二色性\({\it \Delta}\varepsilon\)の単位は、
[dm3/cm・mol]である。
\begin{align}
1~\biggl[ \frac{\text{dm}^{3}}{\text{cm} \cdot \text{mol}} \biggr] =
100~\biggl[ \frac{\text{cm}^{2}}{\text{dmol}} \biggr]
\label{eq:unit}
\end{align}
なる関係がある。式\(\eqref{eq:Ellip}\)と式\(\eqref{eq:unit}\)より、モル楕円率\([\theta]\)と、モル円偏光二色性\({\it \Delta}\varepsilon\)の間に、
\begin{align}
[\theta] = 100 \times \frac{180}{4\pi\log_{10}e} {\it \Delta}\varepsilon =
3298 {\it \Delta}\varepsilon
\label{eq:molellip}
\end{align}
なる関係がある。
|
Last Updated: |