第5回　表計算ソフトによるデータ処理(2)

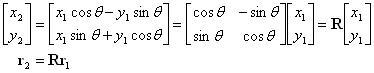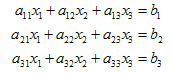
前回は表計算ソフトの基本的な利用法を学んだ。今回は、それを一歩進めて、様々な工学分野で必要になる、多元の連立方程式の行列による表し方、表計算ソフトでの作成法、及びその解法を学ぶ。またこのことを通じて行列演算の有用性を体感し、データ処理の技術を身につける。

本講義で身につけた知識が役立つ科目等：
　実験工学・演習、FEM解析、機械力学I, II、コンピュータ機械工学、機械工学実験、
　機械設計製図２、メカトロニクス実習、ゼミナール、卒業研究など

5.1 連立方程式と行列

機械工学の様々な分野で、以下の様な連立方程式の解を得ることが要求される。

　　

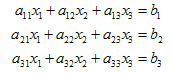
が成立つとすると、未知変数はである。数値的に解を得るため行列表記とすると、

　　

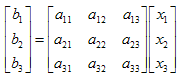
となる。これは即ち、

　　

である。ここで係数行列Aの逆行列A-1を用いれば、以下のように解xが得られる。

　　

　　

5.2 Excelによる行列演算

では具体的にExcelを用いて行列演算をしてみよう。具体的な例として、

　　

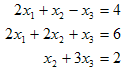
を考える。これを行列表記にすると

　　

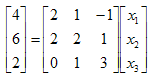
となる。まずはこれを以下のようにExcelで表現してみよう。

　　

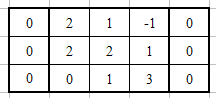
右辺の係数行列とxには数値を入れ、左辺には行列とベクトルの乗算を行う計算式を入力する。

1。計算式を手入力する場合

計算式を入力する左上のセル番地がA1であるとき、ここに入力されるべき計算式は、

=B1*E1+C1*E2+D1*E3

である。A2とA3にも同様に式を入力する。

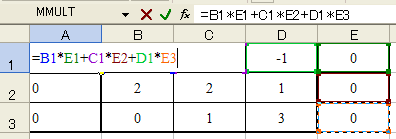
これで、行列Aとベクトルxの乗算が完成した。右のに様々な数値を入力して、計算が正しく行われているかどうかを確認せよ。

Tips(Offece2007): 式が正しく入力できたかどうかを確認するには、「数式」タブの「ワークシート分析」欄にある、「数式の表示」を押すと、計算結果の代わりに数式が表示される。

2。Excel組込の行列演算関数を利用する場合

セルA1には以下の行列関数を入力する。

=MMULT(B1:D3,E1:E3)

ここで、MMULT()は行列と行列、または行列とベクトルの乗算を行う関数であり、第1引数は、左側、第2引数は右側の行列あるいはベクトルを示している。MMULT()はまた、配列数式*を返します。従って、セルA1にのみMMULT()を入力しても正しく機能せず、A2とA3にも配列数式を入力する必要がある。この例の場合、A1:A3を選択してからF2キーを押し、その後、Ctrl+Shift+Enterを入力する。

Tips: 関数の入力が終わったら、関数が入るべき範囲を選択してからF2を押し、Ctrl+Shift+Enterを入力する。

計算式を手入力した場合と結果が同じになるかどうか確認してみよ。

*配列数式：Excelのヘルプを参照の事

5.3 逆行列の演算

では次に、逆行列を作ってみよう。行列式

　　

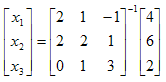
をExcel上で以下のように作成する。わかりやすくするために、先に作った行列(B1:D3)は残し、その下（以下の例ではB5:D7の部分）に逆行列を作成してみる。

B5への入力が終わったら、MMULT()の時と同様に、B5:B7を選択してからF2を押し、その後、Ctrl+Shift+Enterを入力する。すると、逆行列が以下のように求まる。

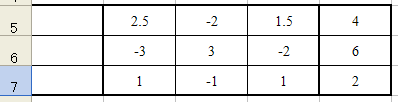
逆行列を求める為には、正方行列で無くてはならないことに注意せよ。
行列に依っては逆行列が計算不可である場合もある。

最後に、MMULT()を用いて行列とベクトルの乗算を行えば、xを求めることができる。

得られた解は何か？　得られた解を、初めの順計算の式b=Axに代入して、同じbが得られるかどうか、確認してみよ。

5.4 その他の行列演算関数

その他のExcel組込の行列演算関数には、転置TRANSPOSE()がある。

課題

以下の計算を1つのExcelワークシート上に作成し、作成したExcelファイルを提出せよ。提出期限は来週正午までとする。

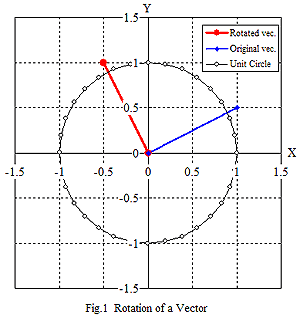    VectorRotation
    位置ベクトルの回転（図中の座標は一例）
  1. 2次元座標上の点r1=(x1,y1)を、原点を中心に角度θ回転させる式は、以下で与えられる。

    　

    この式を利用して、r1=(x1,y1)およびθが与えられた際にr2を計算する表をExcelで作成せよ。
    様々なx1,y1およびθを与えて、計算が正しく行われていることを確認すること。

  2. x軸上の点(1.5, 0)を、角度45度 および 90度回転させると、回転後の座標はそれぞれどのようにになるか？　1.で作った表を使って計算し、ワークシート中に回答せよ。

  3. 逆行列の演算を利用し、r2を入力するとr1が得られる表を 1.の表の下方に作成せよ。 なおこの計算は、角度-θの回転に相当することになる。

  4. 1. で作成した行列Rの転置行列RTを計算し、3の逆行列の計算結果と同一になることを確認せよ。 3.の表の下方に転置行列を作成すること。