Webページでは数式を表すためにLaTeX表記が使えるMathJaxを利用しています。
WebブラウザにはSafari/Chrome/Firefoxを使って下さい（IEでは表示できないようです。）
Lorenz系の解析
承前
微分方程式の数値解法- Euler法とRunge-Kutta法
数値解の誤差- 精度保証の問題、W. Tucker(2002)の研究
初期条件を与えればそれ以降の挙動は決定論的に（解の存在と一意性があれば）一意的に定まってしまう微分方程式（力学系ともいう）の研究において、 Edward N. LorenzのDeterministic Nonperiodic Flow J. Atmos. Sci., 20(11963), 130–141)は極めて大きな役割を果たした。 ほんの僅かな初期条件の違いによって、その後の挙動が極めて鋭敏に依存して全く異なってしまうという初期条件鋭敏性（sensitive dependence on initial conditions）によって、決定論的仕組みにもかからわず、事実上挙動が予想できないというカオス（chaos）研究の先鞭をつけた。
Lorenz系をRで数値計算でも取り上げたが、数値軌道を調べてみよう。 ベクトル場のパラメータは以降 $p = 10.0$ , $r = 28.0$, $\displaystyle b = \frac{8}{3}$ とする。 パラメータ依存性の研究では、$p=10, b=8/3$ を固定して、$r$ を変化させるのが通例である。
Poincareの切断面の方法 surface of section
この$1 < r$のとき、ベクトル場には原点 $(0,0,0)$ 以外に2つの不動点 $C_{\pm}$ \[ C_{\pm}=(\pm\sqrt{b(r-1)}, \pm\sqrt{b(r-1)}, r-1) \] が現れることが分かっている（z成分は2点とも同じ高さ$r - 1$にある）。 真の軌道$(x(t), y(t), z(t))$ は平面 $z=r-1$ で定まる$xy$-平面 $\Sigma_{z=r-1}$ を「下から上に」あるいは「上から下へ」と横断（transverse）する。 たとえば、「下から上に」平面 $\Sigma_{z=r-1}$ を横断する$xy$-座標を求めてみよう。
Lorenz系の3つの軌道要素 $\boldsymbol{x}=(x,y,z)$ を持つ数値軌道リスト [$\boldsymbol{x}_0$, $\boldsymbol{x}_1$, $\dots$, $\boldsymbol{x}_N$] において、各要素の$z$-成分の列 $[z_0,z_1,\dots, z_N]$ に注目する。 各$z$要素から平面 $\Sigma_{z=r-1}$ の高さを引いたリスト \begin{align*} & [z_0-(r-1),z_1-(r-1),\dots, z_N-(r-1)]\\ =& [s_0,s_1,\dots,s_N],\qquad s_j=z_j-(r-1) \end{align*} を考える。
$k$番目の点 $\boldsymbol{x}_k$ が平面 $\Sigma_{z=r-1}$ を「下から上に」横断するとは、$k+1$番目の点 $z_{k+1}$ が次のように続いているときである：
\[ \text{$z_k-(r-1) < 0$ and $z_{k+1}-(r-1)<0$} \Leftrightarrow \text{$s_k > 0$ and $s_k s_{k+1}<0$} \]ベクトル場が滑らかで時間刻みが十分に小さければ、そのような$z$-成分を持つ点 $\boldsymbol{x}_k$ は平面 $\Sigma_{z=r-1}$ にごく近いと見なすことができる。 こうした$z$-成分を持つ点 $\boldsymbol{x}_k$について $(x,y)$は軌道横断する平面 $\Sigma_{z=r-1}$ における交点 $P$ であるとみなす。
Lorenz系の軌道を観察してみると、軌道は2つの不動点 $C_\pm$の周りを回り続けており、平面 $\Sigma_{z=r-1}$ を何度でも横断していることがわかる。
周期軌道に点 $\boldsymbol{x}^*$で横断的な平面 $\Sigma$ を考える。 平面 $\Sigma$ 上にある点 $\boldsymbol{x}^*$の十分近くから出発した軌道は再び $\Sigma$ を同じ方向に横切る。 このとき、微分方程式が定める流れは平面 $\Sigma$ から $\Sigma$ への写像 \[ P: \Sigma \rightarrow \Sigma \] を定めているという。 周期軌道と$\Sigma$との交点 $\boldsymbol{x}^*$は写像$P$の不動点$P(\boldsymbol{x}^*)=\boldsymbol{x}^*$である。 周期軌道に近傍で定義される平面 $\Sigma$ 上の写像をPoincare写像という。
こうして、$n$次元の微分方程式の研究は、周期軌道が存在するとき、それに横断的に横切る $n-1$ 次元横断面 $\Sigma$ 上のPoincare写像の研究に帰着される。
# -*- coding: utf-8 -*-
# numerila solution fo Lorenz system using scipy.integrate
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# lorenz system
p, r, b = 10.0, 28.0, 8.0 / 3.0
def lorenz_system(x, t):
vxt = -p * x[0] + p * x[1]
vyt = -x[0] * x[2] + r * x[0] - x[1]
vzt = x[0] * x[1] - b * x[2]
return([vxt, vyt, vzt])
x0 = [0.1, 0.1, 0.1]# initial points
t0 = 0
T = 100
dt = 0.01
# numerila solution using scipy.integrate
times = np.arange(t0, T, dt)
orbit = odeint(lorenz_system, x0, times)
# Poincare surface of section
# z = r-1 のx-y平面を増加して横切るときの(x,y) をplot
xsectionlist = []
ysectionlist = []
zhight = [0, 0, r-1]
# points transversing the plane upword
for k in range(len(orbit)-1):
if (orbit[k] - zhight)[2] < 0 and (orbit[k] - zhight)[2] * (orbit[k+1] - zhight)[2] < 0:
xsectionlist.append(orbit[k,0])
ysectionlist.append(orbit[k,1])
#plot using matplotlib
ax = plt.axes()
plt.xlabel('x')
plt.ylabel('y')
plt.plot(xsectionlist, ysectionlist, "x", markersize=1)
plt.show()
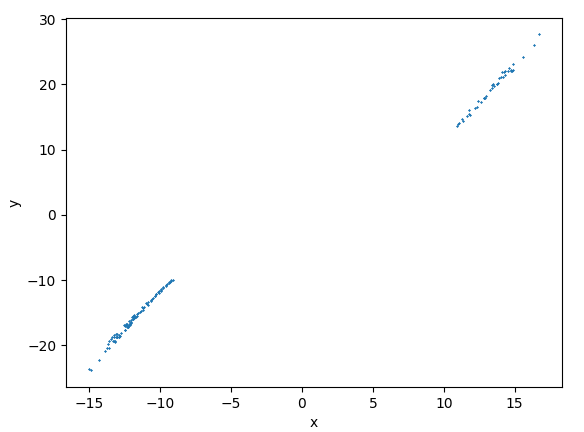p=10, r=28.0, b = 8.0/3.0のとき、SciPyの数値積分法によるLorenz系の軌道の Z= r-1 のxy平面での下から上への軌道横断のプロット。
初期条件 (0.1,0.1,0.1), 時間刻み dt = 0.01, 時間 T = 100.
Lorenzプロット
Lorenzの大発見に導いた本質的な方法である。 E. N. LorenzはDeterministic Nonperiodic Flow J. Atmos. Sci., 20(11963), 130–141)において、今日ではLorenzプロットとして知られる力学系の対象次元をさらに減らす別の方法を提案した（論文のFig(4)）。
原点近くを出発した軌道は、今のパラメータの設定値では、双曲不安定点である原点を離れてしばらくすると（移行期を過ぎると）、二つの$z=r-1$の高さにある2つの不動点 $C_{\pm}$ の回りを不規則的に交互に周回する。 不動点 $C_+$の周りを何回か周回して不動点 $C_-$ の周りに移り、$C_-$の周りを何回転かしてから再び$C_+$の周りに移り、を交互に不規則に繰り返し続けるのである。
軌道 $\boldsymbol{x}(t)=(x_1(t), x_2(t), \dots, x_n(t)$ が有限領域に留まって動いているとしよう。 今、ある座標成分$x_i$-成分$x_i(t)$の変化に着目すると、ある時刻$t_k$があって、時刻$t_k$をはさむ近傍時間 $t\in (t_k-\varepsilon, t_k+\varepsilon)$ で $x(t) < x (t_k)$となるような時系列 $\{t_i\}$, つまり、$x_i(t)$が時刻$t_k$ごとに局所的に極大値$x^*_k$となる系列 \[ x^*_1,x^*_2,\dots,x^*_k,\dots \] を考えることができる。 このとき、平面上に$(x^*_1,x^*_2), (x^*_2,x^*_3),\dots, (x^*_{k-1},x^*_k),(x^*_k,x^*_{k+1}), \dots)$をプロットして得られる様子をLorenzプロットという。
Lorenzは、3つの軌道要素 $\boldsymbol{x}=(x,y,z)$ を持つ軌道リスト [$\boldsymbol{x}_0$, $\boldsymbol{x}_1$, $\dots$, $\boldsymbol{x}_N$] において、$z$-成分の局所極大値列に注目した。 $z$ 成分の列 $(z_0,z_1,\dots, z_N)$ の隣り合う値の差 $dz_i = z_{i+1}-z_i$の列 \[ z_1-z_0, z_2-z_1, \dots, z_{i+1}-z_i,\dots \]において、 \[ \text{$z_{i-1}< z_i$ and $z_i > z_{i+1}$} \] となる$z_i$値を局所極大値$z^{max}_i$とし、その極大値列を求めその極大値列を求め、そのLorenzプロットを取った:
初期条件からの移行期までのステップ数を、たとえば transit = 500 として、transit番目以降の $z_i$ について、極大値列 zmaxlist \[ zmaxlist =[z^{max}_0,z^{max}_1,\dots,z^{max}_{i-1},z^{max}_i, z^{max}_{i+1},\dots,z^{max}_N] \] を求めるのである。
次のプログラム lorenz_plot.py は SciPyを使ってLorenz系を数値計算し、22-23行目で得られた軌道要素 orbit をndarray形式で求め、26-34行目でzmaxlistを求めている（局所極大となった時刻列maxtimeも）。 コメントアウトしている41-45行でmatplotlibに渡すリストzlistとnzlistを作成してもよいが、ここでは隣り合う組のプロットであることから36-38行目で作成した。
リストのコピーでは参照コピー（浅いコピー）されてしまうので、ここでは6行目でモジュール copyをインポートしてzmaxlistを copy.deepcopy(zmaxlist) によってメモリのベルの場所に深いコピーしている。こうして同じ内容のデータ zmaxlist とzlistは違うメモリ場所に存在している。
zlistとして np.delete(zlist, len(zmaxlist)-1) でリスト末尾を削除したリストとし、zmaxlistの先頭を np.delete(zmaxlist, 0) で削除して nzlist とした。 いずれも dnarray クラスであるために、Numpy方式を使っていることに注意する。
# -*- coding: utf-8 -*-
# numerila solution fo Lorenz system using scipy.integrate
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import copy
# lorenz system
p, r, b = 10.0, 28.0, 8.0 / 3.0
def lorenz_system(x, t):
vxt = -p * x[0] + p * x[1]
vyt = -x[0] * x[2] + r * x[0] - x[1]
vzt = x[0] * x[1] - b * x[2]
return([vxt, vyt, vzt])
x0 = [0.1, 0.1, 0.1]# initial points
t0 = 0
T = 100
dt = 0.01
# numerila solution using scipy.integrate
times = np.arange(t0, T, dt)
orbit = odeint(lorenz_system, x0, times)
# z-成分に関する局所極大値 z_max とそのときの時刻 t_max
zmaxlist = []
maxtime = []
transitstep = 500
for k in range(transitstep, len(orbit)-1):
dz0 = orbit[k,2] - orbit[k-1, 2]
dz1 = orbit[k+1,2] - orbit[k, 2]
if 0 < dz0 and dz1 < 0:
zmaxlist.append(orbit[k,2])
maxtime.append(dt * k)
zlist = copy.deepcopy(zmaxlist)
zlist = np.delete(zlist, len(zmaxlist)-1)
nzlist = np.delete(zmaxlist, 0)
# Lorenz plot {(z_i, z_i+1)} by means of zmaxlist
#zlist = []
#nzlist = []
#for j in range(len(zmaxlist)-1):
# zlist.append(zmaxlist[j])
# nzlist.append(zmaxlist[j+1])
#plot using matplotlib
ax = plt.axes().set_aspect('equal', 'datalim')
#plt.plot(times, orbit[:,2], "x", markersize=1)
plt.plot(zlist, nzlist, "x", markersize=1)
plt.xlabel('z(i)')
plt.ylabel('z(i+1)')
plt.show()
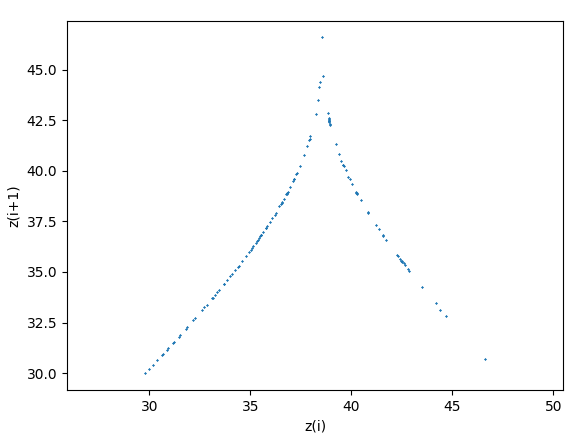
左図が有名なLorenzプロット の結果である（論文のFig(4)）。 この様子は、『次の』$z$-成分の局所極大値を与える1次元区間 $I$ から $I$自身への写像 $L$
\[ L:I \rightarrow I \] が存在することを強く示唆する。 もし、このテント型写像$L$が存在するならば、 $z_0\in I$ から$z_{n+1}=Lz_n=L^n z_0$ のように$L$を反復適用して得られる点列 $z_0,z_1,z_2,\dots$ として、Lorenz方程式の$z$方向の局所極大値が得られることになる（区間上の傾きの絶対値が1より大きいことが本質的で、このとき各点は区間上であかたもランダムに写像される）。 この写像の存在が明らかになれば、Lorenz方程式の研究は1次元区間 $I$ 上の写像 $L$ の研究に帰着されることになる。