グラフ理論 in Mathematica

数式処理システムを使ってグラフ理論を学ぶ

数式処理システムを使ってグラフ理論を学ぶ好著が既にある。 graphbookから入手できるPDFファイルAlgorithmic graph theory and Sageはオープンソースの数式処理システムSage（Win/Mac/Linux用のバイナリが提供されている）を使いながら、勉強できるたいへん興味深いテキストである（おそらく、Sageの入力を結果を直接LaTeXに取り込むSageTeXを使っているはずで、これまたLaTeXと数式処理システムの接近として面白い）。

MathematicaのGraphPlot/GraphPlot3D 関数は、特別なパッケージを読み込む必要もなく、隣接リスト情報を与えてそのグラフを描画することがでる（有用である）が、ただ描くだけで離散構造を取り出して操作することはできない（ドキュメントセンターグラフ描画）。 グラフを含む離散構造を数学的に取り扱うには Combinatorica パッケージ を使う。 組合せ論とグラフ理論に関する関数を集めたもので、ドキュメントセンターにあるチュートリアル Combinatorica が役にたつ。 Combinatorica パッケージは、以前のパッケージ DiscreteMath`Combinatorica` で実装され、テキスト 「Mathematica組み合わせ論とグラフ理論―離散数学を実現する」S. スキエナ（トッパン 1992）、Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica, S. Skiena, S.Pemmaraju（Cambridge University Press 2003)で解説されていた機能を拡張したものである。

Combinatorica パッケージ を読み込むには、Mathematica 内で次のように書く。 

<< Combinatorica`

ここで、記号 (`) はバッククォート(backquote)で「左上から右下に向かった」引用符である。 日本語キーボードでは [shift]+@ で入力することが多い。

代表的な組み込みグラフと描画

Combinatorica パッケージでは、代表的グラフ構造を呼び出して、さらにそれらを操作することができる。 完全グラフ $K_n$ は CompleteGraph[n] で、完全二部グラフ CompleteGraph[k, j] 次数 $n$ の星グラフは Star[n] で構築される。 また、頂点 $n$ のランダムツリー は RandomTree[n] で、辺の確率が $p$ で頂点$n$のランダムグラフ RandomGraph[n,p] で構築される。

グラフ g が構成されると、そのグラフの隣接行列は ToAdjacencyMatrix[g] で、隣接リストは ToAdjacencyMatrix[g] で与えられる。 

ToAdjacencyMatrix[CompleteGraph[5]] // MatrixForm
	0  1  1  1  1
	1  0  1  1  1
	1  1  0  1  1
	1  1  1  0  1
	1  1  1  1  0
ToAdjacencyLists[CompleteGraph[5]]
	{{2, 3, 4, 5}, {1, 3, 4, 5}, {1, 2, 4, 5}, {1, 2, 3, 5}, {1, 2, 3, 4}}

頂点 $1,2,\dots, N$ を持つグラフにおける頂点 $i$ が接続している頂点リスト $i\rightarrow \{v_{i_1},\dots,v_{i_k}\}$ は、ToAdjacencyLists によって $\ell_i=\{v_{i_1},\dots,v_{i_k}\}$ で表され、全ての頂点 $1,2,\dots, N$ についての隣接リストを返していることに注意する。

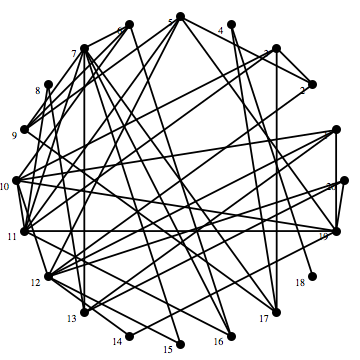
random20_0.2

構成されたグラフ g の描画には、関数 ShowGraph を使う。 オプションの VertexNumber -> On は頂点番号を表示する。 

ShowGraph[RandomGraph[20, 0.2], VertexNumber -> On]

演習： 完全グラフ、完全二部グラフ、星グラフ、ランダムツリー、ランダムグラフについてそれらを描画し、その隣接行列および隣接リストを検討しなさい。

グラフの外観

ShowGraph では、辺・頂点の色やスタイルを変更してグラフの外観を変えることができる。 

ShowGraph[SetGraphOptions[RandomTree[10], 
   {{1, VertexColor -> Red}, {6, 10, VertexColor -> Blue}}], VertexNumber -> On]

ShowGraph[SetGraphOptions[CompleteGraph[4], 
  {{1, 2, VertexColor -> Green, VertexStyle -> Disk[Large]},
   {3, 4, VertexColor -> Blue}}, EdgeColor -> Red]]

有向グラフ

グラフ構成時にオプション Type->Directed を指定して対応する有向グラフを得る。

GraphPlotの入力と描画

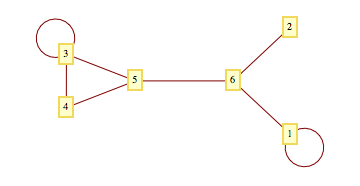
graphplot

頂点の集合$V$と辺の集合$E$で定まるグラフ $G=(V,E)$ をGraphPlotで描いてみよう。 頂点 $u$ と $v$ が辺になっていることを u -> v と記し、つぎのように入力する。 


g = GraphPlot[{1 -> 1, 4 -> 3, 5 -> 3, 3 -> 3, 5 -> 4, 6 -> 1, 2 -> 6, 6 -> 5}, 
     VertexLabeling -> True]

ここでは、分かりやすさのために頂点のラベルを付けるオプションを使っている。

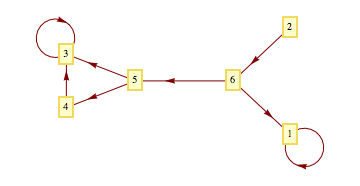
digraphplot

これを有向グラフとして表すには、オプション DirectedEdges -> True をセットする。 


dg = GraphPlot[{1 -> 1, 4 -> 3, 5 -> 3, 3 -> 3, 5 -> 4, 6 -> 1, 2 -> 6, 6 -> 5}, 
     DirectedEdges -> True, VertexLabeling -> True]

GraphPlotに与える辺情報は、隣接行列によって与えることができる。 いまの例の場合、隣接行列は次のようである。 

ad = {{1, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 1}, {0, 0, 1, 0, 0, 0}, 
      {0, 0, 1, 0, 0, 0}, {0, 0, 1, 1, 0, 0}, {1, 0, 0, 0, 1, 0}}
ad // MatrixForm
   1 0 0 0 0 0
   0 0 0 0 0 1
   0 0 1 0 0 0
   0 0 1 0 0 0
   0 0 1 1 0 0
   1 0 0 0 1 0
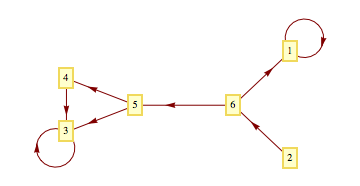
adgraphplot

こうした非対称の隣接行列であっても、有向グラフとして描画するには、オプション DirectedEdges -> True が必要である。 また、自己ループ（と多重辺）をふめるSelfLoopStyle -> True （と MultiedgeStyle -> True] ）も必要である。 


adg = GraphPlot[ad, DirectedEdges -> True, SelfLoopStyle -> True, 
    VertexLabeling -> True]

Combinatorica パッケージを使う入力と描画

ここではCombinatorica パッケージを <<Combinatorica` で読み込んでおく。

頂点の位置情報を与えず、抽象的グラフ理論的に隣接行列または隣接リストを与えてグラフを定義することもできる（描画時には、頂点の位置はMathematicaによって自動的に調整される）。 疎なグラフでは隣接リストを使う方が簡素になる。 頂点 $i$ が接続している頂点リスト $\ell_i=\{v_{i_1},\dots,v_{i_k}\}$ を全ての頂点について並べて、たとえば、上の有向グラフの隣接行列は次のように記す（リストの登場順がその番号を頂点の隣接リストである）。 

adlist = {{1}, {6}, {3}, {3}, {3, 4}, {1, 5}}

このリストは、$1\rightarrow 1$, $2\rightarrow 6$, $3\rightarrow 3$, $4\rightarrow 3$, $5\rightarrow \{3,4\}$, $6\rightarrow \{1,5\}$ と解される。 Combinatorica パッケージは、こうした隣接リストを使った有向グラフを定義することができる。 有向グラフの隣接リストであってもオプション Type -> Directed が必要である。 

fal = FromAdjacencyLists[adlist, Type -> Directed]

このグラフの隣接行列を次のように関数 ToAdjacencyMatrix を使って取り出すことができる。 その結果は、上の例で定義したリスト ad に一致していることを確認しよう。 

ToAdjacencyMatrix[fal]
   {{1, 0, 0, 0, 0, 0}, {0, 0, 0, 0, 0, 1}, {0, 0, 1, 0, 0, 0}, 
    {0, 0, 1,0, 0, 0}, {0, 0, 1, 1, 0, 0}, {1, 0, 0, 0, 1, 0}}
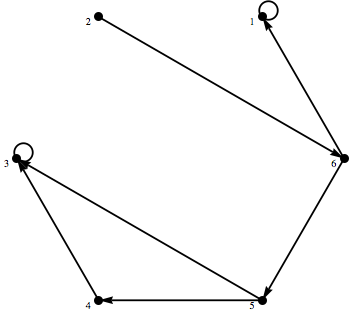fromadjlist FromAdjacencyMatrix は隣接行列からグラフを定義する関数である。 非対称な隣接行列（数学的には有向グラフを意味する）であって、有向グラフとして定義するためにはオプション Type -> Directed が必要であることに注意する。 
fad = FromAdjacencyMatrix[ad, Type -> Directed]

この有向グラフを次で描画すると左図になる。 上の例のグラフと同型であることを確かめよう。 

ShowGraph[fad, VertexNumber -> On]

グラフ構造を変更する操作

グラフ構造を変化させる基本操作には、1頂点の追加 AddVErtex（$n$個の頂点の追加には AddVertices）、1頂点の削除 DeleteVertex、辺々の追加 AddEdge（AddEdges）、辺の削除 DeleteEdge がある。 次の無向グラフ g を例にその操作を実行してみよう。 

ShowGraph[g = FromAdjacencyLists[{{2, 3}, {1, 4}, {2, 5}, {1, 5}, {1, 4}}], 
  VertexNumber -> On]

頂点の追加

グラフ g に1つの頂点を非連結的に追加するには 

AddVertex[g]

また、グラフ g に $n$個の頂点を非連結的に追加するには 

AddVertices[g,n]

辺の追加

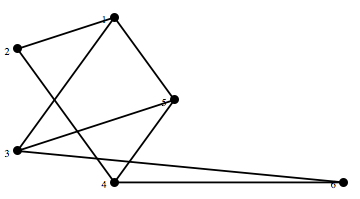
addedges

既に存在している頂点を結ぶ辺を追加するには、1本の辺なら AddEdge、複数辺なら AddEges を次のように使う。 g に1つの頂点を追加して g1 とし（その結果、追加した頂点番号 は 6 となる）、g1 に辺 {4,6} と {3,6} を追加してグラフ g2 としている。 


ShowGraph[g2 = AddEdges[g1 = AddVertex[g], {{1,5}, {4, 6}, {3, 6}}],
    VertexNumber -> On]

辺の削除

グラフの存在している辺、または辺のリストを削除するには、つぎのようにする。 

ShowGraph[g3 = DeleteEdge[g2, {1, 5}], VertexNumber -> On]

ここでは、グラフ g2 から1本の辺 {1,5} を取り除いて g3 としている。

頂点の削除

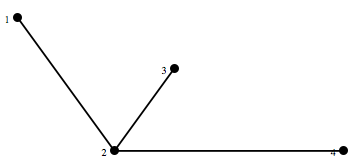
deletevertices

DeleteVertex または DeleteVertices を使うと、グラフから頂点番号（またはそのリスト）の頂点を削除して得られるグラフを次のようにして得ることができる。 頂点を削除すると、元の頂点に接続していた辺も削除されることに注意する。 


ShowGraph[g4 = DeleteVertices[g2, {1, 3}], VertexNumber -> On]