紙折り列と紙折り曲線
紙切れを折りする操作を続けて、開いてみると2種類の折れ目 $d$ と$u$ が並ん折り畳み列(folding sequence)が得られる。 $d$ は紙切れの右端を左端に反時計回りに折る操作によって得られる谷型の折れ目、$u$ は紙切れの右端を左端に時計回りに折る操作によって得られる山型の折れ目である。
2つ折り操作を繰り返す
紙切れの右端を左端に反時計回りに2つ折りにする操作を$n$回繰り返して得られる2-folding列を考える。 紙切れの左端から、得られた折り畳み列は、実際に確かめてみることができて
1回目 d 2回目 d d u 3回目 d d u d d u u ....
- $n$回目で得られる折り畳み列の長さは $2^n -1$ である。
- $n$回折った紙切れ(折り畳み列$F_n$が得られる)をさらに2つ折りにして$n+1$回折ると(折り畳み列$F_{n+1}$が得られる) \[ F_{n+1}= F_n d \tilde{F_n} \] のようになっている。
- $\tilde{F_n}$ は $F_n$ の関係で表される。
(ヒント)折れたみ記号= {d, u} Paperfoldした折り目は奇数個で、中央は常に d である。 n回折りたたんだpaperfold列は、前半は n-1回のpaperfold列 paperfold[n-1]、後半はn-1回paperfold列を逆にして記号 d と u とを入れ替えた列 Reverse[paperfold[n-1]] /. {d->u, u->d}、である。
これから、
paper2fold[1] := {d};
paper2fold[2] := {d, d, u};
paper2fold[n_Integer] :=
Flatten[{pre = paper2fold[n - 1], d,
Reverse[pre] /. {d -> u, u -> d}}]
折りたたみ曲線
$n$回折りたたんでから、折れ目が角度$\pi/2$になるようにして開いて得られる曲線を考える。
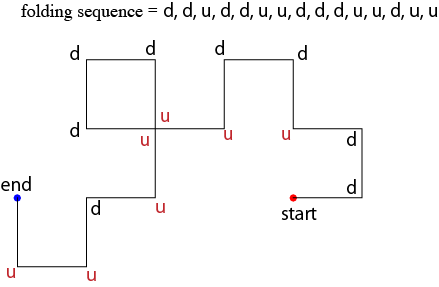
左図は、紙切れの左端を原点(赤丸)として$(1,0)$方向($x$軸方向)に伸びていた紙を3回折りたたんで得られる折り畳み列 $d, d, u, d, d, u, u, d, d, d, u, u, d, u, u$ から得られる折りたたみ曲線である。
記号 $d$ は(紙の右端に向かって)進行方向を左折($\pi/2$回転)、記号 $u$ は進行方向を右折($-\pi/2$回転)させて折れ線を書いていることに注意する。
書き出しの進行方向単位ベクトル (1,0) は folding記号列リスト lst に出会うたびに、dなら $-\pi/2$、uなら$\pi/2$回転して向きが変わっていく。 folding記号列 lst を引数とする次の関数 succesiveRotatedSum[lst] の処理を観察してみよう。 初期方法ベクトル v_1=(1,0) を与えておいて、lst要素によって定まる進行方向単位ベクトルの列 $v_1,v_2,\dots,v_{2^n}$からなるリスト(要素数は$2^n$個)を dlstとする。 次いで、この dlst を使って、$i$番目の折曲利点列 $p_i=v_1+\dots+v_i$(i=1,\dots,2^n)$ を順番に求め(dlst の連続和)、これをaddlstとする。 addlstの先頭に原点{0,0}を加えたて、Folding記号列 lst の両端点をふくめた折れ角の点列リストを返している。つまり、関数 succesiveRotatedSum[lst] は以下のようになる。
succesiveRotatedSum[lst_List] := Module[{dlst = {}, addlst = {}, R, L, v, s},
L = {{0, -1}, {1, 0}};
R = {{0, 1}, {-1, 0}};
rot[d] = L;
rot[u] = R;
v = {1, 0};
AppendTo[dlst, v];
Do[
v = rot[lst[[n]]].v;
AppendTo[dlst, v], {n, 1, Length[lst]}
];
Do[
s = Apply[Plus, Take[dlst, n]];
AppendTo[addlst, s], {n, 1, Length[dlst]}
];
PrependTo[addlst, {0, 0}];
addlst
]
たとえば、二回折りたたんだ紙の端と折れ目のいち列は次のようになる。
succesiveRotatedSum[paper2fold[2]]
{{0, 0}, {1, 0}, {1, 1}, {0, 1}, {0, 2}}
こうして得られる2次元の座標$\{x_i,y_i\}$からなるリストをLineで結んで図とすれば折り畳み直線が得られる。
Show[Graphics[Line[succesiveRotatedSum[paper2fold[2]]]]]
