箱ヒゲ図--boxplotを使う

グラフツールを正しく使うと、データ分析を効果的に行うことができる。箱ヒゲ図は、データの統計分布での外れ値を発見すること、分布が不均質ではないかを確認することなどのための視覚化表現である。

複雑な統計分析の前に箱ヒゲ図を描いて方針を立ててみよう。

データの読込

クラス平均と個人平均で取り上げた成績データ（seiseki.xlsをcsv形式としたもので、200人分の英語、国語、数学3科目得点データ）を読み込む。

> Seiseki <- read.csv("U:R/seiseki.csv", header = TRUE, skip = 8)
> str(Seiseki)
'data.frame':	200 obs. of  6 variables:
 $ Stnum: Factor w/ 200 levels "a111","a112",..: 1 2 3 4 5 6 7 8 9 10 ...
 $ Sex  : int  0 1 0 1 1 1 1 0 0 0 ...
 $ Eng  : int  68 38 51 62 82 44 48 47 77 89 ...
 $ Lang : int  76 62 62 77 69 72 72 64 77 58 ...
 $ Math : int  71 33 88 52 93 57 66 57 55 25 ...
 $ Ave  : logi  NA NA NA NA NA NA ...

基本情報の出力--summary( )

N個のデータを小さい値から大きい順に昇順に並べ、その順位を4等分する。つまり、1番目に位置する最小値(minimun)から数えてN/4番目の位置にある値(25％点)を第1四分位点(1st quartile)、N/2番目に位置する値(50％点)を中央値(median)、3N/4番目に位置する値（75％点）を第3四分位点(3rd quartile)という。 N番目に位置する値がデータセットの最大値(maximum)となる。

関数 summary( ) は変数の最小値(minimum)、第1四分位点、中央値、平均値、第3四分位点、最大値を出力する。次の例は、英語得点 Seiseki$Eng の summary出力である。

> summary(Seiseki$Eng)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  28.00   51.00   61.00   61.61   71.00   98.00

箱ヒゲ図

Seisekiの英語データ Seiseki$Eng の箱ヒゲ図を boxplot( ) を使って描いてみよう。

> boxplot(Seiseki$Eng, main = "English")

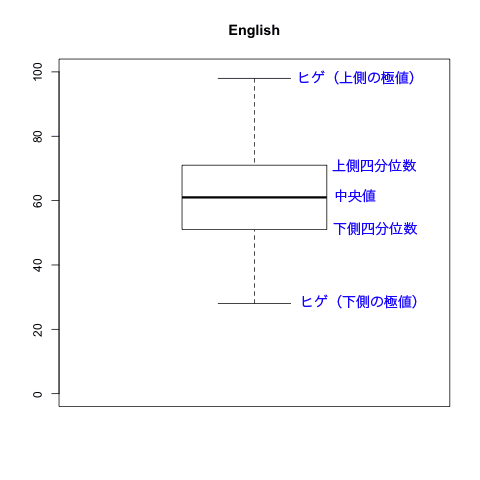すると、左図のような図が描画される。これが、英語得点の運びげ図である。

箱内部の太い中央線は中央値、箱の上側が上側四分位点（第三四分位点）、箱の下側が下側四分位点（第一四分位点）である。箱の幅（上側と下側四分位点の差）を四分位点範囲（ヒンジ散布度）という。

上下のヒゲは、それぞれ上(下)側四分位点の位置から、極値までの間を点線で結んでいる。極値とは、上(下)側四分位点から箱の幅（四分位点範囲）の 1.5 倍以内にあるデータのうちの最大値および最小値です。極値よりも大きい、または小さい値は外れ値としてひげの先にプロットされます

三科目の箱ヒゲ図

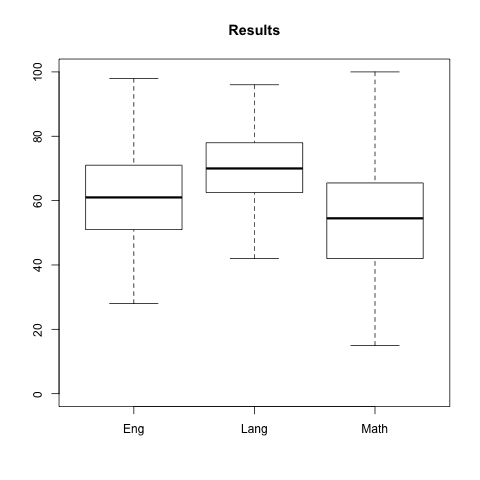
三科目の箱ヒゲ図は、たとえば、次のようにデータセット Seiseki$Eng, Seiseki$Lang, Seiseki$Math を「,」で並べて得られる。

> boxplot(Seiseki$Eng, Seiseki$Lang, Seiseki$Math, ylim = c(0, 100), names = c("Eng", "Lang", "Math"), main = "Results")

男女別得点の箱ヒゲ図

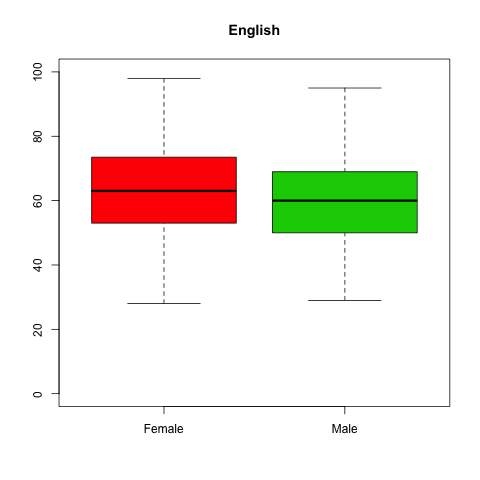
男女別の英語得点の箱ヒゲ図は次のように得られる。 col は箱の色を指定している。

>  boxplot(Eng ~ Sex, data = Seiseki, ylim = c(0, 100), col = 2:3, names = c("Female", "Male"), main = "English")