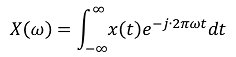
周波数ωで変換
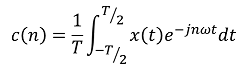
周波数ωの級数で変換
(DFT)
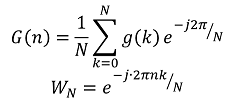
ある周波数の大きさに変換
フーリエ変換(FFT)
6回目
前回の課題についての解説
前回の課題ファイル→fft_test.c
フーリエ変換について
前回の説明では,フーリエ変換(FFT)はスペクトル(周波数ごとの成分)を算出するための計算法であると
説明しました.今回は課題として出したソースコードについて何をしているのかを説明し,フーリエ変換とは
何かについて説明を行います.
○サンプリング
もとの信号f(t)は時系列の連続した関数です.
(必ずしも連続ではありませんが,アナログという意で考えて下さい.)
サンプリングとは,ある微小時間で区切り,その時の信号の値を計測したものです.プログラムで考えれば,
その値を順次配列に入れていく処理と考えましょう.
ここでサンプリング周期Δtとすれば,0番目の配列にはf(t=0),1番目の配列にはf(t=Δt),2番目の配列
にはf(t=2Δt)・・・,といった計測データが順次入っていきます.
通常,サンプリング周期は固定されていることを基本として考えるので,1元配列にデータが格納されます.
ここで課題1で作成した関数を見てみましょう.
| void saw_wave(double* x, int n){ int i; double *p, n2; p = x; n2 = (double)n/2; for(i = 0; i < n; i++){ *p++ = ( (double)i - n2) / n2; } } なお,メイン関数内で利用するときは, double x[1024], y[1024] main(){ n=1024; saw_wave(x, n); } のように呼び出せばよい. |
これは,信号を便宜的に作り出すために作った関数ですが,1周期をn個に分割し,その時の値を配列
(ポインタで宣言)に格納するものとなっています.
さて,これまで何となくフーリエ変換とか,FFTという言葉を使ってきましたが,少し詳細を説明します.
この周波数解析に関して用語が紛らわしいので,以下のようにまとめておきます.
| 対象とする 信号の長さ |
扱う周波数 | 特徴 | |
| フーリエ変換 | 無限に続く 連続信号 |
無限の周波数のcos, sinの 重ね合わせで表現 |
任意の信号に適用できるが コンピュータでは厳密には扱えない |
| フーリエ級数展開 | 有限長の 連続信号 |
無限の周波数のcos, sinの 級数で表現 |
ある時間長※の信号に適用できる コンピュータでは厳密には扱えない ※ある時間長の信号が永遠に繰り 返されている前提 |
| 離散フーリエ変換 (DFT) |
有限長の N個の離散信号 |
有限のN個の周波数の cos, sinの大きさで表現 |
ある時間長※の信号を離散化し, その刻みに相当する周波数まで分解できる ※ある時間長の信号が永遠に繰り返されて いる前提 |
| 高速(離散) フーリエ変換(FFT) |
有限長の N個の離散信号 |
有限のN個の周波数の cos, sinの大きさで表現 |
上記同様 ただし,計算量が格段に少なくなる |
参考までに式も示しておきます.なお,詳細については,数多くの良書,記事があるので各自調査して下さい.
| 基本式 | 特徴 | |
| フーリエ変換 | 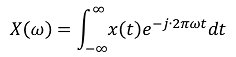 |
ある時刻tまでの信号に対して 周波数ωで変換 |
| フーリエ級数展開 | 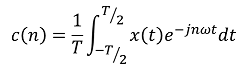 |
ある時刻tまでの信号に対して 周波数ωの級数で変換 |
| 離散フーリエ変換 (DFT) |
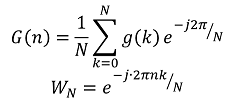 |
k番目のデータに対して ある周波数の大きさに変換 |
| 高速(離散) フーリエ変換(FFT) |
上式の回転子WnのうちN=0,1またはN=0,1,2,3で演算 | 上記の方法と結果は同じ |
○離散フーリエ変換(DFT)
フーリエ変換を行うには,長時間の信号の中でもある区間を取り出す必要があります.
ある区間,といっても離散量の場合はデータ数で区切ります.ここで区切ったデータ数をN個とおくことに
します.
時間の順に信号の大きさが並んでいるのはすでにお話しした通りです.
フーリエ変換は,時間順に並んだN個のデータをN個の周波数成分データに並べ替える計算法と考えて
ください.
正確には,N個並んだ時の周期に対して1/N刻みの周期の周波数データに並べ替えられます.
例を挙げましょう.サンプリング周波数が1kHzとします.データ数は1000個とします.
この場合,データ1000個でちょうど1秒の周期となります.フーリエ変換で1秒のデータを1000に区切って
周波数成分に分けるから1秒/(1〜1000)周期すなわち1Hzステップで並べ替えます.
あとは,各周波数の大きさを1Hzステップ(N個の周期/1周期のデータ数N)であてはめていくことで計算が
できます.あてはめるとは,相関の大きさ(どのくらい似ているか)を調べることと理解してよいと思います.
フーリエ変換の原理を知るには,DFTについて学ぶことが分かりやすいと思います.
これに対し,FFTは実用性があるので,本授業ではFFTを使うことにしました.先週お話しした通り,原理の
説明を丁寧に行うと半期の授業となるため,今回は利用するだけと致しました.
なお,DFTとFFTの違いは,計算量にあります.DFTはN2に対し,FFTはN log2(N/2)の計算を行います.
データが大きくなるほど,その違いは大きくなってきます.
ウインドウについて
まず,FFTは本当に周波数成分を的確に示しているのか?という点について考えてみましょう.下図を
ご覧ください.DFTもしくはFFTは有限個のデータを切り出して対象としているため,両端は不連続になる
ため,不要な高周波信号が出てしまいます.(矩形波,ステップ関数は瞬時に値が変化するため,周波数
∞の成分すらも含まれています.)
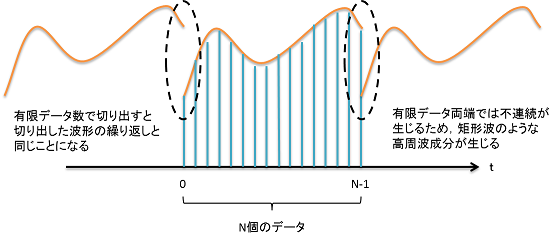
これは,仮に単一周波数のサイン波であっても起こりうる問題であり,位相がずれてしまえば,両端は
不連続になってしまいます.
この問題を解消するために,切り出したデータ数の区間に対し,重み付けを行う方法が考案され,これを
ウインドウ(窓関数)と呼んでいます.以下の概念図を見てください.上図の波形に対し,重み付けをする
ことで両端はスムースにつながるため,不連続の問題は解決できるのです.
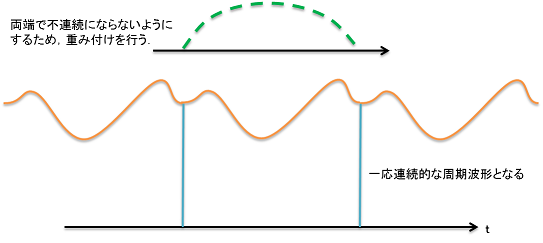
Hanning Window
以下の定義式をもとのデータにかけることで上記の処理が実現できます.
h(n)=0.5-0.5 cos(2πn/(N-1))
Hamming Window
Hanning Windowでは,両端の重みが完全にゼロであり,その近傍も反映されない問題を解決するため,
係数を変えたものが使われます.以下の定義式をもとのデータにかけます.
h(n)=0.54-0.46 cos(2πn/(N-1))
補足説明
上記のような対策を講じても,必ず正しい結果であるとは言い切れません.
FFTにおいては,例えば1024とか2048のような,2のべき乗個のデータを対象としていることを考慮する
必要があります.仮に,きっちり整数の周波数になるサイン波を対象としても,区切る周波数が,そうした
整数のようなキリのいいものでないため,必ずしも鋭いピークを持ったスペクトルになるとは言い難いから
です.
例えば,周波数10Hz(周期),サンプリング周波数50Hzだったとして,
また,ウィンドウを掛けても,元波形が不連続であり,たまたまデータの両端になる場合,正しく変換され
ない可能性があります.
以上のような性質を持っていることから,どのようにデータを切り出すかによって,大きく変換結果が変わる
可能性があることを充分に理解しておく必要があります.
課題1 前回作成した関数square_wave, saw_wave, sines_2を用い,fftの演算を行ってみよ.
手順1 メインプログラムを作成し,上記関数を呼び出して,配列にデータを入力する.
手順2 fftのプログラムを呼び出し,変換を行う.
手順3 上記プログラム中でファイルを作成し,テキストファイルを出力する.
手順4 Excelに呼び込みグラフを作ってみる.
コンソール上で*で表示させたグラフを作ったり,グラフィックを作れる余力のある人は試してみても良い.
課題2 ハニング窓,ハミング窓のプログラムを作成せよ.
関数名は以下のような名前と引数を設定するとよい.
void hanning(double* x, int n)
void hamming(double* x, int n)
プログラム自体は簡単に作れるので,その内容をよく理解しながら作成すること,
課題3 課題1のプログラムに課題2で作ったウィンドウを掛けてFFTを行い,課題1の手順で変換を行い,
結果を比較してみよう.
手順 FFTの前に課題2の関数を呼び出してウィンドウを掛ける,という処理を加える.