5回目

データ処理，信号処理について
本日から，データ処理の一つとして信号処理を扱っていきます．まずは，フーリエ変換に取り組みます．

フーリエ変換
どのような関数による変換で，どんな性質を持っていて，ということに関しては，この授業では省略します．
きちんと取り組むと数学的な説明だけで半期位の授業ができてしまう内容なのです．従って，目的と効果に
ついてのみ触れることにします．
なお，簡単にFFTに関する実演を授業中に致しますのでご覧下さい．

FFTの機能を簡単に体験する方法
内容はWindows Media Playerを用い，wavファイルを再生したときの［視覚エフェクト］を変更して
行います．
初めの操作は，右クリック→［バーとウェーブ］→［スコープ］で現波形を見ることができます．
次の操作で，右クリック→［バーとウェーブ］→［バー］で瞬間瞬間のFFT結果を時系列でみることができます．

FFTについて
ここで，ある信号波形データがあったとします．複雑な信号波形をそのまま観察していても得られる情報は
少なく，その信号にどのような周波数（振動数※）成分がどのくらいの大きさで含まれているかを解析すること
によって，どれが支配的であるか，あるいはその高調波成分はどんなものかを調べるとその性質がつかめます．
そのための方法としてフーリエ変換が用いられます．

この計算法自体は1965年頃には確立していたといわれており，計算速度を上げるために様々なアルゴリズムが
考案されています．

※周波数と振動数
どちらも単位はHzで似たようなものと考えられがちですが，厳密には使い分けています．

周波数は，電波，磁界，音などの信号を対象とした表現に用いられます．また，共振周波数の言葉の通り，
積極的に発振させる意図を持った利用がなされています．

振動数は，機械の構造物や機構の応答に用いられる表現で利用されます．また，原子や分子の運動に
関しても振動数が用いられます．固有振動数の言葉の通り，対象とする物理系の持つ特性を考え，どちらか
というと抑制したい意図を持った利用がなされています．

さて，コンピュータに信号を取り組んだ場合，ディジタル（離散）信号となります．
そのため，DFT（離散フーリエ変換）を行うことにしますが，データの大きさによっては繰り返し回数が多く計算が
重いため，フーリエ演算を高速に行う高速フーリエ変換(FFT)というアルゴリズムを利用します．
詳細は別途勉強してしていただくとして，DFTとは，比較用の信号の周波数をある小刻みで変化させていった
とき，調査対象の信号がどの位マッチしているかの度合いを算出する操作を行います．
その際，位相の影響を受けないようにするため，前回紹介したオイラーの関数を用います．（言い換えれば，
元の信号成分の位相に関する情報は消えてしまいます．）
これをグラフにすれば，横軸に周波数（振動数），縦軸には大きさ(単位は対象により長さ，電圧，音圧など)を
割り当てて表現します．
その例を示します．

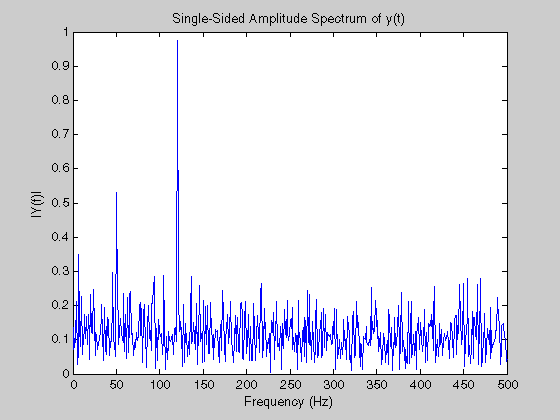
(上図の出典)http://www.mathworks.co.jp/jp/help/matlab/ref/fft.html

MATLABという数学・技術演算を行うためのソフトウェアがあり，信号波形のデータから上図のようなグラフを
生成することができます．情報処理教室のどれかにはこれがインストールされている端末がありますので，
関心のある人は試してみてください．
あるいは，皆さんが利用しているスマートフォンでもアプリがあります．

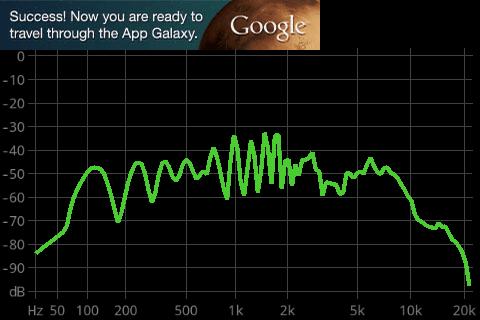
（上図の出典）http://android.allappli.net/d_com.DanielBach.FrequenSee.html

そのほか，メディアプレイヤーのソフトなどにもこれを利用した視覚効果がありますので意外と身近に利用する
ことができます．

サンプリングについて
既にご存じの方も多いと思いますがある信号をディジタルデータに変換することをサンプリングと呼びます．下図は
横軸に時間を取っていますが，ある細かい刻み（サンプリング周波数）でその時の振幅を計測します．
サンプリング周波数おきにデータが配列に格納されていきますが，基本は一次元配列です．

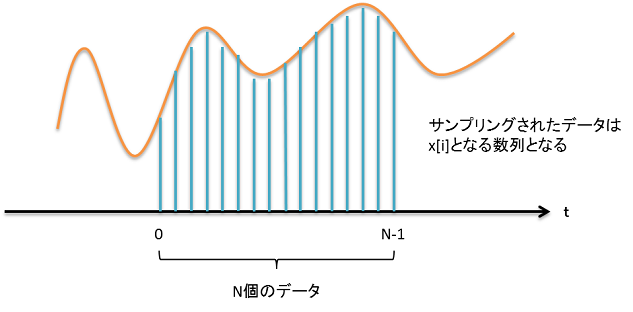
従って，どのような条件（サンプリング周波数）であったかが分からないと後で意味がなくなってしまいます．

FFTのアルゴリズム
フーリエ変換を行うための基本は，バタフライ演算という演算で，離散的波形データにおいて，あるデータの前後
何点かと加減算を繰り返しながら周波数ごとのレベルを算出していきます．細かいアルゴリズムは多様であり，
例えば以下の表のようなものが挙げられるます．
離散量を対象としているため，あるまとまったデータ数を用いて処理を行っている．FFTのアルゴリズムの計算上，
基数というキーワードがあり，この数のべき乗のデータ数の処理を行う際に計算を高速化できるというものです．
基数2ならＮ= 1024とか2048とか4096のデータをひとまとめとして利用するものであり，基数4であれば= 1024,
4096, 16384個のようなものとなっています．
ですので，配列x[N]の数列データに対して演算を行っていく処理であると，簡単に考えていただければ充分です．

来週は，以下の説明と信号波形の特性を理解した上で使うために便利な方法を紹介します．

基数	FFTの型	ビット逆転演算	計算時間比
2	2進展開型	計算時に配列に入る	1.000	基本となる基数2のFFT
2	2進展開型	利用する	0.995	上記方法からビット列逆転演算を分け，配列を直接操作せず，別途カウンタの変数を利用する
2	時間間引き型	必要	0.946	Cooley-Tukeyの方法と呼ばれるデータNを基数と偶数に分けて演算
2	非インプレイス型	不要	1.142	上記のアルゴリズムの派生形データや結果のビット列を逆順にする必要がない本来は時間のかかる処理を省略できる方法だが計算結果が速くなるわけでもない（上記は逆順にした結果を次の演算で利用できるためそれほど時間ロスがあるわけでもないため）
2	周波数間引き型	必要	0.998	Sandle-Tukeyの方法と呼ばれる偶数個データNを前半と後半に分けて演算
4	4進展開型	不要	0.897	加減算だけで計算できる原理上は基数2の3/4の時間で演算可能
2	N/2データ 2組実数データ	他のFFTと組み合わせ	0.665

どれを選ぶべきか，ということを考える際には，対象とする波形データの性質，計算機演算能力などを勘案する
必要があります．我々はアルゴリズムそのものを考えるというよりは，解析のツールとして利用するという考え方を
することが重要です．すなわち，対象とする信号の性質を理解しながら利用することに注力すべきと考えられます．

基本課題１　FFTによる解析のため，以下に挙げる関数を準備せよ．(適当なソースファイルに関数を作成せよ．)

void zero_y(double* y, int n);配列y[]のデータn個すべてを零にする．（虚数部に変な値が入っていないようにする）

int ipow2(int ｌ);2のｌ乗値を返す．（整数型で返す点が重要）

int inv2pow(int n);nが2の何乗になるかを返す．nを2で繰り返し割った回数を返せばよい．

void square_wave(double* x, int n);一周期をｎ個のデータとして矩形波を出力．振幅は任意-1～1など．
N/2までは-1，n-1までは1のように作ればいいと思います．

void saw_wave(double* x, int n);一周期をｎ個のデータとして鋸波を出力．振幅は任意-1～1など．
0で-1，n-1で1になるように直線で結べばいいと思います．

void sines_2(double* x, int n, double t1, double t2, double t3, double d1, double d2, double d3);
t1, t2, t3は周期，d1, d2, d3は無駄時間と考えてください．一周期をNとしていますが，これに対して何倍短い
周期になるかを記述します．またdは一周期をNとしてＮの何倍遅れるかを記述します．tは１より大，dは
１より小となります．例えば，
x[i]=(sin((double)i*(2.0*M_PI/t1)+(2*M_PI*d1))
　　　　+0.5*sin((double)i*(2.0*M_PI/t2)+(2*M_PI*d2))
　　　　+0.25*sin((double)i*(2.0*M_PI/t3)+(2*M_PI*d3))
0.5や0.25は適当に振幅を割り当てただけなので変更してもよい．

矩形波	鋸波

応用課題２　ダウンロードしたソースコードを整理して作成せよ．
なお，これは“時間間引き型ＦＦＴ”のアルゴリズムに関するものである．
余力があるものは，FFT（高速フーリエ変換）について調査し，どのようなものであるかを簡単にまとめて
予習しておくこと．（次回，詳細は解説する．）

ダウンロード先はここ→　fft.c

ヒントとなるキーワード，基数，バタフライ演算，スペクトル，離散フーリエ変換