微分方程式は、様々な自然現象や社会現象の記述や工学的な制御の問題等、幅広い分野で用いられています。 その重要性についてはここで語るまでもなく、微分方程式に関する授業などで深く学んでいることでしょう。 微分方程式で現象を記述することの目的は、対象とする現象の「振る舞い」を理解することにありますが、 残念ながら解析解が求められるケースは多くはありません。 そこで重要となるのが、「微分方程式の数値的解法」です。 対象とする微分方程式を数値計算により「解く」ことで、非常に簡単に微分方程式で表現した現象の「振る舞い」を 理解することが可能になります。 (もちろん、数値計算の結果が正しいかどうかについては注意深く検討する必要はありますが)
微分方程式の数値的解法については理論的な説明も含めて2年生以降でしっかりと学修していくことになると思いますが、 今回の授業では「微分方程式に慣れ親しむ」という観点から、簡単に学んでいきます。
まず初めに、「微分法方程式を数値的に解く」とはどのようなことかについて簡単に見ていきましょう。 以下のような常微分方程式の初期値問題を考えます。
\begin{align*} \dfrac{d x(t)}{dt} &= f(x(t),t), \\ \\ x(0) &= x_0 \end{align*}
これを「数値的に解く」ために、時間刻み $h$ で少しずつ時間を進めながら、
それに対する $x(t+h)$ の値(数値解)を計算することを考えます。
以下では数値解と解析解を明確に区別するために、数値解を $X(t)$、解析解を $x(t)$と書くことにします。
このとき、数値解 $X(t)$ は以下のように書くことができます。
\begin{align*} X(t+h) &= X(t) + h \phi (X(t),t) \\ \\ X(0) &= x_0 \end{align*}
これを数値計算のためのアルゴリズムとしてもっと見やすくするならば、ステップ数 $i$ を用いて以下のように書けます。
\begin{align*} X_{i+1} &= X_i + h \phi (X_i,t_i) \\ \\ X_0 &= x_0 \end{align*}
ここで、$t_i = h \times i$、$X_i = X(t_i)$ となっています。
上の表式を見ると、$\phi(X_i, t_i)$ をどのように表すか(計算するか)が 常微分方程式の数値計算のポイントになっていることが分かります。 今回の授業では、この $\phi(X_i, t_i)$ の部分の計算方法として、 オイラー法、ホイン法、ルンゲクッタ法の3つの数値計算法を試していくことにしましょう。
オイラー法の数値計算法を理解するために、以下の $x(t+h)$ のテイラー展開を考えます。 $h$ を十分に小さい値として $h^2$ 以上の項を無視すると以下のようになります。
\begin{align*} x(t+h) &= x(t) + h \dfrac{dx}{dt} + \dfrac{h^2}{2 !} \dfrac{d^2 x}{d t^2} + \cdots \\ \\ &\approx x(t) + h \dfrac{dx}{dt} \\ \\ &= x(t) + h f(x(t),t) \end{align*}
これを数値解 $X_i+1$ に書き換えると、以下のようなオイラー法の表式が得られます。
\begin{align*} X_{i+1} &= X_i + h f(X_i, t_i) \\ \\ X_0 &= x_0 \end{align*}
それでは次に、オイラー法を用いて実際に以下の微分方程式を数値的に解いてみましょう。
\begin{align*} \dfrac{dx}{dt} &= - 4 (t-1) x \\ \\ x(0) &= e^{-2} \end{align*}
ちなみに解析解は、$x(t) = e^{-2(t-1)^2}$ になります(各自自分で計算して確かめてください)。
以下にオイラー法によるプログラムを示します。グラフの描画では、オイラー法による数値解とあわせて 解析解(Exact)による結果もあわせて描画しています。
# オイラー法
import numpy as np
import matplotlib.pyplot as plt
# f(x,t)を計算する関数
def func_f(x, t):
f = -4 * (t-1) * x
return f
# オイラー法で繰り返し計算する関数
def Euler(func, x, x0, t, cnt, dt):
xp = x0
x.append(xp)
for i in range(0, cnt-1):
# オイラー法での計算
k1 = func(xp,t[i])
xp += k1*dt
# 数値解 x に追加
x.append(xp)
# 開始時刻 t_0、終了時刻 t_end、時間刻み h の設定
t_0 = 0.0
t_end = 1.0
h = 0.05
# 初期値 x_0 の設定
x_0 = np.exp(1)**(-2)
# 数値解を代入するリストの定義
x_e = []
# 時間刻み h による各時刻 t の取得
# np.linspace(a,b,c)は、初項 a, 最終項 b, 項数
t_cnt = int((t_end-t_0)/h) + 1
t = np.linspace(t_0, t_end, t_cnt)
# オイラー法により繰り返し計算
Euler(func_f, x_e, x_0, t, t_cnt, h)
# 解析解の計算
# 解析解を滑らかな曲線として表示するために、時間を100分割
t_a = np.linspace(t_0, t_end, 100)
# 解析解
x_a = np.exp(-2*(t_a-1)**2)
# グラフの描画
plt.plot(t_a,x_a, label="Exact")
plt.plot(t,x_e,marker=".",label="Euler (h=0.05)")
plt.xlabel("t")
plt.ylabel("x(t)")
plt.legend()
plt.show()
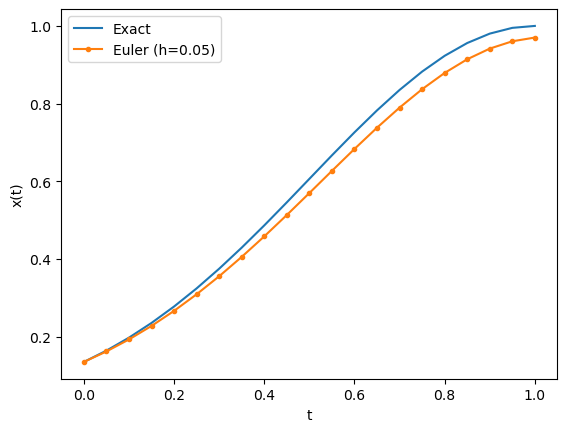
このプログラムを実行すると、下のようなグラフが得られます。 $h = 0.05$ のときには、数値解が解析解とほどほどにあっている様子が分かります。

刻み幅 $h$ の値を変化させた場合の結果は以下のようになり、$h$ の値が大きくなるに従い
数値解と解析解のズレが大きくなることが分かります。
残念ながら、オイラー法は誤差が非常に大きい数値計算法で、通常の数値計算で使われることはほとんどありません。
次に、ホイン法による数値計算法を見てみましょう。 ホイン法は、修正オイラー法や2次のルンゲ・クッタ法などと呼ばれることもあります。 修正オイラー法という別名の通り、オイラー法よりも精度が上がった数値計算法になります。
ホイン法の数値計算アルゴリズムは、以下のような表式になります。
\begin{align*} X_{i+1} &= X_i + \dfrac{h}{2} \left[ f(X_i, t_i) + f(X_{i+1}, t_{i+1}) \right] \\ \\ X_0 &= x_0 \end{align*}
第1式右辺の $f(X_{i+1}, t_{i+1})$ 内の $X_{i+1}$ は左辺の $X_{i+1}$ とは別物で、
オイラー法 $X_{i+1} = X_i + h f(X_i, t_i)$ により計算された値になります。
つまり、ホイン法はオイラー法より精度を上げるために、オイラー法の結果とオイラー法により計算された1ステップ先の計算結果を用いています。
# ホイン法
import numpy as np
import matplotlib.pyplot as plt
# f(x,t)を計算する関数
def func_f(x, t):
f = -4 * (t-1) * x
return f
# ホイン法で計算する関数
def Heun(func, x, x0, t, cnt, dt):
xp = x0
x.append(xp)
for i in range(0, cnt-1):
# ホイン法での計算
k1 = func(xp,t[i])
x1 = xp + k1*dt
k2 = func(x1,t[i+1])
xp += (k1+k2)*dt/2.0
# 数値解 x に追加
x.append(xp)
# 開始時刻 t_0、終了時刻 t_end、時間刻み h の設定
t_0 = 0.0
t_end = 1.0
h = 0.1
# 初期値 x_0 の設定
x_0 = np.exp(1)**(-2)
# 数値解を代入するリストの定義
x_h = []
# 時間刻み h による各時刻 t の取得
# np.linspace(a,b,c)は、初項 a, 最終項 b, 項数
t_cnt = int((t_end-t_0)/h) + 1
t = np.linspace(t_0, t_end, t_cnt)
# ホイン法により繰り返し計算
Heun(func_f, x_h, x_0, t, t_cnt, h)
# 解析解の計算
# 解析解を滑らかな曲線として表示するために、時間を100分割
t_a = np.linspace(t_0, t_end, 100)
# 解析解
x_a = np.exp(-2*(t_a-1)**2)
# グラフの描画
plt.plot(t_a,x_a, label="Exact")
plt.plot(t,x_h,marker=".",label="Heun (h=0.1)")
plt.xlabel("t")
plt.ylabel("x(t)")
plt.legend()
plt.show()
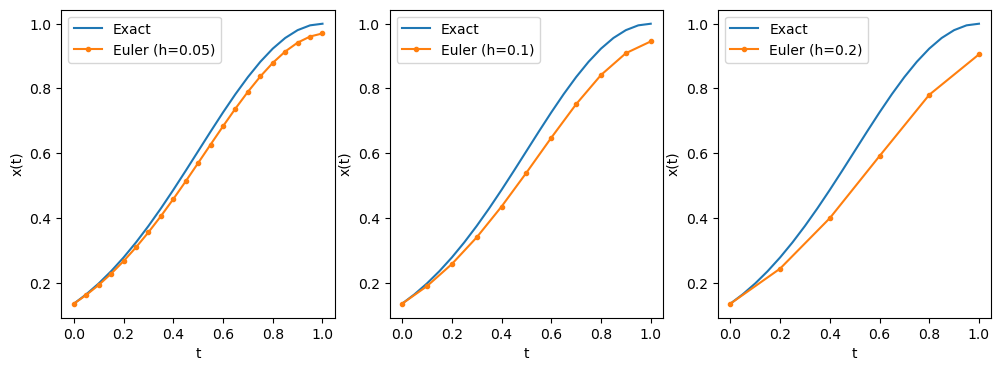
下の図では刻み幅を $h=0.1$ としていますが、オイラー法と比べて解析解により近づいていることが分かります。
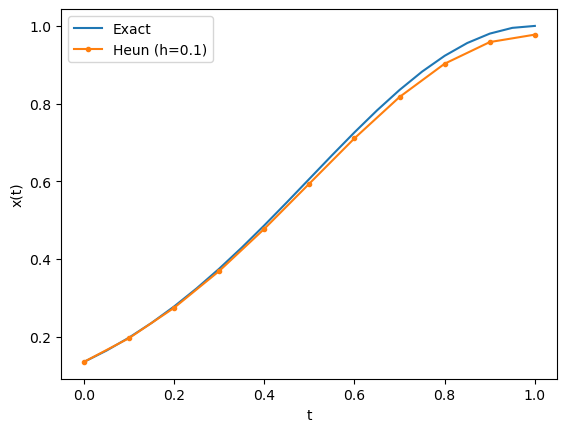
このように精度の良い数値計算方法を用いることで、より正確な数値解を求められるのはもちろんのこと、 大きな刻み幅、つまり少ない反復回数でも程よい計算結果が得られるようになることが期待できます。
ホイン法よりさらに精度が高い数値計算法として、ルンゲ・クッタ法(4次のルンゲ・クッタ法)があります。 常微分方程式の数値解法としては、通常はこの方法が使われます。
ルンゲ・クッタ法の数値計算アルゴリズムはホイン法よりさらに複雑で、以下のような表式になります。
\begin{align*} X_{i+1} &= X_i + \dfrac{h}{6} \left[ k_1 + 2 k_2 + 2 k_3 + k_4 \right] \\ \\ X_0 &= x_0 \\ ただし、 \\ k_1 &= f(X_i, t_i), \\ k_2 &= f(X_i + \frac{h}{2} k_1, t_i + \frac{h}{2}), \\ k_3 &= f(X_i + \frac{h}{2} k_2, t_i + \frac{h}{2}), \\ k_4 &= f(X_i + h k_3, t_i + h). \end{align*}
かなり複雑で分かりづらいですが、プログラムにすると以下のようになります。
# ルンゲ・クッタ法
import numpy as np
import matplotlib.pyplot as plt
# f(x,t)を計算する関数
def func_f(x, t):
f = -4 * (t-1) * x
return f
# ルンゲ・クッタ法で計算する関数
def RK4(func, x, x0, t, cnt, dt):
xp = x0
dt2 = 0.5*dt
x.append(xp)
for i in range(0, cnt-1):
# ルンゲ・クッタ法での計算
k1 = func(xp,t[i])
x1 = xp + k1*dt2
k2 = func(x1,t[i]+dt2)
x2 = xp + k2*dt2
k3 = func(x2,t[i]+dt2)
x3 = xp + k3*dt
k4 = func(x3,t[i+1])
xp += (k1+2.0*k2+2.0*k3+k4)*dt/6.0
# 数値解 x に追加
x.append(xp)
# 開始時刻 t_0、終了時刻 t_end、時間刻み h の設定
t_0 = 0.0
t_end = 1.0
h = 0.2
# 初期値 x_0 の設定
x_0 = np.exp(1)**(-2)
# 各時刻および数値解を代入するリストの定義
t = []
x_r = []
# 時間刻み h による各時刻 t の取得
# np.linspace(a,b,c)は、初項 a, 最終項 b, 項数
t_cnt = int((t_end-t_0)/h) + 1
t = np.linspace(t_0, t_end, t_cnt)
# ルンゲ・クッタ法により繰り返し計算
RK4(func_f, x_r, x_0, t, t_cnt, h)
# 解析解の計算
# 解析解を滑らかな曲線として表示するために、時間を100分割
t_a = np.linspace(t_0, t_end, 100)
# 解析解
x_a = np.exp(-2*(t_a-1)**2)
# グラフの描画
plt.plot(t_a,x_a, label="Exact")
plt.plot(t,x_r,marker=".",label="RK4 (h=0.2)")
plt.xlabel("t")
plt.ylabel("x(t)")
plt.legend()
plt.show()
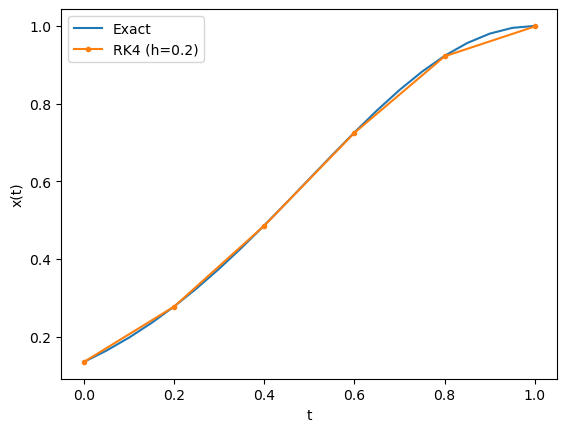
下の図では刻み幅を $h=0.2$ としていますが、解析解と非常によく一致していることが分かります(ほぼ重なってしまっている)。
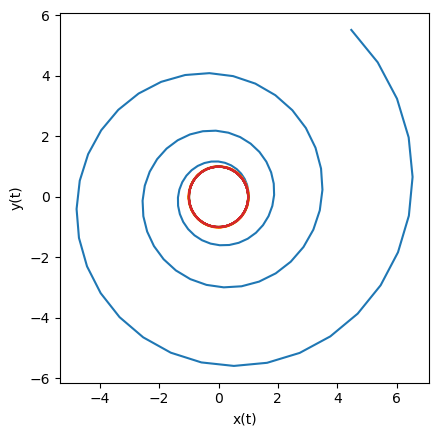
ここまで、1変数の常微分方程式の数値解法について見てきましたが、2変数以上でも考え方は全く同じです。 ここでは、以下の円軌道の連立微分方程式を考えてみましょう。
\begin{align*} \dfrac{dx}{dt} = f(x,y,t) = - y, \dfrac{dy}{dt} = g(x,y,t) = x \\ x(0) = 1, y(0) = 0 \\ \end{align*}
上の方程式の解は、$x(t) = \cos (t)$, $y(t) = \sin (t)$になります。
これをオイラー法の数値計算アルゴリズムで表してみましょう。$x(t),y(t)$の数値解をそれぞれ$X, Y$として、以下のようになります。
\begin{align*} X_{i+1} &= X_i + h f(X_i, Y_i, t_i) = X_i - h Y_i \\ \\ Y_{i+1} &= Y_i + h g(X_i, Y_i, t_i) = Y_i + h X_i \\ \\ X_0 &= 1 \\ Y_0 &= 0 \end{align*}
変数が増えただけで、本質的には1変数と全く同じなのが分かります。
ただし、$X_{i+1}, Y_{i+1}$の計算順序に気をつけてください。
$X_{i+1}$ を計算した後に 関数 $g$ の値を計算しようとすると、$g(X_{i+1},Y_i,t_i)$ として
計算してしまうことになります。
先に $g(X_i,Y_i,t_i)$ の計算を行なった上で、その値を何らかの値に代入してから $X_{i+1}$ の計算をするようにしましょう。
次に、ホイン法でのアルゴリズムを表してみましょう。これも見た目は複雑になっていますが、本質的には1変数の時と同じです。
\begin{align*} X_{i+1} &= X_i + \dfrac{h}{2} \left[ k_{1x} + k_{2x} \right] \\ \\ Y_{i+1} &= Y_i + \dfrac{h}{2} \left[ k_{1y} + k_{2y} \right] \\ \\ X_0 &= 1 \\ Y_0 &= 0 \\ ただし、 \\ k_{1x} &= f(X_i, Y_i, t_i) = - Y_i, \\ k_{2x} &= f(X_i + h k_{1x}, Y_i + h k_{1y}, t_i + h) = - (Y_i + h k_{1y}) = - (Y_i + h X_i), \\ k_{1y} &= g(X_i, Y_i, t_i) = X_i, \\ k_{2y} &= g(X_i + h k_{1x}, Y_i + h k_{1y}, t_i + h) = X_i + h k_{1x} = X_i - h Y_i. \end{align*}
ルンゲ・クッタ法についてはここでは記しませんが、オイラー法やホイン法と全く同じ考え方になります。
plt.axes().set_box_aspect(1)
を加えると縦横の比率が同じになり、下に表示しているようなグラフを描画できる。1変数との違いは、右辺の計算が$f(x,y),g(x,y)$の2つあるので、それに合わせて関数も2つ用意すると分かりやすい。
余裕のある人向けオイラー法、ホイン法の結果に加えて、ルンゲ・クッタ法での結果も合わせて表示させてみよ。

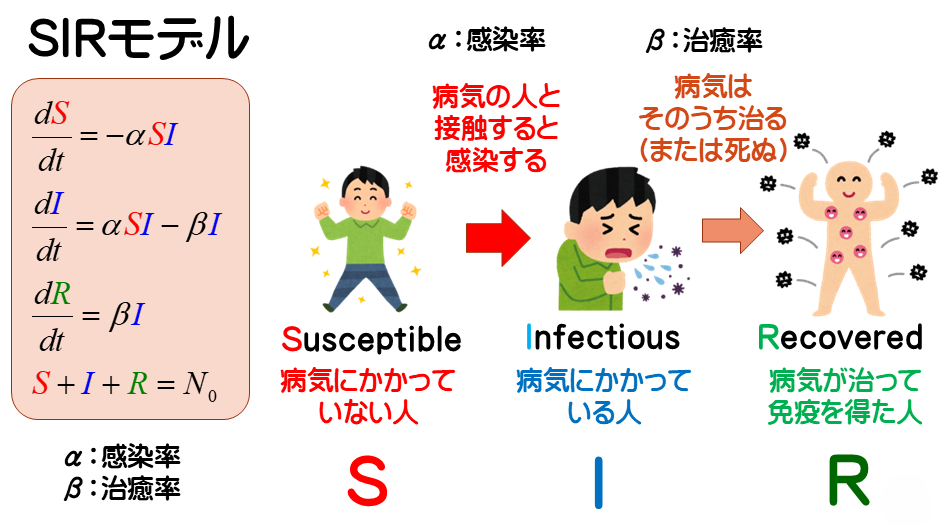
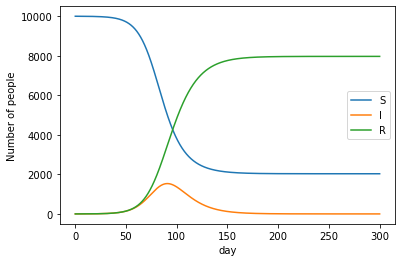
感染症の広がりを表す数理モデルである SIR モデルについて、ホイン法またはルンゲクッタ法で実装してみよ。 SIR モデルは、Sが未感染者、Iが感染者、Rが免疫獲得者(あるいは死者)として、以下の3変数連立微分方程式で表される。 ただし、$S(t)+I(t)+R(t) = N_0$(一定)であることに注意。
\begin{align*} \dfrac{dS(t)}{dt} &= - a S(t) I(t), \\ \dfrac{dI(t)}{dt} &= a S(t) I(t) - b I(t), \\ \dfrac{dR(t)}{dt} &= b I(t), \\ \end{align*}
初期値およびパラメータは、例えば以下のものを利用して計算してみよ。
\begin{align*} &S(0) = 9999, \quad I(0) = 1, \quad R(0) = 0, \quad (N_0 = 10000) \\ &a = 0.2 / N_0, \quad b = 1.0 / 10.0\\ &h = 0.01 \end{align*}
「課題1」について作成したプログラムを提出してください。
余裕がある人は、「課題2」の内容も同じファイル内に加えて提出してください。
ただし、コメント文として
学生番号、名前、プログラムの簡単な説明
を書く事。
ファイル名は、9-rep.ipynb として、 提出したファイル単体で実行できるようにすること。
提出締め切り: 2024年12月2日19時