第１０回 Pythonによる現象のシミュレーション１（2024年12月9日）

今日の内容

粒子のランダムウォークモデル（1次元、おさらい）

直線上に１つの粒子があるとします。 この粒子が時間とともに左右に移動するのですが、その移動が完全にでたらめである場合、 その運動をランダムウォーク（または、酔歩、乱歩などとも呼ぶ）と呼びます。 ここでは、そのような粒子の運動をコンピュータを使って再現することにします。 （２次元平面、３次元空間、あるいはn次元空間においても同様にランダムウォークを定義できます。）

まず、いくつか仮定をもうけておきます。 粒子は微小時間 $\Delta t$ の間に微小距離 $\Delta x$ だけ左右に進むか、その場に留まるとします。 ここで、その場に留まるか、左右どちらかに移動するかは完全にでたらめ（ランダム）であるとします。 ここでは、0, 1, 2 のみが等確率で出る乱数を用いて、

といった運動（１次元ランダムウォーク）を考え、コンピュータ上でシミュレーションしてみましょう。

今、離散的な時刻を t とし（t = 0,1,2,3,・・・,N）、時刻 t における粒子の位置を x とすると、 Python のコードは以下のようになります。
ここで、時刻 t = 0 ~ N までの位置 x を記憶するリストの要素数は N + 1 であることに注意しましょう。 

# １次元ランダムウォーク
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt


N = 100

# 乱数のシードを指定（結果の再現性を得るためには必要）
rd.seed(1)

# 0~2の整数をランダムにN個生成して、リスト r に格納
r = rd.randint(0,3,N)

# 粒子の位置 x のリスト生成（値を全て０にして生成＆初期化）
x = np.zeros(N+1)
x[0] = 0

# ランダムウォークの実行
for i in range(N):
  # 0なら、1つ前に移動
  if r[i] == 0:
    x[i+1] = x[i] + 1
  # 1なら、1つ後ろに移動
  elif r[i] == 1:
    x[i+1] = x[i] - 1
  # それ以外（2）なら、移動せず
  else:
    x[i+1] = x[i]

# 時刻 t を格納したリストの生成（0~Nまでの整数を順に格納）
t = np.arange(N+1)


plt.plot(t,x)
plt.xlabel("t")
plt.ylabel("x")
plt.legend
plt.show()

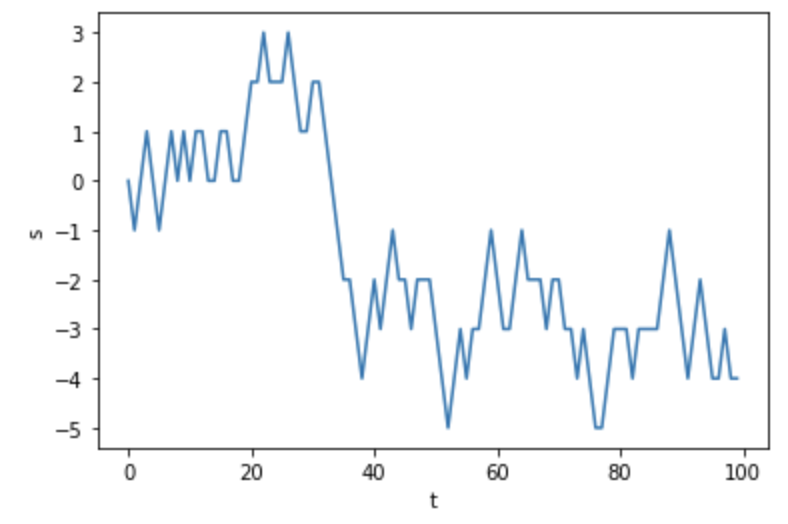
実行すると下のようなグラフが描画されます。

周期境界条件下における粒子のランダムウォークのアニメーション（1次元）

先ほどの設定では、位置 x の値に制限はありませんでした。 つまり、いくらでも大きくなったり小さくなったりする可能性がありました。（もちろん、繰り返し回数 N に依存しますが）
しかし、現実の問題を考える際には領域の大きさに制限があることは当たり前ですから、 粒子が移動できる範囲、つまり 位置 x がとれる範囲に制限を設ける必要があります。 例えば、 -XMAX ≦ x ≦ XMAX として （XMAXは正定数）１次元格子をある有限な長さとします。 このとき、境界（x==-XMAX または x==XMAX）に粒子が到達した場合にどう処理するかを考える必要があります。

境界での処理は、例えば以下の様なものが考えられます。

ですが、ここでは以前も考えた「境界をはみ出す方向に進んだ場合には、反対側の境界へと移動する」という条件、 つまり「周期的境界条件」を考えてみることにしましょう。
以下では、XMAX = 5, N = 200 として周期的境界条件下におけるランダムウォークを実装してみましょう。 

# １次元ランダムウォーク
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt


N = 200
XMAX = 5

# 乱数のシードを指定（結果の再現性を得るためには必要）
rd.seed(1)

# 0~2の整数をランダムにN個生成して、リスト r に格納
r = rd.randint(0,3,N)

# 粒子の位置 x のリスト生成（値を全て０にして生成＆初期化）
x = np.zeros(N+1)
x[0] = 0

# ランダムウォークの実行
for i in range(N):
  # 0なら、1つ前に移動
  if r[i] == 0:
    x[i+1] = x[i] + 1
  # 1なら、1つ後ろに移動
  elif r[i] == 1:
    x[i+1] = x[i] - 1
  # それ以外（2）なら、移動せず
  else:
    x[i+1] = x[i]

  # 境界条件の処理
  # 左にはみ出た場合
  if x[i+1] < -XMAX:
      x[i+1] = XMAX
  # 右にはみ出た場合
  elif x[i+1] > XMAX:
      x[i+1] = -XMAX

# 時刻 t を格納したリストの生成（0~Nまでの整数を順に格納）
t = np.arange(N+1)


plt.plot(t,x)
plt.xlabel("t")
plt.ylabel("x")
plt.legend
plt.show()

以下のようになり、-5 および 5 を超えることなく、境界を跨いで反対側に移動（ワープ？）していることが分かります。

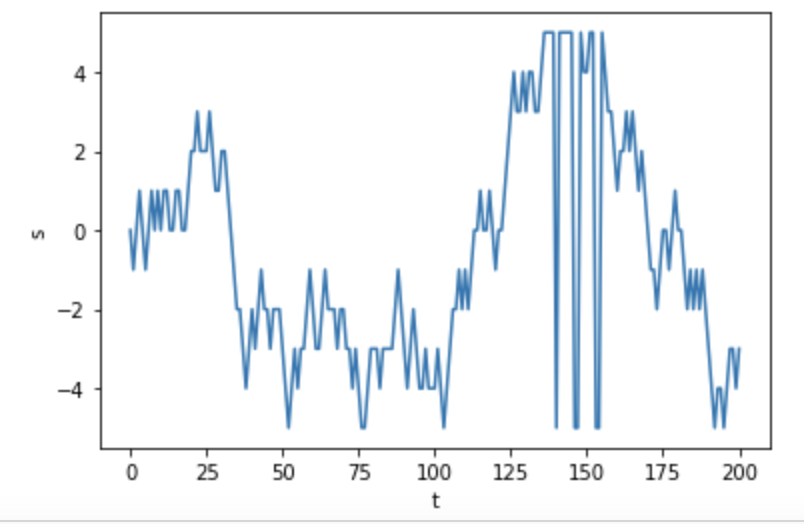
さらに、境界を跨いだ移動をより分かりやすくするために、アニメーションを作成してみましょう。 

# １次元ランダムウォーク
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from IPython.display import HTML


N = 200
XMAX = 5

# 乱数のシードを指定（結果の再現性を得るためには必要）
rd.seed(1)

# 0~2の整数をランダムにN個生成して、リスト r に格納
r = rd.randint(0,3,N)

# 粒子の位置 x の初期化
# （今回の場合はアニメーションにするので過去の履歴は保持する必要がないのでリストにしなくてもOK）
x = 0

# 時刻 t を格納したリストの生成（0~Nまでの整数を順に格納）
t = np.arange(N+1)


# グラフの描画領域を作成
fig = plt.figure(figsize=[12,2])


# 描画領域内での描画場所を指定（1行1列で配置）
ax = fig.add_subplot(1,1,1)



# 各軸のラベル
ax.set_xlabel("x", fontsize=15)

# グラフの表示域の設定
ax.set_xlim([-XMAX,XMAX])
ax.set_ylim([-1,1])



# グラフ描画のために、空のリスト作成
p=[]

# 初期化のための関数（初期位置描画のために必要）
def PlotInit_1D():
  # 現在の位置をplot
  p.append(ax.scatter(x,0,c="red",s=100))


# ランダムウォークの実行するための関数
def PlotRW_1D(i):
  # xの値を保持するため
  global x

  # 描画が重ならないようにするための処理
  if len(p) > 0:
    p.pop().remove()
  # 現在の位置をplot
  p.append(ax.scatter(x,0,c="red",s=100))

  # 0なら、1つ前に移動
  if r[i] == 0:
    x = x + 1
  # 1なら、1つ後ろに移動
  elif r[i] == 1:
    x = x - 1
  # それ以外（2）なら、移動せず(これは本当は書かなくても問題ない)
  else:
    x = x

  # 境界条件の処理
  # 左にはみ出た場合
  if x < -XMAX:
    x = XMAX
  # 右にはみ出た場合
  elif x > XMAX:
    x = -XMAX



# FuncAnimationとしてアニメーションを作成
anim = animation.FuncAnimation(fig,PlotRW_1D,init_func=PlotInit_1D,frames=range(N),interval=50,repeat=False)


# Notebook 上で表示するためのおまじない
plt.close()
HTML(anim.to_jshtml())

実行すると以下のようになり、枠の中を粒子（赤い丸）が左右に移動する様子がアニメーションで表示されます。

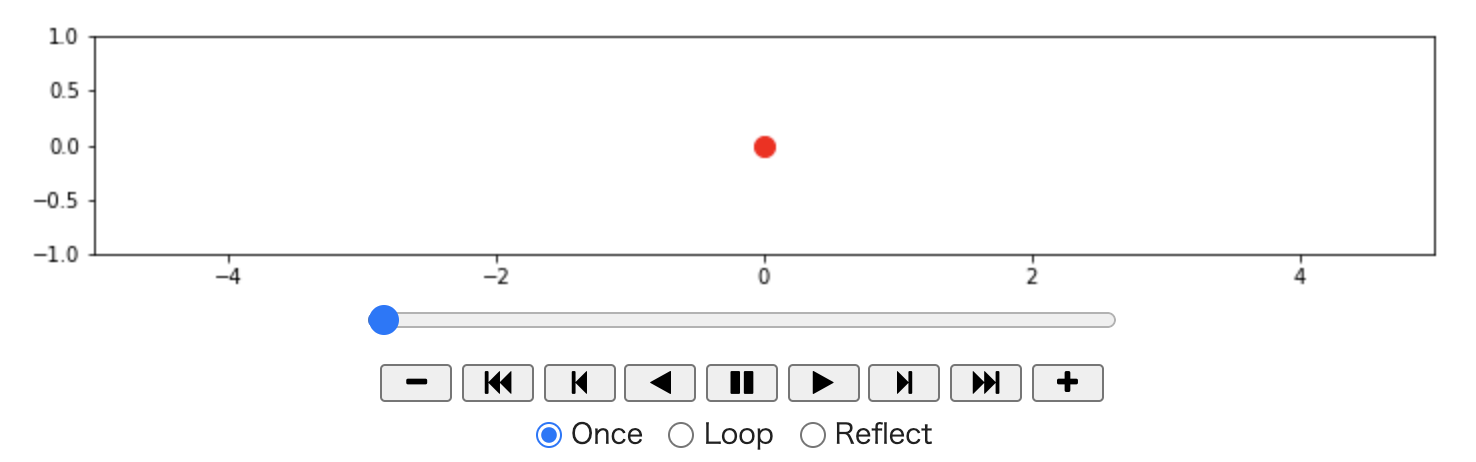
ここでは、アニメーションを作成するための手法として FuncAnimation を用いております。 以前に紹介した ArtistAnimation との主な違いは、繰り返し処理のたびにグラフを生成して保持しておくのではなく、 繰り返し処理を関数として呼び出すことにあります。 関数の使い方が苦手な人にとっては難しく感じるかもしれませんが、 for 文や while 文といった繰り返し処理の構文を書く代わりに、繰り返し処理の関数を作っていると理解してしまって問題ありません。

主な引数の意味は、以下の通りです。

詳しくは、こちら の公式 Reference を参照のこと。

粒子の２次元ランダムウォーク

上で扱った１次元モデルと同様に、粒子の２次元ランダムウォークを考えてみましょう。

問題

２次元の格子上に、粒子が１つあるとする。 この粒子の位置を $(x, y)$ とする ($x, y$ は整数)。 この粒子が２次元格子上をランダムウォークするとき、(x, y) の時間発展はどのようになるか調べよ。 さらに、粒子の動きをアニメーションにして観察せよ。

　

今、二次元格子上に粒子があるとし、その粒子の運動はランダムであるとします。 つまり、次の時刻に、「現在の場所に留まる」、「右に移動する」、「左に移動する」、「下に移動する」、「上に移動する」 ことが等確率で起こるとします（もちろん等確率でない場合も考えられます）。 0〜4のが出る乱数があると考えやすいでしょう。念のため書けば、それを用いて、

といった状況です。

今、離散的な時刻を t とし（t = 0,1,2,3,・・・,N）、時刻 n における粒子の位置を $(x, y)$ とします。 t = 0 での粒子の位置（初期位置）を ($x_0, y_0$) とします。 ただし、今回はアニメーションとして画面に表示したいので、$x$ および $y$ には取りうる値に範囲を設けます （画面には有限の領域しか表示できないため）。 具体的には、

$0 \leqq x \leqq$ XMAX, $0 \leqq y \leqq$ YMAX

としましょう。（XMAX, YMAX は正の整数）

このとき、時間を進めると、粒子はランダムウォークし、ふらふらと動きますが、 上記範囲を超えた場合どうするかが問題となります（境界条件と呼ぶ）。 対処の仕方は数種類考えられますが、以下の課題では周期的境界条件を考えることにしましょう。

◎課題1

２次元格子上での粒子のランダムウォークシミュレーションのプログラムを作成せよ。 ただし、境界条件は周期境界条件とし、粒子の移動範囲や時刻は以下のようにせよ。

XMAX = 10, YMAX = 10, N = 200, $x_0$ = XMAX / 2, $y_0$ = YMAX / 2

課題2

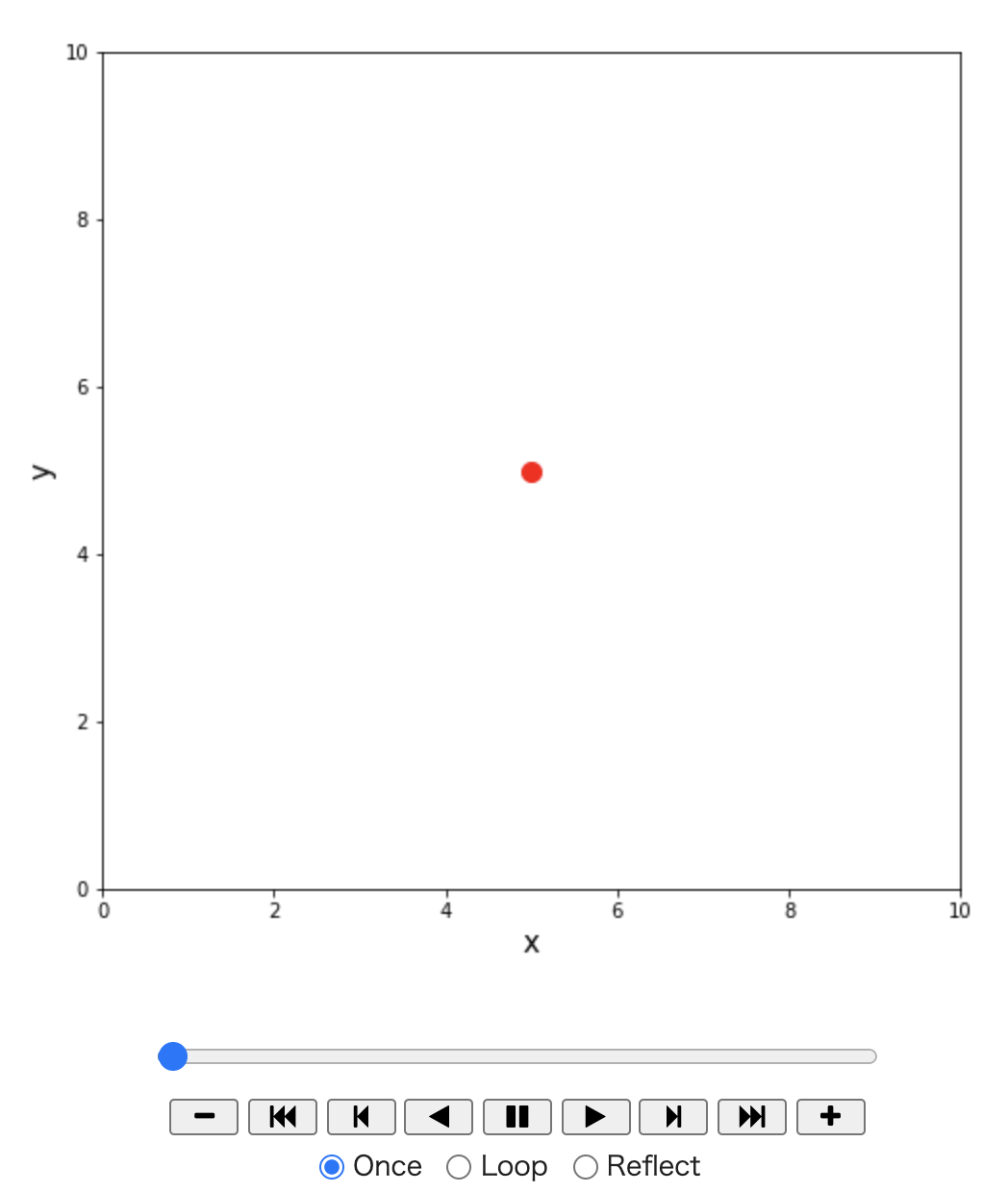
上の課題では、全ての方向に等確率で移動することになっていたが、 例えば右への移動確率が少し高いといった場合は、粒子はどのような運動を示すだろうか？ 例えば、0〜5の乱数が出るときに、

といった場合についてプログラムを作成し、実験してみよ。
ただし、境界条件は反射境界条件とする。

課題3（さらなる理解の為に）

粒子がどのように移動したかその軌跡を見たいとする。 どのようなプログラムを書けば良いだろうか？ 実際に作成してみよ。

レポート課題

「課題１」について作成したプログラムを提出してください。
余裕がある人は、「課題２」の内容も同じファイル内に加えて提出してください。

ただし、コメント文として

学生番号、名前、プログラムの簡単な説明

を書く事。

ファイル名は、10-rep.ipynb として、 提出したファイル単体で実行できるようにすること。

提出締め切り：　2024年12月9日19時

戻る