二項分布の式
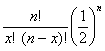
には階乗が含まれるため、そのまま計算しようとすると、試行回数nが大きくなるほど、膨大な計算量になってしまう。しかし一方で、nが大きくなるほど二項分布は正規分布に近づいていくので、正規分布で近似することができる。 (なぜ正規分布に近づくのか、という議論は、長くなるので、残念ながらここでは省略する。)
正規分布 normal distribution は、一般に
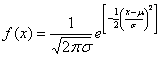
で表される。なかなかややこしい式だが、平均μ=0、分散σ=1なら、
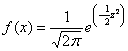
となって、計算しやすくなる。これが標準正規分布 standard normal distribution である。
二項分布では
平均はnp
分散はnp(1-p)
になるので、n回の試行でx回「以下」「1」が出る場合の確率を
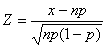
として、平均が0、分散が1の標準正規分布で近似して計算することができる。この式では、分子で平均値を0に補正して、分母で分散を1に補正している。