スマートコミュニティ全体最適化概要
スマートコミュニティモデル全体の概要図を図1に示す。また,以下に各分野の決定変数,従属変数,定数と制約条件の関係を示す。
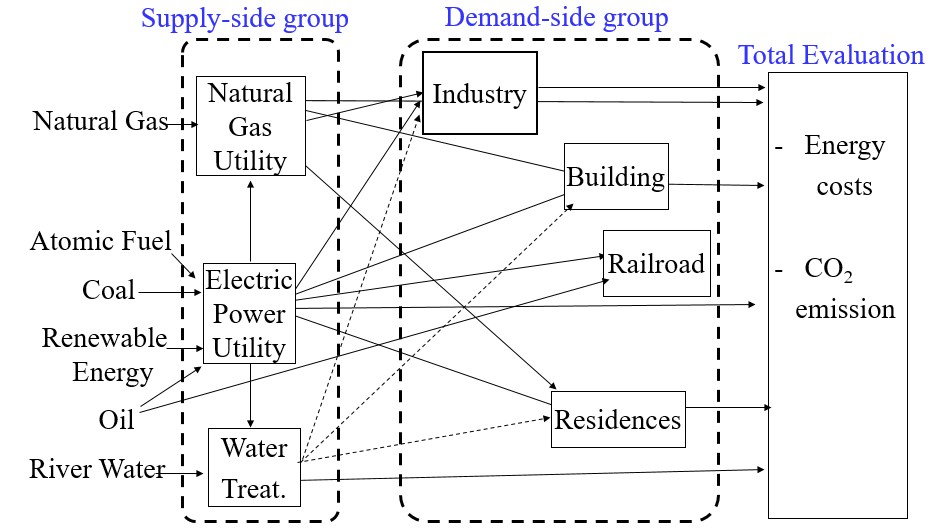
図1スマートコミュニティモデル全体概要図(1)
・決定変数,従属変数,定数と制約条件の関係
(1)産業分野モデル(2)
産業分野のモデル概要図をFig. 2に示す。図中に決定変数(■),従属変数(●),定数(▲)を示す。産業モデルでは電力,蒸気,熱エネルギーを扱う。Fig.
1において,各時間帯の電力,蒸気,熱のエネルギーバランスについては,システム構成図の各々のエネルギー毎の接続状態によって決まる。例えば,電力エネルギー供給は,購入電力,GTG発電量,PV出力,蓄電池出力からなる。また,電力エネルギー消費は,ターボ冷凍機への電力入力,蓄電池への電力入力からなる。エネルギーバランス制約は本文(2)式で表現できるが,決定変数の設備が停止(y_i=0)の場合は,この設備決定変数(z)が0となり((4)式より),この設備を除いた設備でシステム構成に応じたバランス式を用いる。Fig.2の各設備の特性をTable.1に示す。また,実電力負荷は図中点線で囲まれているターボ冷凍機への電気入力と電力負荷の和となる。
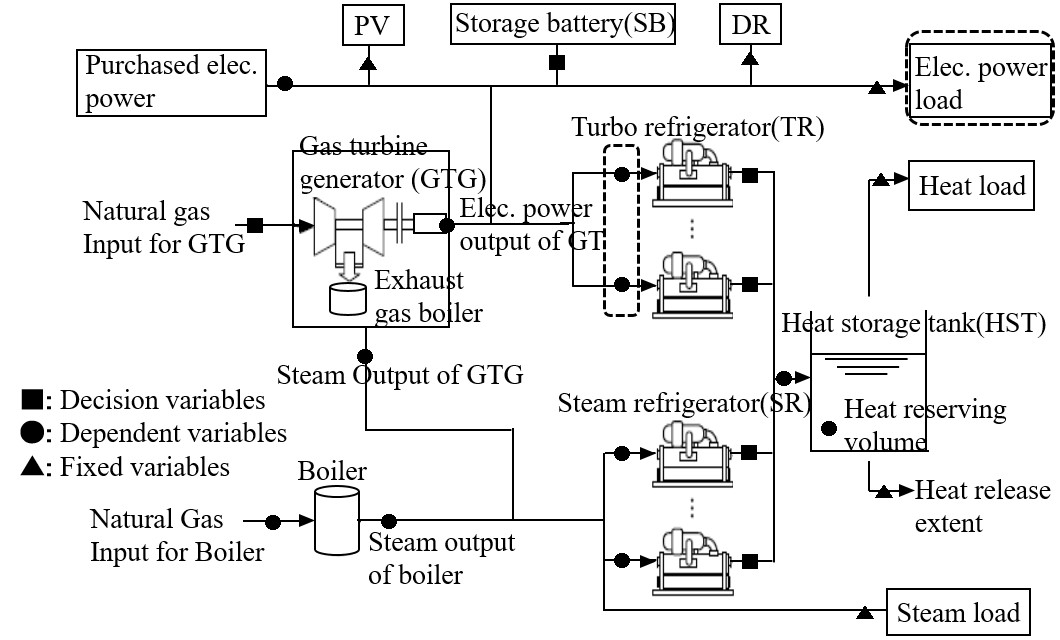
Fig. 2 産業モデル概要図(2)
表1 産業モデルの設備特性
| 設備特性 | 下限値 | 上限値 | |
|---|---|---|---|
| ガスタービンによる電力出力量(a) | - | 6[MW/h] | 20[MW/h] |
| ガスタービンへの燃料入力量(b) | 線形(入力:(a)) | 1103.68[m3/h] | 3678.93 [m3h] |
| ガスタービンによる蒸気出力量(c) | 線形(入力:(b)) | 2.99 [Ton/h] | 9.97[Ton/h] |
| ボイラーへの燃料入力量(d) | 線形(入力:(e)) | 0[m3/h] | 804.02[m3/h] |
| ボイラーによる蒸気出力量(e) | 線形(入力:(b),(h)) | 0 [Ton/h] | 16 [Ton/h] |
| ターボ冷凍機への電力入力量(f) | 線形(入力:(g)) | 0.07[MW/h] | 0.23[MW/h] |
| ターボ冷凍機による熱出力(g) | - | 1.5[GJ] | 5.0[GJ] |
| 蒸気吸収式冷凍機への蒸気入力量(h) | 線形(入力:(i)) | 0.79[Ton/h] | 2.63[Ton/h] |
| 蒸気吸収式冷凍機による熱出力(i) | - | 5[GJ] | 15[GJ] |
| 蓄熱層への熱入力量(j) | =(g)+(i) | - | - |
| 蓄熱層からの熱出力量(k) | =熱負荷 | - | - |
| 蓄熱量(l) | - | 0[GJ] | 500[GJ] |
| 蓄電池への電力入力量(m) | - | 0[MW] | 2[MW] |
| 蓄電池からの電力出力量(n) | - | 0[MW] | 2[MW] |
| 蓄電量(o) | 初期値=24時蓄電量 | 2.4[MW] | 12[MW] |
| 購入電力量(p) | =(b)+(d) | 0[m3/h] | - |
| 購入ガス量(q) | =実電力負荷+(f)-(a)+(m)-(n) | 0[MW] | - |
(2)業務分野モデル(2)
業務分野のモデル概要図をFig. 3に示す。図中に,決定変数(■),従属変数(●),定数(▲)を示す。産業分野では電力,蒸気,熱エネルギーを扱う。Fig. 3の,各時間帯の電力,蒸気,熱のバランスについては,システム構成図の各々のエネルギー毎の接続状態により決定される。 Fig. 3の各設備の特性をTable. 2に示す。また,実電力負荷は図中点線で囲まれたターボ冷凍機への電気入力と電力負荷の和である。
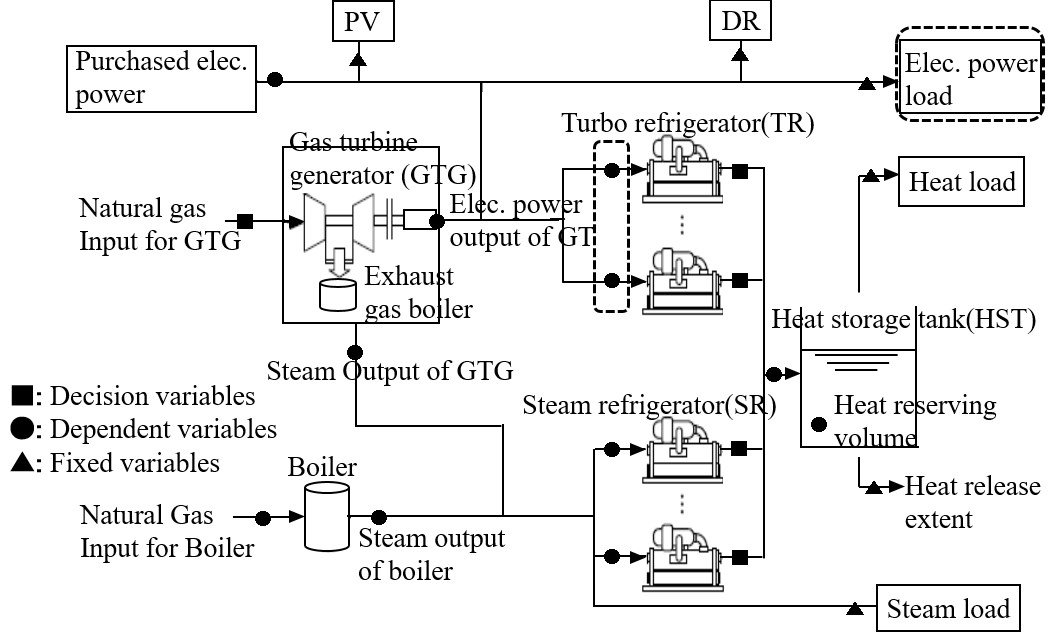
Fig.3 業務モデル概要図(2)
表2 業務モデルの設備特性
| 設備特性 | 下限値 | 上限値 | |
|---|---|---|---|
| ガスタービンによる電力出力量(a) | - | 6[MW/h] | 20[MW/h] |
| ガスタービンへの燃料入力量(b) | 線形(入力:(a)) | 1103.68[m3/h] | 3678.93 [m3h] |
| ガスタービンによる蒸気出力量(c) | 線形(入力:(b)) | 2.99 [Ton/h] | 9.97[Ton/h] |
| ボイラーへの燃料入力量(d) | 線形(入力:(e)) | 0[m3/h] | 804.02[m3/h] |
| ボイラーによる蒸気出力量(e) | 線形(入力:(b),(h)) | 0 [Ton/h] | 16 [Ton/h] |
| ターボ冷凍機への電力入力量(f) | 線形(入力:(g)) | 0.07[MW/h] | 0.23[MW/h] |
| ターボ冷凍機による熱出力(g) | - | 1.5[GJ] | 5.0[GJ] |
| 蒸気吸収式冷凍機への蒸気入力量(h) | 線形(入力:(i)) | 0.79[Ton/h] | 2.63[Ton/h] |
| 蒸気吸収式冷凍機による熱出力(i) | - | 5[GJ] | 15[GJ] |
| 蓄熱層への熱入力量(j) | =(g)+(i) | - | - |
| 蓄熱層からの熱出力量(k) | =熱負荷 | - | - |
| 蓄熱量(l) | - | 0[GJ] | 500[GJ] |
| 購入電力量(p) | =(b)+(d) | 0[m3/h] | - |
| 購入ガス量(q) | =実電力負荷+(f)-(a) | 0[MW] | - |
(3)家庭分野モデル(2)
家庭分野のモデル概要図をFig. 4に示す。図中に,決定変数(■),従属変数(●),定数(▲)を示す。家庭分野では電力,蒸気,熱エネルギーを扱う。Fig. 4では,各時間帯の電力,蒸気,熱のバランスについて,システム構成図の各々のエネルギー毎の接続状態により決定される。Fig. 3の各設備の特性をTable. 3に示す。また,実電力負荷は図中点線で囲んだ電力負荷とエコキュートへの電気入力の和である。
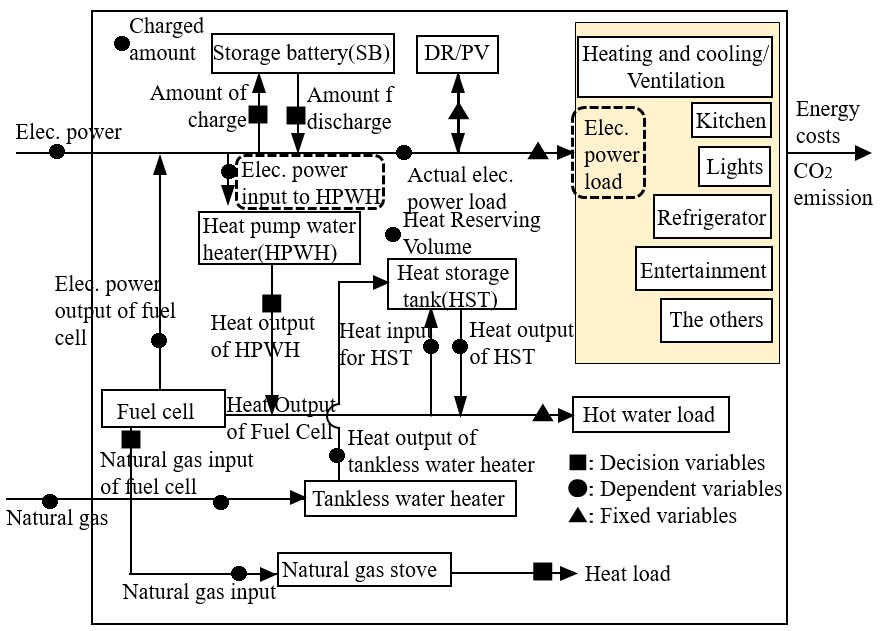
Fig.4 家庭モデルの概要図(2)
表3 家庭モデルの設備特性
| 設備特性 | 下限値 | 上限値 | |
|---|---|---|---|
| 燃料電池による電力出力量(a) | - | 0.2[kW/h] | 0.75[kW/h] |
| 燃料電池への燃料入力量(b) | 線形(入力:(a)) | 0.05[m3/h] | 0.17 [m3h] |
| 燃料電池による熱出力量(c) | 線形(入力:(b)) | 1.03[MJ] | 3.88[MJ] |
| エコキュートへの電力入力量(d) | 非線形(入力:(g)) | 0[kWh] | 4.53[kWh] |
| エコキュートによる熱出力量(e) | 0 [MJ] | 46 [MJ] | |
| ガスコンロへの入力ガス量(f) | 線形(入力:(g)) | 0.07[MW/h] | 0.23[MW/h] |
| ガスコンロからの熱出力(g) | =熱負荷 | 0[Mh] | 5.0[GJ] |
| 給湯機への燃料入力量(h) | 非線形(入力:(l)) | 0.79[Ton/h] | 2.63[Ton/h] |
| 給湯機からの熱出力量(i) | 線形(入力:(h)) | 5[GJ] | 15[GJ] |
| 蓄熱層への熱入力量(j) | 非線形(入力:(c),(e)) | - | - |
| 蓄熱層からの熱出力量(k) | =熱負荷 | - | - |
| 蓄熱量(l) | 線形 (入力:(m),(n),(i)) |
0[kWh] | 500[kWh] |
| 蓄電池への電力入力量(m) | - | 0[kWh] | 0.83[kWh] |
| 蓄電池からの電力出力量(n) | - | 0[kWh] | 0.83[kWh] |
| 蓄電量(o) | 初期値=24時蓄電量 | 1[Wh] | 5[Wh] |
| 購入電力量(p) | =(b)+(d) | 0[m3/h] | - |
| 購入ガス量(q) | =実電力負荷+(a)+(d)+(m)-(n) | 0[MW] | - |
(4)鉄道分野モデル(3,4)
鉄道分野については,文献(3) (4)を利用してモデルが作成された。このモデルでは,決定変数は,平均乗車距離,乗車人数,エネルギー消費原,編成車両,車両定員,時間平均速度,平均運行距離,運行本数となっている。従属変数や定数,設備特性は文献(3)(4)を参照していただきたい。
(5)上水道分野モデル(5)
上水道分野のモデル概要図をFig. 5に示す。図中に,決定変数(■),従属変数(●),定数(▲)を示す。上水道分野では電力,蒸気,熱エネルギーを扱う。Fig. 5において,各時間帯の電力,蒸気,熱のバランスについては,システム構成図の各々のエネルギー毎の接続状態により決定される。Fig. 5の各設備の特性をTable. 4示す。
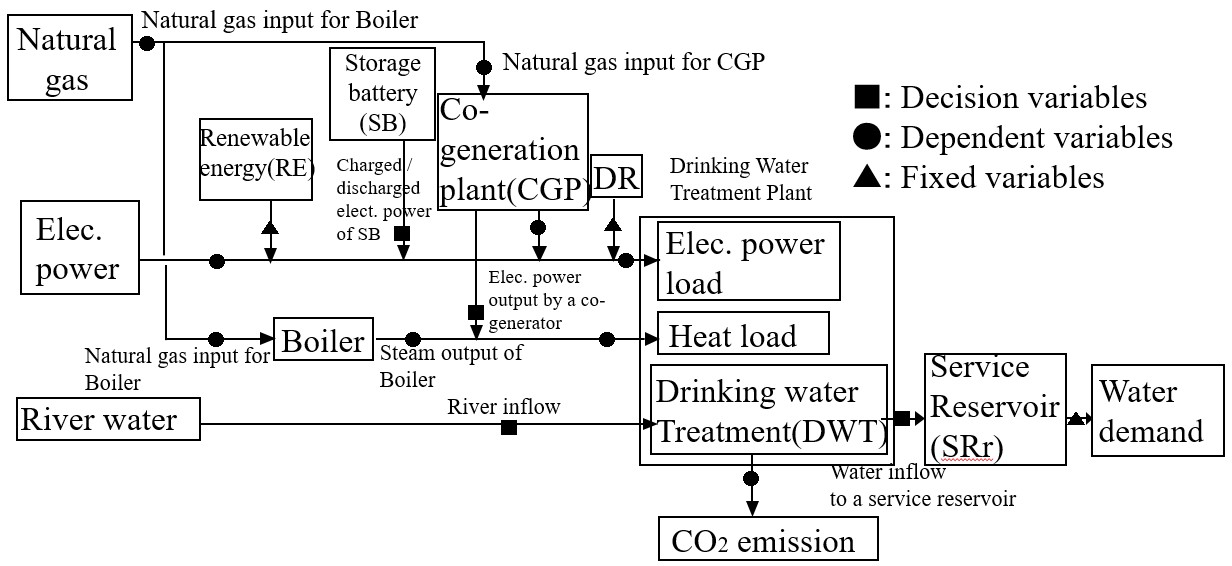
図5 上水モデルの概要図(5)
表4上水モデルの設備特性
| 設備特性 | 下限値 | 上限値 | |
|---|---|---|---|
| 河川の流入量(a) | - | 0[m3] | ー |
| 取水・上水施設への流入量(b) | - | 0[m3] | ー |
| 上水池の貯留量(c) | - | 7000[m3] | 60000[m3] |
| 配水池の貯留量(d) | - | 7000[m3] | 60000[m3] |
| 電力負荷(e) | 線形(入力:(a),(b)) | - | - |
| 実電力負荷(f) | =(e)-DR-RE | - | - |
| 熱負荷(g) | 線形(入力:(a)) | - | - |
| コジェネ発電機による電力出力量(h) | - | 0.10[MW/h] | 2.00[MW/h] |
| コジェネ発電機への燃料入力量(i) | 線形(入力:(h)) | 50.00[m3/h] | 296.30 [m3h] |
| コジェネ発電機による熱出力量(j) | 線形(入力:(i)) | 0.81 [MJ] | 4.80[MJ] |
| ボイラーへの燃料入力量(k) | 線形(入力:(l)) | 0[m3/h] | 804.02[m3/h] |
| ボイラーからの蒸気出力量(l) | 線形(入力:(g),(ji)) | 0 [Ton/h] | 16 [Ton/h] |
| 蓄電池への電力入力量(m) | - | 0[kWh] | 0.08[kWh] |
| 蓄電池からの電力出力量(n) | - | 0[kWh] | 0.08[kWh] |
| 蓄電量(o) | 初期値=24時蓄電量 | 0.2[Wh] | 1[Wh] |
| 購入電力量(p) | =(i)+(k) | 0[m3/h] | - |
| 購入ガス量(q) | =(f)-(h)+(m)-(n) | 0[MW] | - |
(6)下水道分野モデル(5)
下水道分野のモデルをFig. 6に示す。図中に,決定変数(■),従属変数(●),定数(▲)を示す。Fig. 6において,各時間帯の電力,蒸気,熱のバランスについては,システム構成図の各々のエネルギー毎の接続状態により決定できる。Fig. 6の各設備の特性をTable. 5にあげる。
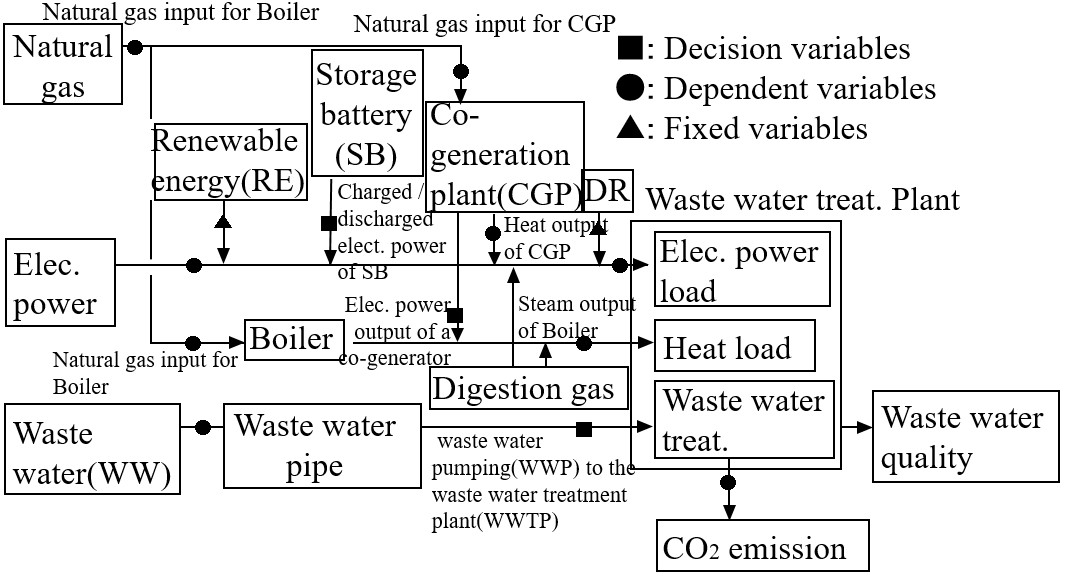
図6 下水モデル概要図(5)
表5 下水モデルの設備特性
| 設備特性 | 下限値 | 上限値 | |
|---|---|---|---|
| 下水管への下水流入量(a) | - | 0[m3] | ー |
| 下水管での下水貯留量(b) | 線形(入力:(a)) | 7000[m3] | 60000[m3] |
| 電力負荷(c) | 線形(入力:(a)) | - | - |
| 実電力負荷(d) | =(c)-DR-RE | - | - |
| 熱負荷(e) | 線形(入力:(a)) | - | - |
| コジェネ発電機による電力出力量(f) | - | 0.10[MW/h] | 2.00[MW/h] |
| コジェネ発電機への燃料入力量(g) | 線形(入力:(h)) | 50.00[m3/h] | 296.30 [m3h] |
| コジェネ発電機による熱出力量(h) | 線形(入力:(i)) | 0.81 [MJ] | 4.80[MJ] |
| ボイラーへの燃料入力量(i) | 線形(入力:(l)) | 0[m3/h] | 804.02[m3/h] |
| ボイラーからの蒸気出力量(j) | 線形(入力:(g),(ji)) | 0 [Ton/h] | 16 [Ton/h] |
| 蓄電池への電力入力量(k) | - | 0[kWh] | 0.08[kWh] |
| 蓄電池からの電力出力量(l) | - | 0[kWh] | 0.08[kWh] |
| 蓄電量(m) | 初期値=24時蓄電量 | 0.2[Wh] | 1[Wh] |
| 購入電力量(n) | =(g)+(i) | 0[m3/h] | - |
| 購入ガス量(o) | =(d)-(f)+(k)-(l) | 0[MW] | - |
参考文献
(1) 安田恵一郎:「スマートコミュニティの定義とモデル構築」,電気学会全国大会,1-H1-2 (2015)
(2) 松井哲郎・他:「スマートコミュニティにおけるエネルギー需要モデル」,電気学会全国大会,1-H1-4 (2015)
(3) 近藤稔・小川知行・村上浩一:「鉄道車両の消費エネルギー簡易計算法」, 鉄道総研報告 Vol.25, No.8, pp41-46 (2011-8)
(4) 国交省:「鉄道プロジェクトの評価手法マニュアル(2012年改訂版)」 http://www.mlit.go.jp/tetudo/tetudo_fr1_000040.html (2012)
(5) 山口順之・他:「スマートコミュニティにおけるエネルギー供給モデル」,電気学会全国大会,1-H1-3 (2015)